OGL_ISS - International Space Station in Danger

Inhalt

• 1. Vorspiel
  • 1.1. Was einen halt so wurmt
  • 1.2. Deep Coding in the Sky
  • 1.3. Meine eigene ISS muss her
• 2. Aufbau von "OGL_ISS"
  • 2.1. Unit "DanGeoU.pas" - der Mathe-Refresh
    • 2.1.1. Konstanten und Typen
    • 2.1.2. Winkel in Grad und Bogenmass
    • 2.1.3. Vektor-Operationen
      • 2.1.3.1. Addition und Subtraktion von Vektor
      • 2.1.3.2. Länge eines Vektors
      • 2.1.3.3. Winkel zwischen Vektoren
      • 2.1.3.4. Vektor-Kreuz-Produkt
      • 2.1.3.5. Was haben Sinus und Kosinus mit Vektoren zu schaffen?
      • 2.1.3.6. Distanz zwischen Vektoren
    • 2.1.4. Matrizen-Operationen
      • 2.1.4.1. Achsen-Rotationsmatrizen
      • 2.1.4.2. Multiplikation von Matrizen
      • 2.1.4.3. Multiplikation von Matrizen mit Vektoren
  • 2.2. Unit "SoundsU.pas" - nie wieder Ressourcen-Editor
    • 2.2.1. TImage-Komponente für Bilder in der Applikation
    • 2.2.2. Doch was ist mit Sounds?
    • 2.2.3. Bytes sind Bytes sind Bytes
    • 2.2.4. Eine eigene Unit nur für Sounds
  • 2.3. Unit "HauptU.pas" - All in one
• 3. Programmierung von "OGL_ISS"
  • 3.1. Alle nötigen Units
  • 3.2. Konstanten und Variablen
  • 3.3. Form-Zeugs
    • 3.3.1. Erzeugung
    • 3.3.2. WAV-Arrays in die Boxen gedrückt
    • 3.3.3. Designarbeiten
    • 3.3.4. Form-Zerstörung
  • 3.4. Objekte und Texturen initialisieren
    • 3.4.1. Objekte
      • 3.4.1.1. Weltallkugel
      • 3.4.1.2. Erdkugel
      • 3.4.1.3. ISS
      • 3.4.1.4. Meteore
    • 3.4.2. Texturen
      • 3.4.2.1. Bilder über spezielle OpenGL-DLLs
      • 3.4.2.2. Bilder ohne DLLs und Plattenzugriffe
  • 3.5. Programm-Taktung: Timer-gesteuerte Action
    • 3.5.1. Computer sind verschieden
    • 3.5.2. Timer- statt OnIdle-Ereignisse
      • 3.5.2.1. Zähler-Update
      • 3.5.2.2. User-Eingaben-Check
      • 3.5.2.3. Kalkulation von Rotations- und Positions-Delta
      • 3.5.2.4. Cockpit-Update
  • 3.6. Fliegen im dreidimensionalem Raum
    • 3.6.1. Probleme mit der Fadenkreuz-Navigation
    • 3.6.2. Positionsänderung
    • 3.6.3. Richtungsänderung
    • 3.6.4. Hilfe durch Rotations-Matrizen
  • 3.7. Spiel-Auswahl
    • 3.7.1. Die Qual der Wahl
      • 3.7.1.1. Level-Auswahl
      • 3.7.1.2. Taktfrequenz-Auswahl
    • 3.7.2. Wenn der User drückt - Tastatur-Ereignisse abfangen
  • 3.8. Spiel-Start
    • 3.8.1. Programm-Parameter setzen
    • 3.8.2. Meteore verteilen
  • 3.9. Spiel-Ablauf
    • 3.9.1. Szenen-Rendering
      • 3.9.1.1. Acht Grafik-Modi
      • 3.9.1.2. Wo sind wir im Modell?
      • 3.9.1.3. Der Welten-Raum wird gemalt
      • 3.9.1.4. Die Erde wird gemalt - Home, sweet home
      • 3.9.1.5. Die ISS wird zusammengebaut
    • 3.9.2. Meteor-Handling
      • 3.9.2.1. Platzierung der Killer-Meteore
      • 3.9.2.2. Ballerei - Linie trifft Sphäre
      • 3.9.2.3. Schuss-Salven
    • 3.9.3. Spurensuche
    • 3.9.4. Den Feind ins Visier genommen
    • 3.9.5. Automatischer Heimflug
  • 3.10. Spiel-Ende
• 4. Spiel-Impressionen
• 5. Träume werden wahr
• 6. Download

1. Vorspiel

1.1. Was einen halt so wurmt

Ihr erinnert euch? Beim "OGL_Planets"-Tutorial habe ich bedauert, dass es angesichts der gewaltigen Dimensionen des Sonnensystems nicht möglich war, Objekte darzustellen, deren Ausmasse kleiner als einen Kubikkilometer sind. Denn damit kam der verflixte Tiefenpuffer von OpenGL nicht zurecht. Solche Objekte verschwanden einfach, wenn man sich ihnen zu weit näherte.

Das war schade. Denn gerne hätte ich der Erde neben dem Mond noch einen weiteren Trabanten gegönnt, nämlich die ISS. Klein und unscheinbar sollte sie dort als der entfernteste Aussenposten der Menschheit still ihre Kreise ziehen.

Echt ärgerlich, dass das nicht geklappt hat. Wo sie doch so schön anzuschauen ist:

Raumstation im Erdorbit: Die ISS im Juni 2008, aufgenommen aus dem Space Shuttle Discovery.
Quelle: Deutsche Wikipedia.

1.2. Deep Coding in the Sky

Zum Glück muss man als Programmierer mit solchem Ärger nicht leben. Wenn es eine ISS sein soll, dann bastelt man sich halt eine. Dazu musste nur der innere Schweinehund überwunden werden.

Wachte dann mal wieder zu früh auf, so um 6 Uhr herum. Passiert mir im Sommer öfter. An Schlaf war nicht mehr zu denken. Und noch zwei elend lange Stunden Zeit, bevor es zur Arbeit ging. Also, was tun?

Wie üblich gab es Kaffee, Kippen und Platzierung am PC. Das Ding habe ich mir "um" mein Zweit-Bett gebaut, was kuschelig-gemütliches Programmieren ermöglicht.

Daniels Home-PC: Kaffee, Zigaretten, Bett, Computer und ewig flimmernder Monitor. Hier lässt es sich gemütlich, aber intensiv und störungsfrei arbeiten.

Es ging online. Zu Wikipedia. Zufällige Artikel. Und landete so beim Lemma Internationale Raumstation.

Die ISS. Da ist sie wieder. Da war doch noch was ...

1.3. Meine eigene ISS muss her

Die Kombination aus Erinnerung, neuen Informationen, PC und zu viel Zeit liess mich ein neues Projekt in Delphi beginnen.

Bis es zur Arbeit ging, war die Erde weitgehend fertig. Die ISS eine simple Sphäre. Eine Flugsteuerung noch nicht vorhanden.

Drei Tage später konnte man sich bereits virtuell durch die verschiedenen, 345 km über dem Erdboden schwebenden, Module meiner Raumstation bewegen.

Noch einmal fünf Tage später war die Fliegerei im 3-dimensionalen Raum hinreichend optimiert und alle Elemente mit Texturen versehen.

Nur Herumfliegen und -gucken war aber langweilig. Also wurde ein Spiel eingebaut. Mit Phaserfeuer, Explosionen, Soundeffekten, Level und Highscore-Listen.

Nach zwei Wochen Programmierrausch war die Sache dann gegessen.

Jetzt fehlte nur noch das obligatorische Tutorial ...

2. Aufbau von "OGL_ISS"

Wie schon "OGL_Henrys" und "OGL_Planets" wurde "OGL_ISS" in DelphiGL programmiert.

Das Projekt besteht aus drei Units:

1. DanGeoU.pas: Funktionssammlung zur Vektor- und Matrizen-Verwaltung
2. SoundsU.pas: const-Arrays mit den WAV-Daten für die Sound-Effekte
3. HauptU.pas: Eigentlicher Programm-Code von "OGL_ISS"

2.1. Unit "DanGeoU.pas" - der Mathe-Refresh

Trotz mehrerer OpenGL-Programme auf dem Kerbholz habe ich mich stets gekonnt vor der Mathematik dahinter gedrückt.

Das war bei "OGL_ISS" leider nicht drin. Punktgenaues Navigieren in 3D ohne etwas Ahnung von Trigonometrie ist ... frustrierend. Da kommt man einfach nicht vom Fleck. Ich weiss es genau, denn ich habe Tage damit verschwendet, durch wüstes Trial-and-Error mit Sinus- und Kosinus-Kombinationen irgendetwas Sinnvolles hinzubekommen.

Also hiess es hinsetzen und lernen. Was ist ein Vektor? Was bringen mir Matrizen? Kann ich die für Rotationen einsetzen? Es entstand eine kleine Sammlung von Typen und Funktionen, die in der Unit "DanGeoU.pas" verpackt wurde.

2.1.1. Konstanten und Typen

Fangen wir mit den Konstanten und Typen an:

2.1.2. Winkel in Grad und Bogenmass

Winkel lassen sich bekanntlich in Grad und im Bogenmass angeben.

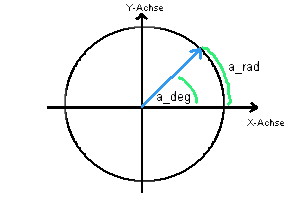
Winkelmasse: Winkel lassen sich im Grad- und Bogenmass angeben. Ein Mass lässt sich aber jederzeit leicht in das andere Mass umrechnen.

Bogenmass-Winkel repräsentieren Längen von Einheitskreisabschnitten. Sie sind mathematisch einfacher zu bearbeiten als Grad-Winkel, da hier keine "künstlichen Grenzwerte" wie etwa der 360 Grad-Winkel berücksichtigt werden müssen.

Das dürfte auch der Grund sein, weshalb bei den meisten OpenGL-Funktionen Bogenmass-Winkel als Parameter erwartet werden. Gleiches gilt für die "DanGeoU.pas". Sollte eine Prozedur dennoch Grad-Winkel erwarten, dann verfügt sie über das Postfix "_deg" im Funktionsnamen.

Mit Hilfe der Konstanten "_rad2deg" und "_deg2rad" können Winkel leicht von einem Format in das andere umgerechnet werden:

2.1.3. Vektor-Operationen

Der Typ "Tv" beschreibt Vektoren. Einen Vektor kann man als Punkt im n-dimensionalen Raum interpretieren oder als ein vom Ursprung ausgehender Pfeil, der eine Richtung besitzt.

Die Vektoren, die in der "DanGeoU.pas" Verwendung finden, gelten ausschliesslich für n=3, also den 3-dimensionalen Raum mit den Achsen X, Y und Z:

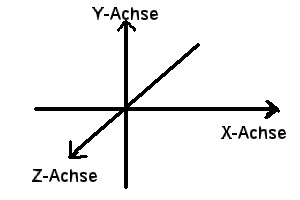
Die x-/y-/z-Achsen des OpenGL-Raumes: Man beachte hierbei, dass die z-Achse bei OpenGL auf den Beobachter hin ausgerichtet ist (anders als bei Direct3D). Will man also einen Punkt tiefer in den Raum hinein wandern lassen, muss der z-Wert der Koordinaten negiert vergrössert werden.

Intern arbeitet OpenGL mit 4-dimensionalen Vektoren, wobei die vierte Dimension, die w-Achse, etwas mit der Projektion des Ergebnisses auf dem Monitor zu tun hat, und uns hier nicht weiter interessieren muss.

Auf Vektoren lassen sich verschiedene, wohldefinierte Operationen anwenden.

2.1.3.1. Addition und Subtraktion von Vektor

Beginnen wir mit Plus und Minus:

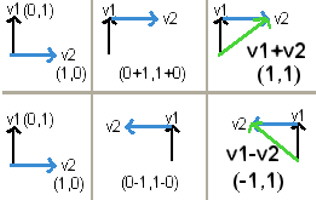
Addition und Subtraktion von Vektoren: Geometrische Veranschaulichung der Wirkung von Addition (oben) und Subtraktion (unten) von Vektoren, hier zum leichteren Verständnis nur im zweidimensionalen Raum wiedergegeben.

2.1.3.2. Länge eines Vektors

Die Länge eines Vektors (oder auch sein Betrag) lässt sich mithilfe des Satzes von Pythagoras ermitteln:

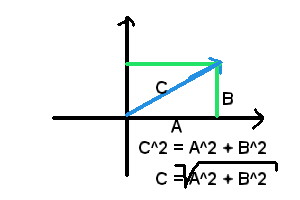
Länge eines Vektors: Die Länge eines Vektors lässt sich mithilfe des Satzes von Pythagoras ermitteln. Der Vektor fungiert dabei als Hypotenuse eines gleichschenkligen Dreiecks.

Teilt man die Werte eines Vektors durch seine Länge, erhält man den auf den Einheitskreis normierten Vektor. Das ist nützlich, wenn nur die Richtung eines Vektors interessiert, nicht aber seine Position im Raum.

Um einen Vektor in gegebener Richtung zu verlängern, zu verkürzen oder zu negieren bietet sich die Skalierung an:

2.1.3.3. Winkel zwischen Vektoren

Den Winkel zwischen zwei Vektoren findet man mithilfe der Vektor-Länge (siehe weiter oben), dem Vektor-Punkt-Produkt und einer schicken kleinen Formel:

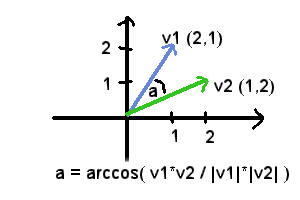
Winkel zwischen zwei Vektoren	Punktprodukt=  (v1.x*v2.x+v1.y*v2.y)=  (1*2+2*1)=  4 Länge v1=  wurzel(v1.x*v1.x+v1.y*v1.y)=  wurzel(2*2+1*1)=  wurzel(5) Länge v2=v1 Winkel a =  arcos( 4/(wurzel(5)*wurzel(5)) )=  arcos( 4/5 ) ~  36.8 Grad

2.1.3.4. Vektor-Kreuz-Produkt

Das Vektor-Kreuz-Produkt ist hilfreich, um die Senkrechte einer Fläche zu ermitteln, die durch zwei Vektoren aufgespannt wird. Die Rechte-Hand-Regel zeigt uns, in welche Richtung die resultierende Senkrechte weisen wird. Es gilt:

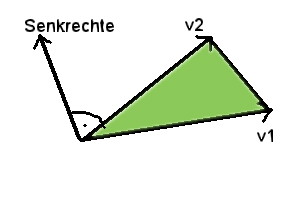
Vektor-Kreuz-Produkt: Mithilfe des Vektor-Kreuz-Produkts kann die Senkrechte der durch zwei Vektoren aufgespannten Fläche im dreidimensionalen Raum berechnet werden.	Zeigefinger in v1-Richtung Mittelfinger in v2-Richtung Daumen ergibt Senkrechte

Für die Rotation eines Vektors um die Achsen des 3-dimensionalen Raumes gelten die folgenden Formeln:

2.1.3.5. Was haben Sinus und Kosinus mit Vektoren zu schaffen?

Wie erklären sich diese Formeln? Wie kommen zum Beispiel all die Sinus- und Kosinus-Werte in die Berechnungen?

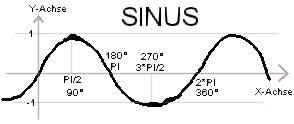
Sinus-Kurve: Die trigonometrische Sinus-Funktion durchläuft den Ursprung bei 0 und hat ihre Minima und Maxima jeweils bei Vielfachen von PI/2.

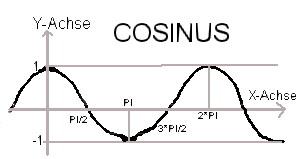
Kosinus-Kurve: Die trigonometrische Kosinus-Funktion durchläuft den Ursprung bei 1 und hat ihre Minima und Maxima jeweils bei Vielfachen von PI.

Die Trigonometrie lehrt uns folgenden Zusammenhang zwischen den y- und y-Koordinaten, wenn ein Vektor um die z-Achse mit dem Winkel "a" rotiert wird:

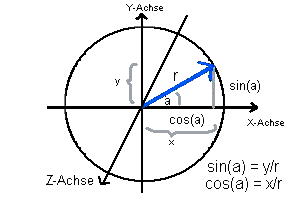
Rotation eines Vektors um die z-Achse: Wird ein Vektor (x/y) um die z-Achse rotiert, dann ergeben sich die neuen Koordinaten anhand einer Kombination aus Radius (Vektorlänge), Sinus und Kosinus.

Wird nun der Winkel "a" um einen Winkel "b" ergänzt, dann gilt für die neuen Koordinaten "xneu" und "yneu":

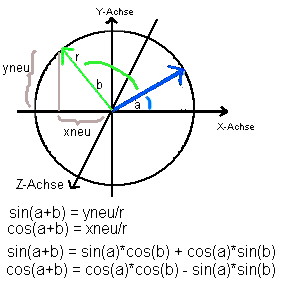
Erweiterte Rotation eines Vektors um die z-Achse: Wird ein Vektor /x/y) um die Winkel 'a' und 'b' rotiert, dann können die neuen Koordinaten (xneu/yneu) mittels einer Formel berechnet werden.

Damit lässt sich nach "xneu" und "yneu" auflösen:

Entsprechend kann für die Rotationen um die x- und y-Achse verfahren werden.

Zu beachten ist, dass die Reihenfolge der Rotationen nicht einerlei ist. Es dauerte eine Weile, bis mir das klar war. Die folgenden 90 Grad-Rotationen um verschiedenen Achsen mögen dies illustrieren:

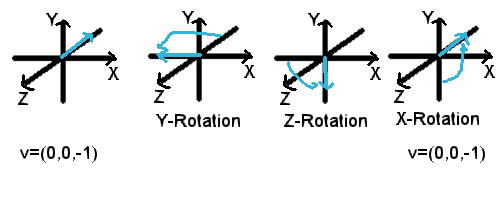
Vektorrotation um die Achsen y, z und x: Rotiert man einen Vektor mit jeweils 90 Grad in der Reihenfolge y-, z- und x-Achse, dann weist der Vektor letztlich wieder in die ursprüngliche Richtung.

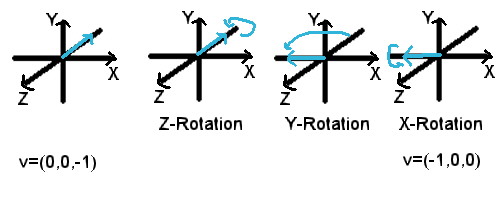
Vektorrotation um die Achsen z, y und x: Rotiert man einen Vektor dagegen mit jeweils 90 Grad in der Reihenfolge z-, y- und x-Achse, dann weist der Vektor in eine andere Richtung als der ursprüngliche Vektor.

2.1.3.6. Distanz zwischen Vektoren

Um die Distanz zwischen zwei "Punkt"-Vektoren zu ermitteln, hilft einmal mehr der Satz von Pythagoras:

Weil das Rechnen mit Sinus und Kosinus irrationale Zahlen hervorbringt, bleiben Rundungsfehler nicht aus. Werte, die mathematisch eigentlich exakt null sein sollten, behalten dann häufig einen Restwert. Um den Ursprungs-Vektor (0,0,0) trotz enthaltener Restwerte identifizieren zu können, wurde die Prüfungsfunktion "v_iszero" mit Toleranz-Parameter implementiert:

2.1.4. Matrizen-Operationen

Der Typ "Tm" beschreibt eine 3 x 3 Matrix. Matrizen werden in OpenGL verwendet, um Vektoren auf elegante Weise zu rotieren und zu verschieben (dort werden jedoch aufgrund der w-Dimension 4 x 4 Matrizen eingesetzt).

Die folgende Funktion zur Erzeugung einer Einheitsmatrix zeigt, wie die Matrizen in der "DanGeoU.pas" aufgebaut sind:

Für eine Einheitsmatrix gilt im Übrigen, dass sie, multipliziert mit einem Vektor, diesen unverändert lässt.

Mit Nullen füllen kann man die "Tm"-Matrix über die Funktion "m_clr":

In "OGL_ISS" benötigen wir Matrizen zur Achsen-Rotation.

Matrizen haben den Vorteil, dass man sie miteinander multiplizieren kann, wobei ihre Rotationseigenschaften erhalten bleiben. Auf diese Weise lässt sich eine generalisierte Rotationsmatrix bilden, die einen Vektor mit nur einer Multiplikation um alle drei Achsen rotiert.

2.1.4.1. Achsen-Rotationsmatrizen

Die einzelnen Achsen-Rotationsmatrizen sind:

2.1.4.2. Multiplikation von Matrizen

Zwei "Tm"-Matrizen multipliziert man folgendermassen:

2.1.4.3. Multiplikation von Matrizen mit Vektoren

Und zuletzt haben wir noch die Multiplikation einer "Tm"-Matrix mit einem "Tv"-Vektor:

2.2. Unit "SoundsU.pas" - nie wieder Ressourcen-Editor

2.2.1. TImage-Komponente für Bilder in der Applikation

Um (JPG-)Bilder in ein Delphi-Programm zu integrieren, genügt es, sie mittels TImage im Objektinspektor einzuladen. Kompiliert man dann das Projekt, sind die Daten des Bildes im laufenden Programm direkt verfügbar, müssen also nicht erst von der Festplatte nachgeladen werden.

2.2.2. Doch was ist mit Sounds?

Leider existiert keine Klasse TSound, mit der man Gleiches für WAV-Daten realisieren könnte. Üblicherweise muss daher der Delphi-eigene Ressourcen-Editor bemüht werden, um WAV-Daten in eine EXE-Datei integrieren zu können.

2.2.3. Bytes sind Bytes sind Bytes

Da dieses Verfahren recht kompliziert ist, habe ich mir ein kleines Tool namens "File2Array" geschrieben, welches eine beliebige Datei ausliest und als konstantes Delphi-Array wiedergibt. Diese Daten können dann einfach in eine Unit kopiert und wie normaler Source kompiliert werden.

Folgendes Beispiel soll dies demonstrieren:

Wir haben die Text-Datei "hallo.txt" auf Festplatte gespeichert:

Daraus macht dann "File2Array.exe" folgende Text-Datei:

Da unter Windows letztlich alle Daten eine Folge von Bytes sind, funktioniert diese Methode mit jeder Art von Datei, egal, ob sie nun Bilder, Sounds, Texte oder Filme enthält.

2.2.4. Eine eigene Unit nur für Sounds

Auch wenn es eigentlich nicht nötig ist, wurden die drei so generierten WAV-Datenströme bei "OGL_ISS" in eine eigene Unit "SoundsU.pas" gelegt. Das Ganze sieht dann in etwa so aus:

Wie wir letztlich diese Array-Daten im Programm nutzen können, sehen wir gleich noch.

2.3. Unit "HauptU.pas" - All in one

Der eigentliche Programm-Code von "OGL_ISS" befindet sich komplett in der Unit "HauptU.pas". Schöner wäre es wohl gewesen, mehrere Units zu verwenden, etwa eine für die Steuerung, eine für die Spielfunktionen und eine für das Rendern. Jedoch ist der Quellcode insgesamt so knapp ausgefallen, dass das gar nicht nötig war.

Die Applikation begnügt sich zudem mit nur einer TForm, auf der sich alles abspielt. Hier ein Screenshot der "hauptf":

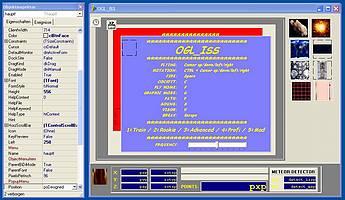
Delphi-Form 'thauptf': Die Hauptform von 'OpenGL ISS'. Hier spielt sich alles ab. Edits, Bildcontainer, Panels, Labels, Timer und alles Restliche, was zur Anzeige nötig ist.

3. Programmierung von "OGL_ISS"

3.1. Alle nötigen Units

Die in das Projekt eingebundenen Units sind:

Neben den Standard-Units gibt es "XPMan" (XPManifest) für die schönere Optik, "Math" für trigonometrische Funktionen, "JPEG" für JPG-Bilder, "IniFiles" für Konfigurationsdateien und "MMSystem" für die Sound-API.

Die OpenGL-Funktionalität wird über "DGLOpenGL" eingebunden. Anders als bei meinen vorherigen OpenGL-Projekten werden die Units "SDL" und "SDL_Image" hier nicht benötigt.

Zuletzt werden dann noch meine eigenen, weiter oben beschriebenen Units "DanGeoU" und "SoundsU" hinzugefügt.

3.2. Konstanten und Variablen

Die verwendeten Konstanten, Typen und "globalen" Variablen sind:

Eine Erläuterung erspare ich mir. Die Liste dient nur als Referenz-Liste, wenn bei der Source-Beschreibung weiter unten diese Bezeichner auftauchen.

3.3. Form-Zeugs

3.3.1. Erzeugung

Wie bei Delphi üblich, wird nach dem Programmstart automatisch die Prozedur "FormCreate" aufgerufen:

Schauen wir uns mal an, was bei dieser Prozedur so alles passiert.

3.3.2. WAV-Arrays in die Boxen gedrückt

Zu Beginn werden die konstanten WAV-Arrays aus der "SoundsU.pas" in TMemoryStream-Objekte eingelesen. Diese lassen sich später an die Prozedur "dosound" übergeben, wo sie letztlich über die API-Funktion "sndPlaySound" abgespielt werden:

"sound_c" ist ein Zähler, der angibt, wie lange (das heisst, wie viele "Zeiteinheiten") ein Sound mindestens abgespielt wird, bevor er durch einen anderen ersetzt werden darf. Für Multi-Sound-Effekte hätte ich mich sonst mit der DirectSound-API herumschlagen müssen - und dann wäre der Source gewiss umfangreicher ausgefallen.

3.3.3. Designarbeiten

Anschliessend werden alle TComponents der TForm "hauptf" durchlaufen und nach TPanels durchsucht. Wird ein TPanel gefunden, so wird es u.a. schwarz eingefärbt und die Eigenschaft "parentbackground" wird auf "false" gesetzt. Das ist notwendig wegen eines lästigen Bugs des XP-Manifests - ohne diese Korrektur "merkt" sich TPanel sonst seine Background-Farbe nicht.

Über eine weitere Schleife wird das TImage-Array "meteor_imga" gefüllt. Dazu wird pro Meteor ein TImage erzeugt, mit dem TPicture aus TImage "meteorimg" versehen und auf dem TPanel "meteorcp" abgelegt. Dort sind später alle noch im Spiel vorhandenen Meteore aufgelistet. Wird ein Meteor abgeschossen, so verschwindet sein zugehöriges Bild einfach vom TPanel.

Jetzt wird die OpenGL-Umgebung initialisiert. Kommt es dabei zu Problemen, bricht das Programm ab. Als Ziel der Grafikausgabe wird das TPanel "viewp" definiert.

Es folgt die Routine zum Einlesen der Programm-Parameter aus dem Konfigurationsfile "ogl_iss.ini". Hier wird u.a. festgehalten, welcher Grafik-Modus aktiv ist, ob Sound zu hören ist oder nicht, oder ob das Cockpit angezeigt werden soll. Des Weiteren sind hier die Highscores der vier Spiel-Level "rookie", "advanced", "profi" und "mad" abgelegt.

Danach wird die Prozedur "initobjects" aufgerufen, die wir uns gleich näher ansehen werden.

Mittels "self.WindowState:=wsmaximized" wird das Programm-Fenster maximiert. Das hat einige weitere Designarbeiten zur Folge. Ausserdem wird dabei die OpenGL-Umgebung auf die neuen Bildausgabe-Verhältnisse angepasst:

Anschliessend wird der TTimer "frequencyt" aktiviert, wodurch die sich periodisch wiederholende Grafikausgabe begonnen wird.

Und zuletzt wird dann noch die Prozedur "game_start_show" aufgerufen.

3.3.4. Form-Zerstörung

Das Gegenstück zu "FormCreate" ist "FormDestroy", welches beim Beenden des Programms ebenfalls automatisch aufgerufen wird. Hier werden alle Ressourcen wieder freigegeben und einige Programm-Parameter sowie die (aktualisierten) Highscore-Listen in die Konfigurationsdatei geschrieben:

3.4. Objekte und Texturen initialisieren

3.4.1. Objekte

Wie wir gesehen haben, wird in "FormCreate" die Prozedur "initobjects" aufgerufen:

Hier werden "gluQuadric"-Objekte erzeugt. Solche Objekte lassen sich mit bestimmten Eigenschaften versehen und später an diverse OpenGL-Funktionen übergeben.

3.4.1.1. Weltallkugel

Das "gluQuadric"-Objekt "space_quad" wird zum Beispiel später als Kugel dargestellt, an deren Mittelpunkt sich die ISS befindet. Sie ist so gross, dass sie als Art "Himmelszelt" fungiert. Egal, in welche Richtung wir später auch schauen, wir sehen stets die Innenwände dieser Kugel im Hintergrund. Über die Funktion "img2tx" wird eine passende Textur an das Objekt gebunden. Wie das genau funktioniert, sehen wir uns gleich an.

Textur von 'space_quad': Ein 256 x 128 Pixel grosses JPG-Bild für den Weltraum.

Einsatz der Space-Textur: Der Weltraum um uns herum ist nicht einfach schwarz, sondern von blau leuchtenden Nebelbändern durchzogen.

3.4.1.2. Erdkugel

Ähnlich wie "space_quad" ist auch "earth_quad" konzipiert. Hierbei handelt es sich um den "Zeiger" auf die Erdkugel, die 345 km unter der ISS um ihre eigene Achse rotiert. Sie hilft uns bei der Orientierung im Raum, wenn wir später um die ISS herumfliegen. Obgleich natürlich solche Dinge wie oben und unten im schwerelosen Zustand nicht wirklich eine Rolle spielen.

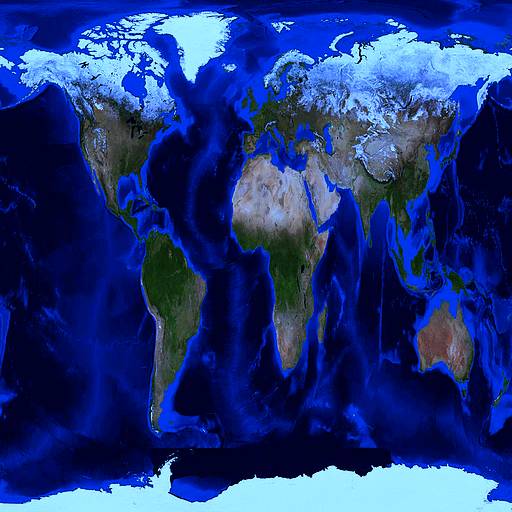
Textur von 'earth_quad': Ein geometrisch angepasste Grafik mit den Kontinenten und Ozeanen, 512 x 512 Pixel gross - und damit die mit Abstand grösste verwendete Textur.

Einsatz der Earth-Texture: Die blaue Heimat, rotierend unter der ISS, mit seinen einigermassen korrekt wiedergegebenen Strukturen.

3.4.1.3. ISS

Die ISS selbst verfügt über das "gluQuad"-Objekt "iss_quad". Dieses wird später beim Rendern mehrfach verwendet, für jedes Einzelteil der ISS erneut. Ausmasse und Texturen werden dabei jeweils zuvor angepasst. Die verwendeten Texturen sind:

Textur 'iss_big_tx': Grafik für den Hauptkörper der ISS.	Textur 'iss_big_sail_tx': Grafik für die grossen Segel der ISS.
Textur 'iss_small_tx': Grafik für die kleinen Gondeln der ISS.	Textur 'iss_small_sail_tx': Grafik für die kleinen Gondeln der ISS.

Einsatz der ISS-Texturen: Die ISS von Aussen und Innen. Nur vier Texturen genügen, um unserer Raumstation ein hinreichend realistisches Aussehen zu verleihen.

Zusätzlich wird der Positionsvektor der ISS definiert. Sie wird so platziert, dass ihr Zentrum genau auf dem Ursprung (0,0,0) liegt.

3.4.1.4. Meteore

Zuletzt werden dann noch die Meteore mit zwei Texturen versehen:

Textur 'meteor_tx': Grafik für die Meteore, die die ISS umschwirren.

Textur 'meteor_explode_tx': Grafik für explodierende Meteore.

Einsatz der Meteor-Texturen: Meteore steuern auf die ISS zu - und explodieren bisweilen ...

3.4.2. Texturen

3.4.2.1. Bilder über spezielle OpenGL-DLLs

Bei den Quellcodes zu OpenGL, die man im Web so findet, werden Texturen üblicherweise nach dem Programmstart von der Festplatte nachgeladen. Die Units "sdl" und "sdl_image" bieten dafür auch in Delphi die nötige Funktionalität.

Die Methode hat jedoch den Nachteil, dass für die Installation neben dem Programm stets alle Bilder extra mitgeliefert werden müssen (und unter Umständen auch die Bibliotheksdateien "sdl.dll" und "sdl_image.dll").

3.4.2.2. Bilder ohne DLLs und Plattenzugriffe

Bei "OGL_ISS" ist das nicht nötig, denn hier können die Texturen direkt aus TImage-Bildern generiert werden. Das Ganze wurde dabei von mir so gelöst, das die Bibliotheksdateien "SDL"- und "SDL_image.dll" ebenfalls nicht vorhanden sein müssen.

Betrachten wir zunächst die Funktion "img2tx":

An die Funktion wird das TImage-Objekt "img" übergeben, welches ein beliebiges, vorgeladenes Bild enthält. Es kann sich dabei ebenso um ein GIF, wie ein JPG, eine Bitmap oder irgendein anderes Bildformat handeln. Denn im ersten Schritt wird das enthaltene TPicture sowieso in eine Bitmap "bmp" mit 32 bit Farbtiefe umgewandelt.

Anschliessend wird das LongWord-Array "data" erzeugt, welches gross genug ist, um alle anfallenden Bilddaten komplett aufnehmen zu können.

Das Bild wird nun pixelweise durchlaufen, der Farbwert jedes Pixels auf geheimnisvolle Art umgerechnet - den Teil habe ich mir im Web geklaut - und in das "data"-Array eingetragen.

Das "data"-Array wird daraufhin an die Funktion "createTexture" übergeben, welche letztlich einen von OpenGL verwendbaren "Textur-Index-Wert" zurück liefert:

3.5. Programm-Taktung: Timer-gesteuerte Action

3.5.1. Computer sind verschieden

Als ich begann, "OGL_ISS" mit einem kleinen Spiel zu versehen, wurde schnell klar, dass man nur dann spielbare Ergebnisse erzielen würde, wenn das Ablauftempo des Ganzen halbwegs "normiert" wird. Computer sind nämlich bekanntlich verschieden schnell - und einige besitzen 3D-Grafikkarten, andere nicht. Bedingt dadurch wird die Geschwindigkeit, mit der OpenGL die Objekte rendern und letztlich zur Anzeige bringen kann, für den Programmierer schwer abzuschätzen.

3.5.2. Timer- statt OnIdle-Ereignisse

Aus diesem Grund wird die Grafikverarbeitung in "OGL_ISS" nicht über das OnIdle-Ereignis der Applikation gelöst, wie sonst meist üblich, weil es die beste Performanz bringt. Stattdessen gibt es einen TTimer "frequencyt", der diesen Job in regelmässigen, definierten Zeitabständen erledigt.

Wann immer dieser TTimer "feuert" - und dies geschieht alle paar Millisekunden, je nach Einstellung der TTrackBar "frequencytb" -, wird die folgende Prozedur ausgeführt:

3.5.2.1. Zähler-Update

Am Anfang werden die Rotationszähler "frequ_fast", "frequ_low" und "earth_rot" auf verschieden starke Weise erhöht. Sie dienen dazu, periodisch einige Elemente der ISS zu bewegen, etwa die grossen Solar-Segel, oder die Erde genau so schnell rotieren zu lassen, dass in 90 Minuten eine komplette Rotation erfolgt (so viel bzw. wenig Zeit benötigt nämlich auch die echte ISS für die Erdumrundung).

3.5.2.2. User-Eingaben-Check

Anschliessend wird geprüft, ob der Anwender eine der Flugsteuerungstasten betätigt hat. Ist dies der Fall, werden sie entsprechend abgearbeitet. Wurde zusätzlich die "STRG"-Taste ("actrl") gedrückt, dann gilt:

• Cursor hoch/runter: Rotation um x-Achse (Rotations-Delta: "rx_speed")
• Cursor recht/links: Rotation um z-Achse (Rotations-Delta: "rz_speed")

Ansonsten gilt:

• Cursor hoch/runter: Flug geradeaus nach vorne/hinten (Positions-Delta: "pspeed" und "dposv")
• Cursor recht/links: Rotation um y-Achse (Rotations-Delta: "ry_speed")

3.5.2.3. Kalkulation von Rotations- und Positions-Delta

Über die internen Funktionen "rotate_axis" und "flight" wird dazu jeweils das zugehörige Rotations- bzw. Positionsdelta berechnet (siehe obige Liste).

Das Rotationsdelta wird einfach um einen konstanten Wert erhöht oder gemindert. Wird dabei der Rotationswinkel von 360 Grad überschritten, beginnt es wieder bei 0 Grad. Die Stärke der Änderung wird auf "_rspeed_max" begrenzt, damit wir am Ende nicht völlig orientierungslos und in in rasender Geschwindigkeit durch den Raum rotieren.

Das Positionsdelta ist komplizierter zu berechnen. Dafür müssen wir nämlich feststellen, in welche Richtung aktuell geschaut wird, damit wir exakt geradeaus steuern können. Hier kommen die Rotationsmatrizen zum Einsatz, die wir in "DanGeoU.pas" definiert haben. Dem Thema widmen wir uns weiter unten im Kapitel "Fliegen im dreidimensionalem Raum".

Je länger eine Steuerungstaste betätigt wird, desto grösser wird das Rotations- bzw. Positionsdelta pro Timer-Aufruf; man beschleunigt also. Wird die Taste wieder losgelassen, sorgt die interne Prozeduren "slowspeed" dafür, dass die verschiedenen Delta-Variablen langsam wieder auf null zurückgehen; man bremst also ab.

Ist der automatische Heimflug aktiviert ("flyhome_c" ist grösser Null), dann werden übrigens alle Steuerungseingaben ignoriert. Der Pilot muss in diesem Fall warten, bis der Ursprungsort erreicht ist, bevor er wieder selbst aktiv werden kann.

3.5.2.4. Cockpit-Update

Nachdem unsere Position und Geschwindigkeit im Raum neu gesetzt wurde, wird weiter geprüft, ob das Cockpit sichtbar ist. Ist dem so, dann werden jetzt diverse Statusmeldungen auf dem Bildschirm ausgegeben.

Cockpit: Das Cockpit unseres Raumschiffs mit den Status-Informationen (oben). Es lässt sich auch jederzeit optional abschalten, was den Sichtbereich vergrössert (unten).

Anschliessend wird über die Prozedur "draw_scene" die aktuelle Grafikausgabe initiiert.

Zuletzt wird dann noch einmal geprüft, ob wir uns im automatischen Heimflug befinden, und ob wir das Ziel bereits erreicht haben. Wenn ja, werden alle Deltas auf null gesetzt - unser Raumschiff steht still. Weiterhin wird geklärt, ob der automatische Heimflug freiwillig geschah oder erzwungen wurde, weil die ISS von einem Meteor getroffen worden ist. In letzterem Fall wird eine schöne, grosse, finale Explosion vorbereitet :-)

3.6. Fliegen im dreidimensionalem Raum

Die Programmierung von "OGL_ISS" lief eigentlich wie am Schnürchen. Die einzige Geschichte, bei der ich wirklich zu kämpfen hatte, war der vermeintlich einfache Flug geradeaus.

Bei "OGL_Henrys" und "OGL_Planets" wurde bereits eine Steuerung zum Navigieren durch einen 3-dimensionalen Raum realisiert. Dort konnte man jedoch nur senkrecht zu der y-Achse nach oben und unten fliegen, nicht jedoch in "schräger" Weise gleichzeitig nach vorne und nach unten.

3.6.1. Probleme mit der Fadenkreuz-Navigation

Einfacher gesagt: Was ich diesmal wollte, war eine Steuerung, die das Raumschiff immer exakt in Richtung des im Fadenkreuz ausgewiesene Zieles fliegen liess, egal, wie sehr die Raum-Achsen auch verstellt waren.

Ich malte also viele kleine Bildchen, kombinierte Sinus- und Kosinus-Werte, spielte mit dem Vorzeichen herum und versuchte mich am Ende sogar an der Verwendung der Tangens-Funktion.

Mathematische Gehversuche: Die blöde Rotation zur zielgenauen Navigation im dreidimensionalen Raum muss doch irgendwie in dem Griff zu bekommen sein ...

Nach drei Tagen (!) gab ich auf. Musste in Mathematik Nachsitzen. Las Vektoren- und Matrizen-Tutorials. Baute dabei die "DanGeoU.pas" zusammen. Und knackte so schliesslich das Problem mit etwas Web-Hilfe.

3.6.2. Positionsänderung

Schauen wir uns noch einmal den - etwas vereinfachten - Code zur Modifikation des Positionsdeltas aus der "frequencytTimer"-Prozedur an:

Das eigentliche Positionsdelta "pspeed" wird ähnlich wie die Rotationsdeltas einfach nur um einen konstanten Wert erhöht oder gemindert. Damit wissen wir schon einmal, wie stark unsere Position im Raum geändert werden soll.

3.6.3. Richtungsänderung

Damit ist aber noch nicht geklärt, in welcher Richtung sich die Änderung auswirken soll. Für diesen Job muss der aktuelle Richtungsvektor "dposv" bestimmt werden.

Sind alle Achsen-Winkel auf null, dann ist die Richtung klar: Da wir als Piloten in den Raum hineinschauen, müssen wir uns nur entlang der z-Achse ins Negative bewegen, um nach vorne zu fliegen. Der Richtungsvektor ist in diesem Fall einfach v=(0,0,-1). Die x- und y-Positionen bleiben völlig unverändert.

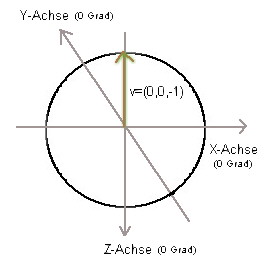
Richtungsvektor vor der Rotation: Der ursprüngliche Richtungsvektor 'v' zeigt exakt nach vorne, in die gewünschte Richtung.

Rotieren wir nun aber 45 Grad um die y-Achse (positive Rotationen erfolgen übrigens immer entgegen dem Uhrzeigersinn - auch so eine Sache, die ich Stoffel erst nach einer ganzen Weile merkte), dann bedeutet ein Flug entlang der z-Achse, dass wir nicht mehr geradeaus fliegen, sondern schräg nach links hinten. Um die korrekte Richtung einzuhalten, muss in diesem Fall nämlich auch die x-Position geändert werden.

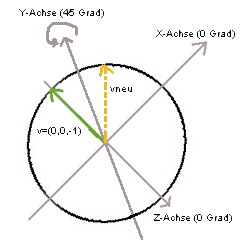
Richtungsvektor nach der Rotation: Der Richtungsvektor 'v' wurde um 45 Grad um die y-Achse rotiert. Nun zeigt er nach schräg nach links hinten. Tatsächlich wollen wir uns aber in die neue Richtung 'vneu' bewegen. Wie finden wir diesen Vektor?

Noch komplizierter wird es natürlich, wenn zudem um die x-Achse rotiert wird. Spätestens jetzt gilt es, alle Koordinaten-Werte, also x, y und z, durch den Richtungsvektor "dposv" anzupassen, um in die vom Fadenkreuz vorgegebene Richtung zu fliegen.

Und wie erhalten wir nun den gesuchten Richtungsvektor "vneu" (="dposv")?

Indem wir den ursprünglichen Richtungsvektor, nämlich v=(0,0,-1), alle vorgegebenen Achsen-Rotationen nachmachen lassen. Denn dann sollte dieser wieder genau in die Richtung weisen, in die wir selbst gerade schauen.

Der Source-Code dazu ist:

3.6.4. Hilfe durch Rotations-Matrizen

Wir bilden uns zuerst die generalisierte Rotationsmatrix, indem wir die drei Achsen-Rotationsmatrizen bestimmen und diese dann miteinander multiplizieren. Wie in "DanGeoU.pas" beschrieben, "merkt" sich die so entstandene Matrix "m" alle Rotationen ihrer Teiler-Matrizen "mx", "my" und "mz".

Jetzt muss man nur noch den ursprünglichen Richtungsvektor mit der generalisierten Rotationsmatrix "m" multiplizieren. Als Ergebnis erhält man den denjenigen Vektor, der in unserem Modell exakt nach vorne weist. Multipliziert mit dem Positionsdelta "pspeed" und aufaddiert zum Positionsvektor "posv" erhalten wir schliesslich die neue Position im Raum.

Eigentlich doch ganz einfach ...

3.7. Spiel-Auswahl

3.7.1. Die Qual der Wahl

Bevor der TTimer "frequencyt" in "FormCreate" aktiviert wird, wird "game_start_show" aufgerufen (siehe weiter oben).

3.7.1.1. Level-Auswahl

Hier werden einige Programm-Parameter zurückgesetzt und das TPanel "gamestartp" sichtbar gemacht. Über die Tastatur kann dann u.a. der gewünschte Spiel-Level ausgewählt werden.

Spielstart-Fenster: Erklärung der Tastaturkürzel und die Auswahl verschiedener Programm-Optionen.

3.7.1.2. Taktfrequenz-Auswahl

Mittels der TTrackBar "frequencytb" lässt sich einstellen, mit welcher Taktfrequenz die "frequencytTimer"-Prozedur aufgerufen wird (und damit auch "draw_scene"). Das Intervall reicht von einer bis bis 100 Millisekunden. Je nach Rechnergeschwindigkeit kann der Anwender hier einen für sich passenden Wert einstellen.

3.7.2. Wenn der User drückt - Tastatur-Ereignisse abfangen

Alle Tastatur-Eingaben des Benutzers werden über die Prozeduren "FormKeyDown" und "FormKeyp" verwaltet.

Zunächst wird geprüft, ob der automatische Heimflug aktiviert ist. In diesem Fall werden alle Benutzer-Eingaben ignoriert.

Der Status der "Strg"-Taste wird in der Variablen "actrl" gesichert. Sollte eine der Flugsteuerungstasten betätigt worden sein, so wird "akey" gesetzt und die Prozedur verlassen. Wie wir gesehen haben, erfolgt deren Abarbeitung in der Prozedur "frequencytTimer".

Wird das TPanel "gameoverp" mit der aktuellen Highscore-Liste angezeigt, befinden wir uns am Spiel-Ende. In diesem Fall wird nur auf die "Return"-Taste reagiert.

Befinden wir uns am Spiel-Start, dann ist das TPanel "gamestartp" sichtbar. Jetzt reagieren wir insbesondere auf die Tasten "1" bis "5", mit denen sich der Spiel-Level auswählen lässt. Dazu wird in der Folge die Prozedur "game_start" aufgerufen.

Sind übrigens die TPanels "gamestartp" und "gameoverp" nicht sichtbar, dann befinden wir uns im laufenden Spiel.

Die "G"-Taste wechselt durch Erhöhung des "graphic_mode"-Zählers den Grafik-Modus, mit dem in "draw_scene" das Modell gerendert wird.

Die Tasten "C", "P", "S" und "V" aktivieren bzw. deaktivieren die Anzeige des Cockpits, die Sichtbarkeit des Flug-Pfades, die Sound-Effekte und das Visier mit dem Fadenkreuz.

Mittels "F"-Taste wird der automatische Heimflug in Gang gesetzt.

Über "Space" werden Schüsse abgegeben.

Und "Escape" bricht letztlich das laufende Spiel ab oder beendet das Programm.

3.8. Spiel-Start

3.8.1. Programm-Parameter setzen

Haben wir ein Spiel-Level ausgewählt, wird die Prozedur "game_start" aufgerufen:

Der Benutzer wird an die Startposition im Spiel transportiert, indem die Achsen-Rotation auf null gesetzt und der Positions-Vektor "posv" auf 200 m ("_pos_home_z") vor der ISS initialisiert wird.

Je nach Spiel-Level wird nun die Anzahl der Meteore "game_meteor_c" differiert, die auf die ISS zufliegen werden. Ihre maximale Entfernung von der ISS zu Beginn des Spieles steht in "game_meteor_dim". Und über "game_meteor_speed" wird eingestellt, wie schnell die Meteore später fliegen dürfen.

Es gilt: Je höher der Spiel-Level, desto grösser die Anzahl der Meteore, desto kleiner die Entfernung von der ISS, und desto schneller die Meteore. Während es beim Spiel-Level "_game_level_train" gar keine Meteore gibt, sind es bei "_game_level_mad" deren sehr viele, sehr schnelle und sehr nahe :-)

Alle im Spiel aktiven Meteore werden anschliessend auf dem TPanel "meteorcp" sichtbar gemacht, anschliessend die Start-Bedingungen über die Prozedur "meteor_set" gesetzt.

Indem das TPanel "gamestartp" unsichtbar gemacht wird, wechseln wir automatisch in in den aktiven Spiel-Modus.

3.8.2. Meteore verteilen

Der Spiel-Level gibt vor, wie viel Meteore im Spiel vorkommen und abgeschossen werden müssen. Auch ihre Verteilung im Raum und ihre Geschwindigkeit hängt davon ab. Die nötigen Einstellungen nimmt die Prozedur "meteor_set" für jeden einzelnen Meteor extra vor:

Zuerst wird per Zufall eine Position des Meteors gesetzt. Danach wird geprüft, ob die Distanz des Meteors zur ISS dem Spiel-Parameter "game_meteor_dim/2" genügt (das wird über die "DanGeoU"-Funktion "v_distance" berechnet). Ist der Meteor zu nahe, dann wird eine neue, zufällige Position vergeben.

Anschliessend erhält der Meteor einen zufallsbedingt grossen Radius, wird auf den Status "_meteor_state_fly" gesetzt, und bekommt eine bestimmte Flug-Geschwindigkeit verpasst.

3.9. Spiel-Ablauf

3.9.1. Szenen-Rendering

Das TPanel "gamestartp" ist unsichtbar, der TTImer "frequencyt" ist aktiviert, die Spiel-Parameter alle gesetzt, alle Meteore initialisiert - das Spiel hat begonnen.

Wie oben gezeigt, wird durch die Prozedur "frequencytTimer" in regelmässigen Abständen die zentrale Prozedur "draw_scene" aufgerufen, die wir uns jetzt näher anschauen wollen.

Zu Beginn wird anhand des Parameters "graphic_mode" bestimmt, welche Elemente der Szenerie gemalt werden sollen und welche nicht. Zudem wird eingestellt, ob Texturen Verwendung finden oder stattdessen nur ein Gittermodell angezeigt wird.

3.9.1.1. Acht Grafik-Modi

Insgesamt gibt es acht verschiedene Grafik-Modi, die die Ausgabe über die booleschen Variablen "graphic_txok", "graphic_earthok" und "graphic_spaceok" regulieren. Es gilt:

Grafik-Modus graphic_mode	Texturen graphic_txok	Erde graphic_earthok	Weltall space_txok	Beispiel
0	Nein	Nein	Nein
1	Nein	Nein	Ja
2	Nein	Ja	Nein
3	Nein	Ja	Ja
4	Ja	Nein	Nein
5	Ja	Nein	Ja
6	Ja	Ja	Nein
7	Ja	Ja	Ja

Nachdem der Grafik-Modus bestimmt ist, wird mit "glClear" der OpenGL-Speicher gelöscht und mit "glLoadIdentity" zum Ursprungsort transportiert.

3.9.1.2. Wo sind wir im Modell?

Es folgt die Ausrichtung des Modells gemässt des Rotation-Vektors "rotv" sowie unsere Positionierung im Raum gemäss des Position-Vektors "posv".

Je nach Grafik-Modus wird dann das Weltall und/oder die Erde gezeichnet. Diese "draw_"-Routinen sehen wir uns gleich näher an.

Danach wird geprüft, ob die ISS noch vorhanden oder bereits durch einen Meteor zerstört wurde. Gemalt wird sie natürlich nur, wenn sie noch existiert.

Anschliessend werden die Meteore gezeichnet, sofern wir uns nicht gerade im Spiel-Level "_game_level_train" befinden. Die Schüsse, die wir abgegeben haben, werden nur so lange angezeigt, wie die ISS nicht von einem Meteor getroffen wurde.

Der boolesche Parameter "draw_path_ok" gibt vor, ob unsere bisherige Flugroute im Modell optisch gekennzeichnet werden soll.

Ein weiterer boolescher Parameter, "draw_visor_ok", reguliert, ob das Visier vorhanden ist oder nicht.

Mittels der OpenGL-Prozedur "SwapBuffers" wird das Modell letztlich auf dem TPanel "viewp" zur Anzeige gebracht.

3.9.1.3. Der Welten-Raum wird gemalt

Um den Hintergrund etwas interessanter zu gestalten, wird um unserer Position herum eine gewaltige Kugel gezeichnet, innerhalb der wir uns bewegen. Wir können diese Kugel praktisch nicht verlassen und sehen daher stets auf ihre Innenwände.

Die Kugel wird mittels der OpenGL-Prozedur "gluSphere" realisiert. Ihr Mittelpunkt ist im Ursprung, ihr Radius "_space_r" doppelt so gross wie der Erdradius ("_earth_r", das sind 6368000 m).

Zuvor wird über die Prozedur "graphic_bind_mode" bestimmt, ob die Kugel mit Texturen versehen oder als Gittermodell gezeichnet werden soll.

Falls der Grafik-Modus ein reines Gittermodell vorsieht, bleiben die Texturen deaktiviert. Stattdessen wird jedoch die Farbe angepasst, mit der die Gitterlinien gezeichnet werden sollen.

Die Prozedur "graphic_mode_off" schaltet Texturen generell ab, egal, ob sie zuvor aktiviert wurden oder nicht.

Prozedur 'draw_space': Der Hintergrund wird gemalt. Eine riesige Sphäre um den Ursprung. it einer dunklen Textur, die das Weltall wiedergibt.

3.9.1.4. Die Erde wird gemalt - Home, sweet home

Auch die Erde wird mittels "gluSphere" gezeichnet. Ihr Mittelpunkt befindet sich zu Beginn des Spiels 345 km (Höhe ISS) plus 6368 km (Erd-Radius) unter dem Ursprung.

Anders als die Weltall-Kugel sehen wir die Erde von aussen. Daraus resultierten - Grrr! - wieder einmal Probleme mit dem Tiefenpuffer, denn die Erd-Kugel erschient stellenweise transparent, sodass man durch sie hindurch ihre "Rückwand" sehen konnte.

Wiedergabefehler bei der Prozedur 'draw_earth': Aufgrund ihrer immensen Grösse erscheint die Erdkugel zur Hälfte transparent, weil der Tiefenpuffer-Bereich überschritten wird. Dies muss verhindert werden. Doch wie?

Aus diesem Grund wird die Erde um den Faktor "_scale" (=100) verkleinert, ebenso ihr Abstand zur ISS. Damit kam der Tiefenpuffer glücklicherweise zurecht.

Jetzt bestand jedoch die "Gefahr", dass man in die Erd-Kugel eintauchte, wenn ein paar Minuten senkrecht nach unten geflogen wurde. Um dies zu verhindern, wandert der Mittelpunkt der Sphäre parallel zu unserer Raum-Position mit, sodass stets ein konstanter Abstand eingehalten wird. Egal, wie lange wir auch fliegen, wir erreichen den Erdboden nie.

Bisschen billig, die Lösung, aber sie funzt.

3.9.1.5. Die ISS wird zusammengebaut

Die ISS ist komplizierter aufgebaut als Weltall und Erde. Sie setzt sich aus mehreren, sich teilweise wiederholenden, Elementen zusammen. Die ASCII-Grafiken über dem Funktions-Rumpf deuten an, wo wann was wie gross gemalt wird.

Die Konstruktion im 3-dimensionalen Raum ist relativ schwierig, weil nach jeder Rotation die Winkel in eine andere Richtung weisen, als man vielleicht vermuten würde.

Statt z.B. ein Element der ISS, etwa ein Solar-Segel, durch Verringerung des "z"-Wertes weiter nach hinten zu platzieren, passiert es dann, dass es nach einer Rotation von 90 Grad um die y-Achse weiter links landet. Tatsächlich müsste jetzt nämlich der "x"-Wert erhöht werden, um den gewünschten Effekt zu erreichen.

Aus diesem Grund habe ich in der Konstruktionsphase einen zusätzliche Positions- und einen zusätzlichen Rotations-Vektor verwaltet. Diese liessen sich über bestimmte Tastatur-Eingaben verändern. Vor der Platzierung eines ISS-Elements liess ich das Modell dann gemäss dieser Vektoren rotieren und transportieren. So war leicht zu erkennen, welcher Wert optisch was bewirkt.

Die Erläuterung, wie die ISS nun genau konstruiert wird, ist müssig und erspare ich uns hier.

Prozedur 'draw_iss': Wiedergabe der internationale Raumstation ISS in unserem OpenGL-Raum. Hier sieht man sie schräg von unten. Was man nicht sieht: Die grossen und kleinen Segel rotieren in periodischen Abständen stufenweise um den Rumpf.

3.9.2. Meteor-Handling

3.9.2.1. Platzierung der Killer-Meteore

Nach der ISS werden in "draw_scene" die Meteore gezeichnet - auf ihrem zerstörerischen Weg direkt zur Raumstation ...

Die maximale Anzahl aktiver Meteore wird Level-abhängig von "game_meteor_c" vorgegeben. In einer Schleife werden alle Meteore des "meteor_a"-Arrays einzeln abgerufen und über den Pointer "pm" angesprochen.

Meteore kennen drei Status ("pm.state"):

1. "_meteor_state_none": Der Meteor ist inaktiv/zerstört
2. "_meteor_state_fly": Der Meteor ist unterwegs zur ISS
3. "_meteor_state_explode": Der Meteor ist gerade am explodieren

Hat der aktuell betrachtete Meteor den Status "_meteor_state_non", dann ist er inaktiv und wird nicht weiter beachtet.

Hat ein Meteor den Status "_meteor_state_explode", dann fliegt er gerade auseinander. Die Dauer der Explosion hängt vom Meteor-eigenem Zähler "pm.count" ab. Dieser wird zu Beginn auf einen bestimmten Wert hochgesetzt und innerhalb jeder Zeiteinheit um eins dekrementiert. Steht der Zähler schliesslich auf null, hat der Meteor ausgedient und verpufft ins Nichts.

Im Explosionsfall wird zusätzlich geprüft, ob die Zerstörung des Meteors durch einen Anwender-Schuss verursacht wurde oder durch Kollision mit seinem Ziel, der ISS.

Bei Explosion durch ISS-Kontakt endet das Spiel an dieser Stelle; es wird dann nur noch die Prozedur "game_over_show" aufgerufen.

Hat dagegen der Anwender den Meteor erfolgreich zerstört, bekommt er Punkte auf seinem Konto gutgeschrieben. Dabei gilt, dass er umso mehr Punkte bekommt, je weiter der Meteor von der ISS entfernt war.

Ist der Meteor dagegen noch fröhlich unterwegs, wird über die interne Prozedur "gozero" seine Position neu berechnet. Diese wird so kalkuliert, dass der Meteor sich der ISS unweigerlich nähert.

Falls der Meteor noch völlig intakt sein sollte ("pm.state ungleich _meteor_state_explode"), wird sein aktueller Abstand zur ISS berechnet. Die dabei gefundene geringste Distanz aller Meteore wird in "dissmin" gemerkt.

Weiterhin bleibt zu prüfen, ob der Meteor von einem Anwender-Schuss getroffen wurde. Dazu werden in einer Schleife alle Schüsse des "shot_a"-Arrays durchgegangen.

Steht der Zähler "ps.count" des aktuell betrachteten Schusses auf null, befindet er sich noch im Magazin und wird daher ignoriert.

Ansonsten wird seine aktuelle Position ("ps.posv") und seine vorherige Position "ps.poslastv" als Anfang und Ende einer Linie interpretiert. Die Funktion "LineInSphere" testet anschliessend, ob diese Linie an irgendeiner Stelle die Meteor-Kugel berührt.

Ist dies der Fall, wurde der Meteor getroffen. Er wechselt auf den Status "_state_meteor_explode" und bekommt seinen Explosions-Zähler "pm.count" hochgesetzt.

Es folgt die Ausgabe des Meteors über die interne Prozedur "draw_meteor". Je nach Status wird eine passende Textur vergeben und im Explosionsfall zusätzlich der Radius vergrössert sowie der Explosions-Zähler dekrementiert.

Prozedur 'draw_meteors': Alle Meteore werden über nur eine Prozedur im OpenGL-Raum wiedergegeben. Hier hat einer dieser Gesteinsbrocken gerade die ISS erwischt - und explodiert nun als hell erleuchtete Feuerkugel.

Schliesslich wird noch der Abstand zu unserem Raumschiff berechnet. Die so gefundene geringste Distanz aller Meteore wird in "dmemin" gesichert und später im TPanel ""detect_mep" ausgegeben:

Meteor-Detektor Raumschiff (ME): Die MD-ME-Anzeige zeigt an, wie weit der nächste Meteor von unserem Raumschiff entfernt ist. Man kann diese Anzeige daher nutzen, um die Meteore in den Weiten des Alls aufzuspüren. So kann man sie gezielt vernichten, bevor sie die ISS erreichen.

Nachdem schliesslich alle Meteore abgearbeitet wurden, bleibt nur noch zu prüfen, ob der der ISS nächste Meteor den kritischen Wert von "_meteor_alarm" Metern unterschritten hat. Ist dem so, wird ein Alarmsignal initiiert.

Meteor-Detektor ISS: Die MD-ISS-Anzeige zeigt an, wie weit weg sich der nächste Meteor von der ISS befindet. Hier ist einer dieser Gesteinsbrocken gerade innerhalb des kritischen Bereichs um die ISS geflogen - und der Detektor heult sofort los.

3.9.2.2. Ballerei - Linie trifft Sphäre

Den folgenden Source habe ich im Web gefunden und nur etwas für meine Zwecke adaptiert.

Die in C++ geschriebene Funktion hiess ursprünglich "LineHitsSphere" und lieferte nur dann "true" zurück, wenn die Linie die Kugel komplett durchquerte.

Mir genügt es, wenn auch nur Teile der Linie irgendwo im Inneren der Kugel auftauchen. Daher heisst das Teil bei mir auch "LineInSphere":

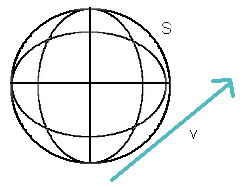
Funktion 'LineInSphere' - Fall 1: Der Vektor 'v' berührt die Sphäre 'S' an keiner Stelle. 'LineInSphere' liefert 'false' zurück.

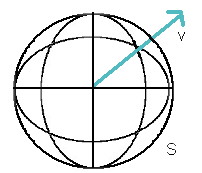
Funktion 'LineInSphere' - Fall 2: Der Vektor 'v' beginnt im Inneren der Sphäre 'S', durchkreuzt sie also nicht vollständig. 'LineInSphere' liefert in diesem Fall nur dann 'true' zurück, wenn 'crossok' inaktiv ist.

Funktion 'LineInSphere' - Fall 3: Der Vektor 'v' durchquert die Sphäre 'S' vollständig. 'LineInSphere' liefert unabhängig von 'crossok' stets 'true' zurück.

Ich habe mir nicht die Mühe gemacht, den Source völlig zu verstehen. Daher gibt es hier auch keine weitere Erklärung dazu.

3.9.2.3. Schuss-Salven

Wie wir im Kapitel "Wenn der User drückt" gesehen haben, bewirkt die "Space"-Taste, dass die Prozedur "shot" aufgerufen wird. Hier werden die Start-Parameter der Schüsse berechnet, die in "draw_scene" mittels Prozedur "draw_shots" ausgegeben werden.

Betrachten wir zunächst "shots":

Ähnlich wie beim Geradeausflug wollen wir, dass die Geschosse exakt in diejenige Richtung fliegen, die unser Blick in den Raum hinein vorgibt.

Dazu holen wir uns den aktuellen Richtungsvektor - also den ursprünglichen Richtungsvektor (0,0,-1) rotiert um alle Achsen - über die bereits beschriebene Funktion "getlookv".

Jetzt wird das Schuss-Array "shot_a" durchlaufen und nach insgesamt "_max" (=10) freien Geschossen durchsucht. Finden wir keine, können wir nichts abfeuern und müssen warten, bis die letzten, noch aktiven Schüsse abgeklungen sind.

Haben wir ein freies Geschoss "ps" gefunden, so erhält es unsere aktuelle Position ("ps.posv") und die berechnete Richtung ("ps.dirv"). Der Zähler "ps.count" wird hochgesetzt und gibt an, wie viele Zeiteinheiten der Schuss unterwegs sein wird.

Der erste Schuss fliegt exakt in die Mitte, die weiteren Schüsse werden so berechnet, dass sie sich kreisförmig um das Zentrum anordnen. Dazu nutzen wir die Formeln für die Vektor-Rotation um x- und y-Achse.

Am Schluss werden dem Spieler noch Punkte abgezogen. Man sollte also nicht zu wahllos herumschiessen, wenn man ernsthaft einen neuen Highscore anvisiert.

Und nun die Ausgabe der Geschosse durch die Prozedur "draw_shots":

Das Schuss-Array "shot_a" wird durchlaufen und nach aktiven Geschossen ("count ungleich 0") durchsucht. Werden keine gefunden, gibt es nichts weiter zu tun und wir verlassen die Prozedur wieder.

Aktive Geschosse erhalten den Pointer "ps". Wir sichern die aktuelle Position des Schusses in "ps.poslastv". Die neue Position ergibt sich durch Vektor-Addition der aktuellen Position mit dem Richtungsvektor, der in der Prozedur "shots" in "ps.dirv" eingetragen wurde.

Die letzte Position und die neue aktuelle Position des Schusses beschreiben eine virtuelle Linie, die das Geschoss innerhalb der letzten Zeiteinheit durchflogen hat. Diese Linie wird verwendet, um festzustellen, ob ein Meteor getroffen wurde (siehe Kapitel "Angriff der Killer-Meteore" und "Linie trifft Sphäre").

Mittels "v_scale", angewendet auf "ps.dirv", sorgen wir weiterhin dafür, dass das Geschoss zunehmend schneller wird.

Der Zähler "ps.count" wird dekrementiert. Hat er Null erreicht, wissen wir später, dass das Geschoss verpufft ist. Es steht dann für den nächsten Schuss wieder frei zur Verfügung.

Zuletzt wird der Schuss-Salve dann über die OpenGL-Prozedur "gluSphere" in den Grafikpuffer gemalt.

Prozedur 'draw_shots': Wiedergabe der Schüsse, die von unserem Raumschiff ausgehen. Hier ist gerade eine Schuss-Salve unterwegs zur ISS, was glücklicherweise aber keine negativen Auswirkungen auf dieselbe hat.

3.9.3. Spurensuche

Kehren wir zu "draw_scene" zurück. Weltall, Erde und ISS wurden gezeichnet. Die Meteore, so weit vorhanden, neu positioniert. Unsere Schüsse sind unterwegs. Nun folgt die Prozedur "draw_path":

Hier wird eine Art Kondensstreifen aufgebaut, der veranschaulicht, welchen Weg unser Raumschiff zurückgelegt hat. Die Pfadpunkte des Arrays "path_a" werden dazu in der Prozedur "path" gesetzt, welche periodisch über die Prozedur "frequencytTimer" aufgerufen wird.

Zur Anzeige des Pfades wird dann in "draw_path" einfach das "path_a"-Array durchlaufen und aus aktuellem und folgendem Punkt ein Dreieck generiert, was gemäss seiner Koordinaten als OpenGL-Grafik vom Typ "GL_TRIANGLE_STRIP" wiedergegeben wird.

Über einen Modulo-Vergleich mit der Schleifenvariablen "r" wird zusätzlich dafür gesorgt, dass die Dreiecke abwechselnd rot und grün gezeichnet werden.

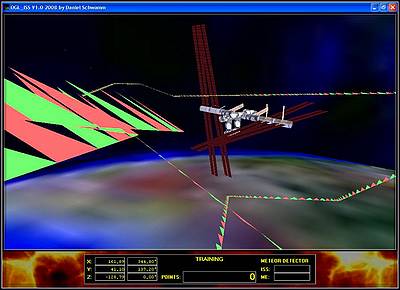
Prozedur 'draw_path': Der Weg, den unser Schiff innerhalb eines bestimmten Zeitraumes im Raum zurückgelegt hat, kann optional angezeigt werden.

3.9.4. Den Feind ins Visier genommen

Als letzte "draw_"-Aktion in "draw_scene" fehlt jetzt nur noch das Visier mit dem Fadenkreuz, welches angibt, wohin wir beim Geradeaus-Flug steuern bzw. schiessen. Diesen Job übernimmt die Prozedur "draw_visor":

Der Tiefenpuffer wird abgeschaltet, damit das Fadenkreuz nicht von weiter vorne liegenden Objekten verdeckt wird.

Anschliessend wird der OpenGL-"Malstift" 20 Meter vor uns positioniert. Dorthin wird dann das Fadenkreuz nebst einem Rahmen platziert.

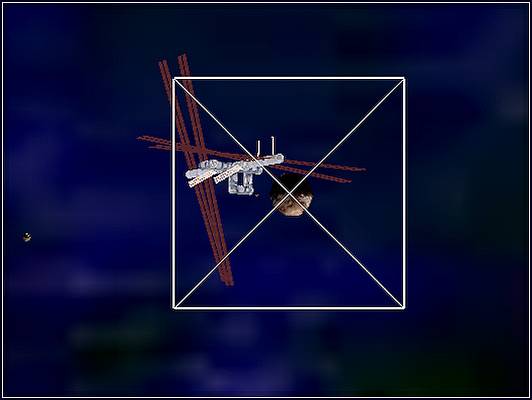
Prozedur 'draw_visor': Wiedergabe des Visiers im Cockpit unseres Raumschiffes. Hier wurde gerade ein Meteor in die Mitte genommen. Bald hat er sein Leben ausgehaucht. Und das möglichst, bevor er die ISS erreicht ...

3.9.5. Automatischer Heimflug

Ein paar Mal wurde der automatische Heimflug bereits erwähnt.

Wenn wir uns zu weit von der ISS entfernt oder die Orientierung verloren haben, dann genügt ein Druck auf die "F"-Taste, und wir werden vom Bordcomputer wieder in die Ausgangsposition direkt vor der ISS gebracht.

Obige Prozedur "flyhome" setzt den Zähler "flyhome_c" hoch.

Abschliessend werden die Positions- und Rotations-Deltas berechnet, die nötig sind, um uns aus aktueller Position und Richtung in "flyhome_c" Zeiteinheiten bis zur Start-Position zurückzuführen.

Um möglichst viele Spiel-Punkte zu ergattern, muss man sich im Spiel möglichst weit von der ISS entfernen und Meteore zerstören. Dabei sollte man gut den Meteor-Detector im Auge behalten. Einige Sekunden, bevor der losheult, kann man dann über den automatischen Heimflug rasch zur ISS zurückkehren.

Man beachte jedoch, dass, während der Bordcomputer das Kommando hat, keinerlei Aktionen des Piloten möglich sind ...

3.10. Spiel-Ende

Das Spiel ist aus, wenn ...

1. ... die "Escape"-Taste gedrückt wurde
2. ... alle Meteore zerstört sind
3. ... die ISS von einem Meteor getroffen wurde

In allen drei Fällen wird die Prozedur "game_over_show" aufgerufen:

Ist der Spiel-Level "_game_level_train" aktiv, wird über die Prozedur "game_start_show" direkt zum Start-Panel weitergeleitet.

Ansonsten wird der Level-Highscore ermittelt und gegebenenfalls mit dem aktuellen Punktestand überschrieben.

Zuletzt wird dann einfach das TPanel "gameoverp" sichtbar gemacht.

Prozedur 'game_over_show' - Fall 1: Spielende. Und diesmal war es das Ende einer erfolgreichen Schlacht.

Prozedur 'game_over_show' - Fall 2: Spielende. Du hast verloren. Und damit auch der ISS ein trauriges Ende bereitet.

4. Spiel-Impressionen

Zum Schluss noch ein paar Screenshots von "OGL_ISS" in Action:

5. Träume werden wahr

Ach ja, ich liebe OpenGL!

Als Kind hatte mich auf dem C64 nichts mehr fasziniert, als Vektor-Grafik-Spiele wie "Elite" und "Escape from Mercenary". Monatelang habe ich mich damals damit beschäftigt, deren virtuelle Welten zu erforschen. Nicht in meinen kühnsten Träumen hätte ich mir jedoch zugetraut, je auch nur etwas annähernd Ähnliches selbst programmieren zu können.

Klar, "OGL_ISS" hat bei Weitem nicht die Komplexität oder den Spielwitz der grossen Vorbilder. Aber optisch schlägt es sie allemal.

Ecken und Macken gibt es dennoch genug, obwohl "OGL_ISS" für meine Verhältnisse eigentlich ziemlich fehlerfrei geraten ist.

Die Flug-Steuerung macht manchmal nicht das, was sie tun sollte. Möglich, dass das mit dem berüchtigten "Gimbal Lock" zu tun hat - ein Problem, mit dem offenbar sogar die NASA-Ingenieure zu kämpfen haben.

Des Weiteren purzeln die Sound-Effekte gerne wüst durcheinander.

Und die Highscore-Listen - hüstel! - sind mit nur einem Eintrag je Level wahrlich auch auch mehr als bescheiden ausgefallen ...

So etwas verdirbt mir jedenfalls nicht den Spass an meinem Proggy. Ist halt nichts 100%iges. But who cares?

6. Download

"OGL_ISS" wurde mit Delphi 7 programmiert. Der komplette Source, die EXE und die Bibliotheksdatei "opengl32.dll" sind alle in diesem ZIP-Archiv verpackt:

OGL-ISS.zip (ca. 2,6 MB)

Das Original-OpenGL-Paket für Delphi habe ich von "http://www.delphigl.com" gesaugt. Das ZIP-File des Installers der Version "DGLSDK 2006.1", die ich verwendet habe, findet ihr hier:

dglsdk-2006-1.zip (ca. 8 MB)

Have fun!