OpenGL Planets - Ein Ausflug ins eigene Sonnensystem
OGL_Planets-Tutorial von Daniel Schwamm (31.03.2008)
Inhalt

Blick über den Rand der Erdscheibe: Der berühmte Holzstich von Camille Flammarion, der erst 1888 erzeugt wurde, aber im Stil des 16. Jahrhunderts angelegt wurde.
Wenn mich je ein Gebiet konstant in Bann geschlagen hat, dann die Astronomie.
Seit frühester Jugend begeistern mich Weltall, Galaxien, Sterne, Planeten, Monde,
Kometen und Asteroiden. Nicht, dass sich dadurch viel Wissen angesammelt
hätte. Muss es auch nicht; bin ja Programmierer, kein Astronom.
Trotzdem stört es mich, wenn bei den weit aus meisten Abbildungen der Planeten
die relativen Grössen und Abständen zueinander ignoriert werden. Praktisch immer
sind die Planeten viel zu dicht aneinandergedrängt und im Vergleich zur Sonne zu
gross dargestellt.
Seit meinen Uni-Tagen - inzwischen über 10 Jahre her - schleppe ich daher den Plan
mit mir herum, das Sonnensystem mit mehr Realismus auf Papier zu bringen. Nur um zu
sehen, wie die Verhältnisse wirklich sind. Doch konnte ich mich nie dazu aufraffen,
dem Gedanken Taten folgen zu lassen.
Um meinen 40sten in Ruhe zu verbringen, nahm ich mir im Januar 2008 Urlaub.
Ruhe ist aber öde. So gab ich schnell dem Impuls nach, als ich eine Dokumentation
über die Sonne sah: Mit Brockhaus und Lineal bewaffnet begann ich das Sonnensystem
schwarz auf weiss auf Papier zu bannen.
Mit Erde und Mond fing es an. Da die Erde einen Radius von 6.400 km hat, bekam
meine gemalte etwas über einem Zentimeter ab. Überrascht stellte ich fest, dass der
Mond bereits aufs nächste Blatt auszulagern war. Die 385.000 km Abstand zwischen
Erde und Mond ergaben in meiner Skala nämlich fast 40 cm. Der Mond ist echt nicht
gerade um die Ecke.

Wiedergabe des Abstandes zwischen Erde und Mond: Obwohl die Erde recht klein im linken Eck eingezeichnet ist, genügt ein einzelnes DIN A4-Blatt nicht, um darauf auch noch den Mond platzieren zu können. Es musste ein weiteres Blatt angelegt werden
Dann guckte ich mir die Daten der Sonne an. Mir war schon klar, dass die Sonne grösser
als die Erde ist. Aber dass sie gleich so ein fetter Brocken ist ...
Ihr Radius von 700.000 km zwang mich, noch ein Blatt anzulegen, wenn Erde und Sonne
den gleichen Mittelpunkt bekommen sollten. Und die Krümmung der Sonnenkugel konnte nur
angedeutet werden; mit einem handelsüblichen Zirkel satte 70 cm aufspannen ist nicht
drin.

Grösse der Sonne im Vergleich mit dem Abstand Erde zum Mond: Die Sonne ist so gross, dass in ihrem Inneren leicht das Erde-Mond-Modell Platz finden könnte. Hier sehen wir nur eine Hälfte der Sonne, benötigen aber bereits drei Din A4-Blätter. Ihre Oberfläche kann am rechten Rand nur ausschnittsweise angedeutet werden.
Okay, die Grössenverhältnisse meiner drei Spieler waren zurechtgerückt. Den Abstand
Erde-Mond hatte ich vor Augen. Jetzt suchte ich im Brockhaus nach der durchschnittlichen
Strecke zwischen Erde und Sonne. Und merkte gleich, dass ich ein Problem hatte. Ein
Riesen-Problem, gewissermassen. Denn die schwindelige Strecke von 150.000.000 km ergab
nach Adam Riese lockere 150.000.000/10.000=15.000 cm, also 150 m. So viele
Blätter hatte ich im ganzen Haus nicht.
Jetzt wollte ich es wissen. Die Sache begann Spass zu machen.
Um die Sonne komplett auf ein Din A4-Blatt zu bringen, schrumpfte ich sie weiter ein,
bis sie einen Radius von nur mehr 7 cm hatte. Mit dem Lineal zog ich eine Linie über
das erste Blatt, dann über ein zweites Blatt und drittes Blatt. Und damit hatte ich
umgerechnet gerade einmal 3 Millionen km zurückgelegt. 3 von 150 - bis zur Erde fehlten
also immer noch 50 Blätter.
Klar, 150 durch 10, macht 15 Meter. Ne, so gross ist mein Wohnzimmer nicht. Ich liess
es bleiben.

Abstände von Erde, Mond und Sonne zueinander: Bei einem Sonnen-Radius von 7 cm sind 150 Din A4-Blätter nötig, um den Abstand der Erde zur Sonne massstabsgetreu wiederzugeben. Das ist nur für Leute mit grossen Wohnungen auf Papier zu bringen.
Tja ... wie dachte ich am Anfang? Der Mond ist weit weg von der Erde? Das ist ein
Katzensprung. Die Sonne ist weit weg von der Erde. Obwohl auch das natürlich
relativ ist. Die Erde gehört den sogenannten inneren Planeten an. Richtig, richtig
weit weg sind erst die äusseren, ab Jupiter aufwärts. Für Pluto hätte ich einen
Berg von 2000 Blättern benötigt. Fast 600 Meter. Bei der ersten Skala also 6 km!
Das nun ist definitiv kein Werk mehr für das Wohnzimmer.
Und ich begann zu verstehen, warum in all den Büchern die Planetenabstände nicht
realistisch wiedergegeben wird ...
Mit Blättern wurde das nichts, das war klar. Aber Computer können mehr verdauen.
Riesen-Dimensionen spielen dort eigentlich keine Rolle; virtuell ist geduldig. Sollte
doch mit dem Teufel zu gehen, wenn ich zu dem Thema nichts im Web finden sollte.
Tja, gefunden habe ich einiges, aber nichts, was mich so richtig überzeugt hätte.
Da gab es hübsche Animationen bei YouTube etwa, die zeigten, wie gross, grösser, am
grössten schliesslich sogar die Sonne zum Zwerg wird im Vergleich zu dicken Schwestern
wie Arcturus oder Rigel.
YouTube-Video: Planets and stars in scale
Eine andere Webseite zeigt die Sonne links im Eck. Mittels Scrollbalken kann man nun
ewig weit nach rechts wandern, bis irgendwann die Erde auftauchte. Die Seite behauptet
folgerichtig, eine der breitesten im gesamten Internet zu sein.
Proportionale Repräsentation des Solarsystems bei 'devhed.com': Wer Zeit hat und auf scrollen steht ist auf dieser Webseite genau richtig.
Da OpenGL derzeit ein Steckenpferd von mir ist, googelte ich nach OpenGL-Demos des
Sonnensystems. Ein Flug von Planet zu Planet bietet sich in OpenGL doch geradezu an.
Gefunden habe ich aber nur Programme, bei denen Abstände und Grössen der Himmelskörper
logarithmisch gestaucht waren - oder überhaupt nichts mit den realen Verhältnissen zu
tun hatten.
Der Ausflug ins Web hat sich dennoch gelohnt. Denn dadurch stiess ich auf eines der
genialsten Programme, welches mir je untergekommen ist: "Stellarium". Das simuliert
ein Planetarium auf freiem Feld. Mit Nachthimmel und realitätsgetreuem Abbild der
Sternenkonstellationen. Man kann in alle Richtungen schauen und mittels Mausrad beliebig
tief ins All zoomen. Tolle Sache. Hat mich stundenlang gefesselt. Und ist Freeware!

Stellarium: Geniale Freeware, ein OpenGL-Planetarium für Sternensüchtige.
Okay, ich hatte kein für mich brauchbares OpenGL-Solarsystem im Web gefunden. Also
hiess es selbst machen. Hatte ja Urlaub. Und bevor ich es nicht wenigstens versucht
hätte, würde ich ohnehin keine Ruhe mehr finden.
Mit der Kombination Delphi und DelphiGL habe ich bereits beim Tutorial
OGL_HENRYs
gute Erfahrung gemacht. Also griff ich erneut darauf zurück. Und mit einer ersten,
leeren Delphi-Form begann die Reise, dorthin, wo noch nie ein Mensch zuvor gewesen ist ...
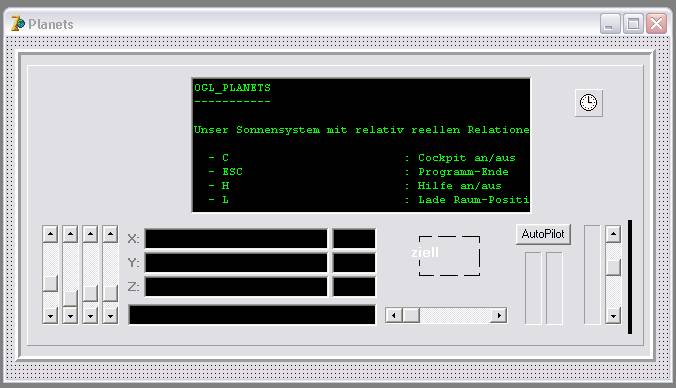
Hauptform von OGL_Planets: Hilfe-Memo, Cockpit-Instrumente & Taktgeber.
Es folgte eine laaaange Reihe von Konstanten:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
00071
00072
00073
00074
00075
00076
00077
00078
00079
00080
00081
00082
00083
00084
00085
00086
00087
00088
00089
00090
00091
00092
00093
00094
00095
00096
00097
00098
00099
00100
00101
00102
00103
00104
00105
00106
00107
00108
00109
00110
00111
00112
00113
00114
00115
00116
00117
00118
00119
00120
00121
00122
00123
00124
00125
00126
00127
00128
00129
00130
00131
00132
00133
00134
00135
00136
00137
00138
00139
00140
unit hauptu;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs,jpeg, ExtCtrls, StdCtrls, ComCtrls,inifiles,math,XPMan,mmsystem,
DGLOpenGL,SDL,SDL_Image;
const
_cap='OGL_PLANETS V1.0 (www.daniel-schwamm.de)';
_inifn='ogl_planets.ini';
_einheit='Tkm';
_rstep=10; //Rotationsschritte
_piover180=pi/180;
//Raumstaub--------------------------------
_staub_c =80000; //max Anzahl
_staub_dim =5000; //Verbreitungsdimension
_haufen_c =100; //Anzahl Staubhaufen
_haufen_dim=500; //Dimension jedes Staubhaufens
//Asteroiden------------------------------
_asteroid_c=400;
_asteroid_dim=400;
//HyperMove--------------------------------
_hypermove_len=6;
//Autopilot-------------------------------
_ap_stop = 0;
_ap_richtung =1;_ap_richtung_steps =100;
_ap_direkt =2;_ap_direkt_steps =100;_ap_direkt_distance=10000;
_ap_hmstart =3;_ap_hmstart_steps =100;
_ap_hmflug =4;_ap_hmflug_steps =100;
_ap_hmbremsen=5;_ap_hmbremsen_steps=200;
_ap_break =6;_ap_break_steps =40;
_ap_ende =7;
//Sounds----------------------------------
_snd_stop =0;
_snd_start =1;
_snd_slow =2;
_snd_fast =3;
_snd_bremsen =4;
_snd_fastbremsen=5;
_snd_break =6;
_snd_teleport =7;
//=========================================
//Sonne/Planeten/Monde---------------------
//Radius und Abstand zur Sonne in Tkm
_sonne_r = 700;
_sonne_z = 0;
_merkur_r = 2.440;
_merkur_z = 58000;
_venus_r = 6.052;
_venus_z = 108200;
//-----------------------------------------
_erde_r = 6.378;
_erde_z = 149000;
_mond_r = 2.400;
_mond_z = _erde_z-384.403;
//-----------------------------------------
_mars_r = 3.375;
_mars_z = 227000;
_deimos_r = 1;
_deimos_z = _mars_z-23.459;
_phobos_r = 1;
_phobos_z = _mars_z-9.378;
//-----------------------------------------
_ceres_r = 1;
_ceres_z = 413940;
//-----------------------------------------
_jupiter_r = 71;
_jupiter_z = 778330;
_kallisto_r = 2.41;
_kallisto_z = _jupiter_z-1882.700;
_ganymed_r = 2.631;
_ganymed_z = _jupiter_z-1070.400;
_europa_r = 1.56;
_europa_z = _jupiter_z-670.900;
_io_r = 1.8;
_io_z = _jupiter_z-421.300;
//-----------------------------------------
_saturn_r = 60;
_saturn_z = 1429400;
_saturn_ring_r = 173;
_titan_r = 2.575;
_titan_z = _saturn_z-1221.830;
_rhea_r = 1;
_rhea_z = _saturn_z-527.040;
//-----------------------------------------
_uranus_r = 25;
_uranus_z = 2870000;
_oberon_r = 1;
_oberon_z = _uranus_z-583.519;
_titania_r = 1;
_titania_z = _uranus_z-463.300;
//-----------------------------------------
_neptun_r = 24;
_neptun_z = 4504300;
_triton_r = 1;
_triton_z = _neptun_z-354.760;
//-----------------------------------------
_kuiper_r = 1;
_kuiper_z = 5500000;
//-----------------------------------------
_pluto_r = 1.2;
_pluto_z = 5913520;
_charon_r = 1;
_charon_z = _pluto_z-20;
//Sichtweite--------------------------------------------
_NearClipping=1; // Objekte ab _einheit Entfernung sichtbar
_FarClipping=-1; // sehe bis ins Unendliche
Die Sonne liegt im Ursprung des Modells, auf 0/0/0. Dann folgen wie
auf einer Perlenschnur aufgereiht die Planeten mit ihren vorgelagerten
Monden. Die Radien und mittleren Abstände zur Sonne habe ich aus
Wikipedia gefischt. Enden
lassen wir unser Solarsystem mit Pluto. Danach kommt nur noch Leere.
Anfangs habe ich versucht, alle Werte 1:1 ins Modell einzutragen, z.B. der
Sonne einen Radius von "700000000" für 700.000.000 m zu geben. Da bekam Delphi
allerdings bei den Sonnenabständen der äusseren Planeten Schluckauf. Die sprengen
irgendwelche Integer-Grenzen. Herunterskaliert auf 1:1000000 (Tkm) klappte es
dann auch mit Pluto. Nutzen wir halt den Nachkomma-Bereich für genauere
Spezifikationen.
Die Zahlen sind immer noch riesig. Der z-Achsen-Wert der Erde (Abstand zur Sonne)
beträgt immerhin 149.000 Tkm. Und Pluto? Fast 6.000.000 Tkm. Das sind keine Alltagszahlen,
das sind Zahlenmonster.
Irgendwo las ich: Alle grossen Objekte im Universum sind kugelförmig. Monde in der Form
von Kaffee-Kanne sind nicht drin, das lässt die Schwerkraft nicht zu. Und bedingt durch
den Urknall hat das Weltall selbst wohl ebenfalls eine kugelförmige Ausdehnung.
Das macht es uns einfacher, können wir doch so die meisten Objekte im Modell mit dem
gleichen OGL-Typ, nämlich "gluSphere", erzeugen.
Begonnen hatte ich mit den üblichen Verdächtigen: Sonne, Merkur, Mond, Erde, Mars,
Jupiter, Uranus, Neptun und - natürlich - Pluto, Zwergplanet hin oder her. Es kamen
aber weitere Objekte hinzu. Diverse Monde, Asteroiden und Kometen. Ausserdem konnte
man bald zwischen mehreren "All-Blasen" wählen, in denen sich alles abspielt.
Um bei dem Wust den Überblick nicht zu verlieren, deklarieren wir uns einen Index:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
//objekt-index---------------------
_inx=(
_all0,_all1,_all2,_all3,_all4,
_all5,_all6,_all7,_all8,_all9,
_sonne,
_merkur,
_venus,
_mond,
_erde,
_deimos,
_phobos,
_mars,
_ceres,
_kallisto,
_ganymed,
_europa,
_io,
_jupiter,
_titan,
_rhea,
_saturn,
_oberon,
_titania,
_uranus,
_triton,
_neptun,
_kuiper,
_charon,
_pluto,
_c
);
Die Objekte selbst werden über die Klasse "TObj" implementiert. Attribute
sind die Koordinaten im Raum, der Radius und der Name des Himmelkörpers.
Ausserdem gibt es einen Pointer für das erwähnte "gluQuadric"-Objekt.
Die Methoden "init" bzw. "destroy" erzeugen bzw. zerstören das Objekt.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
//objekt-klasse-----------------------------
tobj=class
x,y,z:double; //Koordinaten
r:double; //Radius
tx:gluint; //Textur
p:PGLUquadric; //quadric
name:string;
procedure init(nm:string;px,py,pz,pr:double);
destructor destroy;override;
end;
[...]
implementation
//===========================================================
procedure tobj.init(nm:string;px,py,pz,pr:double);
begin
name:=nm;
x:=px;y:=py;z:=pz;r:=pr;
p:=gluNewQuadric;
gluQuadricOrientation(p,GLU_OUTSIDE);
gluQuadricNormals(p,GLU_SMOOTH);
gluQuadricTexture(p,TGLboolean(true));
gluQuadricDrawStyle(p,GLU_FILL);
glEnable(GL_COLOR_MATERIAL);
hauptf.mktextur('tx_'+nm+'.jpg',tx);
end;
destructor tobj.destroy;
begin
gluDeleteQuadric(p);
glDeleteTextures(1,@tx);
inherited;
end;
Über "gluNewQuadric" wird der OGL-Typ "gluQuadric" erzeugt.
Es folgen einige "glu"-Funktionen, die "p" bestimmte Eigenschaften zuweisen.
Zum Beispiel wird der Textur-Modus aktiviert. Dadurch wird das Objekt
später nicht nur als Gittermodell wiedergegeben. Die Funktion "mktextur" läd
ein Bild von der Festplatte, wandelt dieses in eine Textur und bindet es
an das "tx"-Attribut von "TObj".
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
//lade Textur von Platte------------------------------------
procedure thauptf.mktextur(fn:string;var tx:gluint);
var
tex:PSDL_Surface;
begin
tex:=IMG_Load(pchar(hauptf.homedir+fn));
if assigned(tex) then begin
glGenTextures(1,@tx);
glBindTexture(GL_TEXTURE_2D,tx);
glEnable(GL_TEXTURE_2D);
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MIN_FILTER,GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D,GL_TEXTURE_MAG_FILTER,GL_LINEAR);
glTexParameteri(gl_texture_2d,GL_GENERATE_MIPMAP_SGIS,GL_TRUE);
glTexImage2D(GL_TEXTURE_2D,0,3,tex^.w,tex^.h,0,GL_RGB,GL_UNSIGNED_BYTE,tex^.pixels);
SDL_FreeSurface(tex);
end;
end;
Folgende Variablen werden "semi-global" in der Hauptklasse "thauptf" deklariert:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
00071
00072
00073
00074
00075
00076
00077
00078
00079
00080
00081
00082
00083
00084
//Koordinaten floats
tcoordf=Record
x,y,z:glFLoat;
end;
//Koordinaten integer
tcoord=record
x,y,z:word;
end;
//Hauptklasse------------------------------------
Thauptf = class(TForm)
[...]
public
{ Public-Deklarationen }
homedir:string;
//für OpenGL
dc:HDC;
rc:HGLRC;
//Raumpositionshalter
px,py,pz:double;
rotx,roty,rotz:double;
//Speicher Raumpositionen
sv_x,sv_y,sv_z,sv_rx,sv_ry,sv_rz:double;
//Rotations-Takt, Raumzeit-Takt
rott:double;
taktc:integer;
//quads-Objekte
leitstrahl:PGLUquadric;
saturn_ring:PGLUquadric;
//Planeten, Raumstaub, Asteroiden
obja:array[0..ord(_c)]of tobj;
stauba:array[0..ord(_staub_c)]of tcoord;
asteroida:array[0..ord(_asteroid_c)]of tcoord;
//aktuelle Höchstgeschwindigkeit
speed:double;
//HyperMove
hypermove:array[0..12,0.._hypermove_len] of tcoordf;
hypermove_tx:gluint;
//Ticker
ticker:integer;
tickerblink:byte;
tickerhint:string;
//Autopilot
ap_z:double;
ap_steps:integer;
ap_err:integer;
ap_dx,ap_dy,ap_dz:double;
ap_mark_x,ap_mark_y,ap_mark_z:double;
ap_hmmove_ok:bool;
ap_spotx:double;
//Schrift
displayliste:cardinal;
//Zeichnen-Optionen
titelok:bool;
leitstrahlok:bool;
visierok:bool;
//speed progress
speedshiftok:bool;
speedok:bool;
speedkey:word;
//Sound
snd_typ:byte;
soundok:bool;
//Funktionen
[...]
Das Array "obja" enthält unsere "TObj"-Objekte, die wir gerade implementiert haben.
Der Raum-Staub besteht aus Punkten, die im Raum angeordnet werden. Die Koordinaten
werden im Record-Typ "tcoord" gemerkt. Das muss nicht genau sein, daher reichen
Word-Werte als Speicher für x, y und z. Auch für die Positionierung der Asteroiden
genügt dieser Typ.
Der Record-Typ "tcoordf" verwendet dagegen Fliesskommazahlen. Er kommt beim
Hyper-Move-Tunnel zum Einsatz. Dieser wird mithilfe von Sinus- und Kosinus-Werten
berechnet, wie wir später sehen werden. Da dürfen die Nachkommastellen nicht
unterschlagen werden.
Das "OnCreate"-Ereignis von "TForm" nutzen wir, um unsere OGL-Umgebung
einzurichten, die Programm-Parameter aus der Initialisierungsdatei "_inifn"
einzulesen, zwei Application-Ereignisse umzubiegen, und die Cockpit-ScrollBars
auf Startposition zu setzen.
Bei Programmende ("FormDestroy") werden die Programm-Parameter auf Platte
geschrieben sowie der Speicher von allen "gluQuad"- und Textur-Objekten
gesäubert.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
00071
00072
00073
00074
00075
00076
00077
00078
00079
00080
00081
00082
00083
00084
00085
00086
00087
00088
00089
00090
00091
00092
00093
00094
00095
00096
00097
00098
00099
00100
00101
00102
00103
00104
00105
00106
00107
00108
00109
00110
00111
00112
00113
00114
00115
00116
00117
00118
00119
00120
00121
00122
00123
00124
00125
00126
00127
//----------------------------------------------------------------------------
procedure Thauptf.FormCreate(Sender: TObject);
begin
//echter Zufall
randomize;
ticker:=0;
tickerblink:=0;
tickerhint:='';
taktc:=0;
homedir:=extractfilepath(application.exename);
caption:=_cap;
//OpenGL initialisieren
DC:=GetDC(hauptp.Handle);
if not InitOpenGL then Application.Terminate;
RC:=CreateRenderingContext(
DC,
[opDoubleBuffered],
24, //farbbits
32, //tiefentest
0,0,0,
0
);
ActivateRenderingContext(DC,RC);
glDepthFunc(GL_LESS);
glenable(GL_DEPTH_TEST);
//Font und Objekte generieren
buildfont;
initobjects;
//INI-Datei einlesen
with tinifile.create(homedir+_inifn) do begin
brennweitesb.Position:=readinteger('param','brennweitesb',brennweitesb.Position);
brennweitesbChange(Sender);
allsb.Position:=readinteger('param','allsb',allsb.Position);
staubcsb.Position:=readinteger('param','staubcsb',staubcsb.Position);
rotstaubcsb.Position:=readinteger('param','rotstaubcsb',rotstaubcsb.Position);
zielsb.Position:=readinteger('param','zielsb',zielsb.Position);
speedsb.Position:=readinteger('param','speedsb',speedsb.Position);
helpm.visible:=readbool('param','helpm',helpm.visible);
titelok:=readbool('param','titelok',true);
leitstrahlok:=readbool('param','leitstrahlok',true);
visierok:=readbool('param','visierok',true);
soundok:=readbool('param','soundok',true);
sv_x:=readfloat('param','sv_x',0);
sv_y:=readfloat('param','sv_y',0);
sv_z:=readfloat('param','sv_z',_erde_z);
sv_rx:=readfloat('param','sv_rx',0);
sv_ry:=readfloat('param','sv_ry',0);
sv_rz:=readfloat('param','sv_rz',0);
free;
end;
//Hint-Nachrichten umbiegen
application.OnShowHint:=ApplicationShowHint;
//Idle-Handler umbiegen
Application.OnIdle:=IdleHandler;
//Fenstergrösse setzen
width:=640;
height:=480;
activecontrol:=nil;
//springe im Modell an Anfangsposition
pos_home;
//aktuelle Geschwindigkeit setzen
speedsbChange(nil);
//Elemente ausrichten
hauptp.Align:=alclient;
hauptbp.Align:=alclient;
cockpitp.ParentBackground:=false;
zielimgp.ParentBackground:=false;
brennweitesb.tag:=50;
speetp.Align:=alclient;
zielsb.Min:=ord(_sonne);
zielsb.Max:=ord(_pluto);
zielimg.align:=alclient;
ziell.Align:=alclient;
//Taktgeber aktivieren
taktt.tag:=_ap_stop;
taktt.enabled:=true;
self.WindowState:=wsmaximized;
end;
procedure Thauptf.FormDestroy(Sender: TObject);
var
r:integer;
begin
//INI-Datei sichern
with tinifile.create(homedir+_inifn) do begin
writeinteger('param','brennweitesb',brennweitesb.Position);
writeinteger('param','allsb',allsb.Position);
writeinteger('param','staubcsb',staubcsb.Position);
writeinteger('param','rotstaubcsb',rotstaubcsb.Position);
writeinteger('param','zielsb',zielsb.Position);
writeinteger('param','speedsb',speedsb.Position);
writebool('param','helpm',helpm.visible);
writebool('param','titel',titelok);
writebool('param','leitstrahlok',leitstrahlok);
writebool('param','visierok',visierok);
writebool('param','soundok',soundok);
writefloat('param','sv_x',sv_x);
writefloat('param','sv_y',sv_y);
writefloat('param','sv_z',sv_z);
writefloat('param','sv_rx',sv_rx);
writefloat('param','sv_ry',sv_ry);
writefloat('param','sv_rz',sv_rz);
free;
end;
//OpenGL-Umgebung freigeben
DeactivateRenderingContext;
DestroyRenderingContext(RC);
ReleaseDC(hauptp.Handle,DC);
glDeleteLists(displayliste,256);
//Objekte freigeben
for r:=ord(_all1) to ord(_c)-1 do obja[r].destroy;
end;
Beim "OGL_HENRYs"-Projekt wusste ich nichts mit dem Wert für die
Tiefen-Bits bei der OGL-Funktion "CreateRenderingContext" anzufangen. Das
Modell dort bewegt sich allerdings auch innerhalb so kleiner Dimensionen,
dass die Berechnung, welches Objekt von welchem anderen Objekt in Blickrichtung
verdeckt wird, keine Probleme darstellt.
"OGL_Planets" stösst in ganz andere Dimensionen vor. Da man im Weltall
quasi unendlich weit sehen kann, war ich gezwungen, den "Nähe-Bereich"
einzuschränken, also den Teil des Blickfeldes, ab dem Objekte direkt vor
einem zu sehen sind.
So wie ich es wollte, bekam ich es leider nicht hin. Denn eigentlich sollte
man unendlich weit sehen, gleichzeitig aber auch Objekte ab einem Meter Grösse
(im Modell ergibt das einen Wert von "0,0000001") erkennen können. Das
hätte dann sogar für die ISS im Orbit der Erde genügt.
Eine so feine Auflösung war in OGL aber nicht drin. Damit kommt offenbar der
Tiefenpuffer nicht zurecht. Der entscheidet, was vor oder hinter einem Objekt
aus Sicht des Betrachters liegt. Bei mir kam es jedoch zu Transparenz-Problemen.
Objekte tauchten plötzlich auf oder verschwanden unvermittelt wieder.
Es ist schwer, genauere Infos über den Wertebereich des Tiefen-Puffers
zu erhalten. Scheint ein Qualitätskriterium von Grafik-Karten zu sein.
Und 24 Bit sind die Obergrenze? Keine Ahnung. Meine Onboard-Grafikkarte scheint
weniger zu haben, vermutlich nur 16 Bit. Selbst nachdem das Modell so angepasst
wurde, dass Objekte erst ab Grösse "1" (also 1.000 km) aus der Nähe sichtbar
werden, erscheint die Sonne z.B. bisweilen durchsichtig.
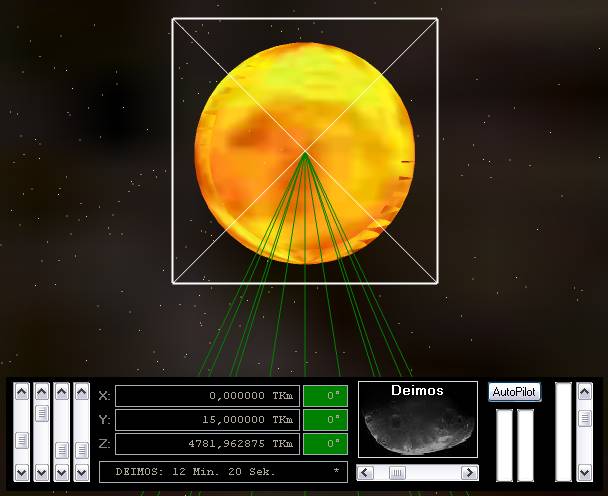
Tiefenpuffer-Problem bei OpenGL: Die Sonnen wird am Rand transparent, wenn man zu weit von ihr entfernt ist. Man sieht dann ihre Rückseite durchscheinen.
Erstaunlich mühsam war es, Schriftzüge im Modell einzubauen. OpenGL scheint
dafür keine fertige Funktion zu besitzen. Im Web wurde ich aber fündig,
fand dort etwas Source, der in die "BuildFont"-Prozedur einfloss:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
//3D-Fonts für OpenGL-Welt ----------------------------
procedure thauptf.BuildFont;
var
font:HFONT;
gmf:array[0..255] of GLYPHMETRICSFLOAT;
begin
displayliste:=glGenLists(256);
font:=CreateFont(
12, // Höhe
0, // Breite
0, // Winkel
0, // Orientierungswinkel
0, // Fett?
0, // Kursiv?
0, // Unterstrichen?
0, // Durchgestrichen?
ANSI_CHARSET, // Zeichensatz
OUT_TT_PRECIS, // Ausgabe-Präzision
CLIP_DEFAULT_PRECIS, // Clipping-Präzision (?)
PROOF_QUALITY, // Ausgabe-Qualität
FF_DONTCARE or DEFAULT_PITCH, // Family And Pitch
'Arial' // Zeichentyp
);
SelectObject(DC,font);
wglUseFontOutlines(
DC, // OpenGL-Grafik
0, // Buchstaben von
255, // Buchstaben-Anzahl
displayliste, // Die Displayliste
0.0, // Deviation From The True Outlines
0.2, // Tiefe der Schrift
WGL_FONT_LINES, // Linien-Style
@gmf // Puffer
);
end;
//Ausgabe der 3D-Schrift bei aktueller Position
procedure thauptf.glPrint(s:string);
begin
if text='' then exit;
glPushAttrib(GL_LIST_BIT);
glListBase(displayliste);
glCallLists(length(s),GL_UNSIGNED_BYTE,pchar(s));
glPopAttrib();
end;
Verstanden habe ich das nur teilweise. Offenbar wird hier ein bestimmter Bereich
in der Grafikkarte reservieren, in den die Buchstaben einmalig hinein gerendert
werden. Bei Abruf von Schrift kann dann schnell darauf zugegriffen werden. Der
im Vergleich langsame Hauptspeicher wird nicht benötigt.
Meine Onboard-Grafikkarte hat trotzdem damit zu kämpfen. So wie Schrift am Horizont
auftaucht, ruckelt das Modell. Daher wurde die Qualität der Buchstaben auf ein Minimum
reduziert. So wird z.B. ein Liniengitter genutzt, statt die Grafik aufzufüllen.
Optional kann die Schrift aber auch deaktiviert werden.
3D-Schrift: Im Modell schwebende Schriftzüge sind in OpenGL nur relativ mühsam zu genieren. Zudem sind sie auch nur kaum zu Verdauen für billige Onboard-Grafikkarten.
Nachdem in "FormCreate" die OGL-Umgebung gesetzt und die 3D-Schriften generiert wurden,
folgt nun die Initialisierung der Raum-Objekte:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
00071
00072
00073
00074
00075
00076
00077
00078
00079
00080
00081
00082
00083
00084
00085
00086
00087
00088
00089
00090
00091
00092
00093
00094
00095
00096
00097
00098
00099
00100
00101
00102
00103
00104
00105
00106
00107
00108
00109
00110
00111
00112
00113
00114
00115
00116
00117
00118
00119
00120
00121
00122
00123
00124
00125
00126
00127
00128
00129
00130
00131
00132
00133
00134
00135
00136
00137
00138
00139
00140
00141
00142
00143
00144
00145
00146
00147
00148
00149
00150
00151
00152
00153
00154
00155
00156
00157
00158
00159
00160
00161
procedure thauptf.initObjects;
function f(v:integer):integer;
begin
if v>_staub_dim then v:=v-_staub_dim;
result:=v;
end;
var
r,hr:integer;
haufena:array[0.._haufen_c] of tcoord;
i,j:integer;
begin
//HyperMove-------------------------------------------
for i:=0 to 12 do begin
for j:=0 to _hypermove_len do begin
hypermove[i,j].x:=(3-j/12)*cos(2*pi/12*i);
hypermove[i,j].y:=(3-j/12)*sin(2*pi/12*i);
hypermove[i,j].z:=-j*3;
end;
end;
mktextur('tx_hypermove.jpg',hypermove_tx);
//All-Objekte-------------------------------------------------
for r:=ord(_all1) to ord(_all9) do begin
obja[r]:=tobj.Create;
obja[r].init('all'+inttostr(r),0,0,0,1);
end;
allsbChange(nil);
//--------------------------------------------------------
leitstrahl:=gluNewQuadric;
gluQuadricOrientation(leitstrahl,GLU_OUTSIDE);
gluQuadricNormals(leitstrahl,GLU_SMOOTH);
gluQuadricDrawStyle(leitstrahl,GLU_LINE);
//---------------------------------------------------------
obja[ord(_sonne)]:=tobj.Create;
obja[ord(_sonne)].init('Sonne',0,0,_sonne_z,_sonne_r);
obja[ord(_merkur)]:=tobj.Create;
obja[ord(_merkur)].init('Merkur',0,0,_merkur_z,_merkur_r);
obja[ord(_venus)]:=tobj.Create;
obja[ord(_venus)].init('Venus',0,0,_venus_z,_venus_r);
//---------------------------------------------------------
obja[ord(_mond)]:=tobj.Create;
obja[ord(_mond)].init('Mond',0,0,_mond_z,_mond_r);
obja[ord(_erde)]:=tobj.Create;
obja[ord(_erde)].init('Erde',0,0,_erde_z,_erde_r);
//---------------------------------------------------------
obja[ord(_deimos)]:=tobj.Create;
obja[ord(_deimos)].init('Deimos',0,0,_deimos_z,_deimos_r);
obja[ord(_phobos)]:=tobj.Create;
obja[ord(_phobos)].init('Phobos',0,0,_phobos_z,_phobos_r);
obja[ord(_mars)]:=tobj.Create;
obja[ord(_mars)].init('Mars',0,0,_mars_z,_mars_r);
//---------------------------------------------------------
obja[ord(_ceres)]:=tobj.Create;
obja[ord(_ceres)].init('Ceres',0,0,_ceres_z,_ceres_r);
//---------------------------------------------------------
obja[ord(_kallisto)]:=tobj.Create;
obja[ord(_kallisto)].init('Kallisto',0,0,_kallisto_z,_kallisto_r);
obja[ord(_ganymed)]:=tobj.Create;
obja[ord(_ganymed)].init('Ganymed',0,0,_ganymed_z,_ganymed_r);
obja[ord(_europa)]:=tobj.Create;
obja[ord(_europa)].init('Europa',0,0,_europa_z,_europa_r);
obja[ord(_io)]:=tobj.Create;
obja[ord(_io)].init('Io',0,0,_io_z,_io_r);
obja[ord(_jupiter)]:=tobj.Create;
obja[ord(_jupiter)].init('Jupiter',0,0,_jupiter_z,_jupiter_r);
//---------------------------------------------------------
obja[ord(_titan)]:=tobj.Create;
obja[ord(_titan)].init('Titan',0,0,_titan_z,_titan_r);
obja[ord(_rhea)]:=tobj.Create;
obja[ord(_rhea)].init('Rhea',0,0,_rhea_z,_rhea_r);
obja[ord(_saturn)]:=tobj.Create;
obja[ord(_saturn)].init('Saturn',0,0,_saturn_z,_saturn_r);
saturn_ring:=gluNewQuadric;
gluQuadricOrientation(saturn_ring,GLU_OUTSIDE);
gluQuadricNormals(saturn_ring,GLU_SMOOTH);
//gluQuadricDrawStyle(saturn_ring,GLU_LINE);
gluQuadricTexture(saturn_ring,TGLboolean(true));
//---------------------------------------------------------
obja[ord(_uranus)]:=tobj.Create;
obja[ord(_uranus)].init('Uranus',0,0,_uranus_z,_uranus_r);
obja[ord(_oberon)]:=tobj.Create;
obja[ord(_oberon)].init('Oberon',0,0,_oberon_z,_oberon_r);
obja[ord(_titania)]:=tobj.Create;
obja[ord(_titania)].init('Titania',0,0,_titania_z,_titania_r);
//---------------------------------------------------------
obja[ord(_neptun)]:=tobj.Create;
obja[ord(_neptun)].init('Neptun',0,0,_neptun_z,_neptun_r);
obja[ord(_triton)]:=tobj.Create;
obja[ord(_triton)].init('Triton',0,0,_triton_z,_triton_r);
//---------------------------------------------------------
obja[ord(_kuiper)]:=tobj.Create;
obja[ord(_kuiper)].init('Kuiper',0,0,_kuiper_z,_kuiper_r);
//---------------------------------------------------------
obja[ord(_pluto)]:=tobj.Create;
obja[ord(_pluto)].init('Pluto',0,0,_pluto_z,_pluto_r);
obja[ord(_charon)]:=tobj.Create;
obja[ord(_charon)].init('Charon',0,0,_charon_z,_charon_r);
//---------------------------------------------------------
//Staubhaufen zufällig im Raum
for r:=0 to _haufen_c-1 do begin
haufena[r].x:=random(_staub_dim-2*_haufen_dim)+_haufen_dim;
haufena[r].y:=random(_staub_dim-2*_haufen_dim)+_haufen_dim;
haufena[r].z:=random(_staub_dim-2*_haufen_dim)+_haufen_dim;
end;
for r:=0 to _staub_c-1 do begin
if random(4)=0 then begin
//Haufen-Struktur wieder etwas auflösen
stauba[r].x:=random(_staub_dim);
stauba[r].y:=random(_staub_dim);
stauba[r].z:=random(_staub_dim);
end
else begin
//Staub um Zufallshaufen konzentrieren
hr:=r mod (_haufen_c);
stauba[r].x:=f(random(_haufen_dim)+haufena[hr].x);
stauba[r].y:=f(random(_haufen_dim)+haufena[hr].y);
stauba[r].z:=f(random(_haufen_dim)+haufena[hr].z);
end;
end;
staubcsbChange(nil);
rotstaubcsbChange(nil);
//Asteroiden
for r:=0 to _asteroid_c-1 do begin
asteroida[r].x:=random(_asteroid_dim);
asteroida[r].y:=random(_asteroid_dim);
asteroida[r].z:=random(_asteroid_dim);
end;
end;
Zuerst wird das Array des Hyper-Move-Tunnels mit Koordinaten-Werten
gefüllt. Dazu wird eine Röhre fixer Länge aus 12 Eckpunkten aufgebaut.
Dann wird die Textur geladen, die später am Röhrenmodell entlang
laufen wird, wodurch es wirkt, als würde man mit hoher Geschwindigkeit
hindurchfliegen.
Hyper-Move: Überlichtschnell durch die Röhre. Der schnellste Weg durch das Solarsystem von 'OpenGL Planets'. Nach nur wenigen Sekunden ist jedes bekannte Ziel erreicht.
Danach werden neun verschiedene "All"-Objekte generiert. Ein "All"-Objekt kann man
sich als gigantische "All-Blase" vorstellen, die unser Sonnensystem weitläufig
umschliesst. Über die "angeklebten" Texturen kann jede "All-Blase" ein individuelles
Aussehen erhalten.
Alternative Welträume: Die Textur der Hintergründe der All-Sphäre kann im Programm jederzeit gewechselt werden. Das ist zwar nicht gerade realistisch, dafür aber hübsch anzuschauen.
Man beachte, dass der Index "_all0" nicht mit einem "All"-Objekt belegt wurde.
Diese spezielle "All-Blase" ist einfach nur tiefschwarz. Und unendlich gross.
Nun ja, nicht wirklich unendlich. Wenn man lange genug in eine Richtung fliegt,
wird OGL wohl irgendwann mit einem Overflow reagieren. Habe ich aber nie
ausprobiert.
Ausgelotet habe ich dagegen die Grenzen aktivierter "All-Blasen". Selbst mit
der imaginären "Wurmloch"-Geschwindigkeit dauert es einige Minuten, bis man den
Rand erreicht hat. Das folgende Beispiel zeigt eine "All-Blase" von aussen,
aus immerhin 12-facher Pluto-Entfernung. Ein Blick auf den Bordcomputer zeigt
aber, dass die Sonne mit Lichtgeschwindigkeit in nur zwei Tagen zu erreichen
ist.
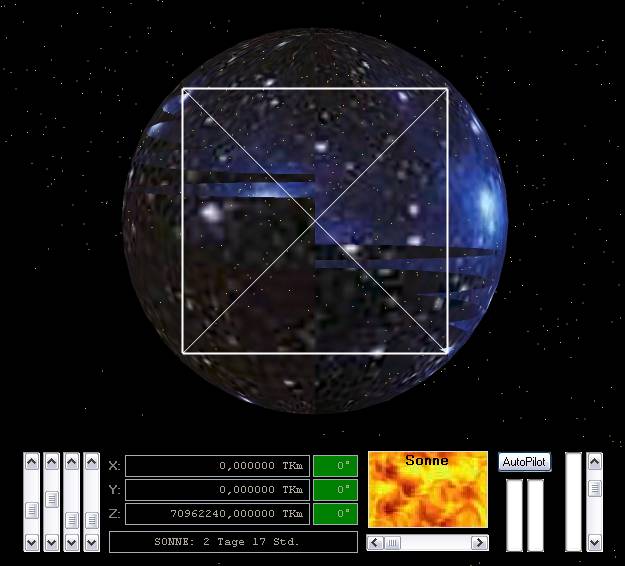
Outer Space: Wir haben uns so weit ins All vorgewagt, dass man die Grenzen unseres künstlichen Universums von Aussen sehen kann. Dennoch handelt es sich lediglich um eine virtuelle Strecke von zwei Lichttagen - ein Katzensprung im galaktischen Massstab.
Nur zum Vergleich: Unsere Milchstrasse hat einen Durchmesser 100.000 Lichtjahre.
Und Andromeda-M31, die nächste Spiral-Galaxie vor unserer Haustür, ist 2,7 Millionen Lichtjahre
von uns entfernt!
Äh ... bevor noch jemand sucht: Hinter den "All-Blasen" ist Schluss in "OGL_Planets".
Da kommt nichts mehr. Schont also euren Flieger-Finger.

Andomedagalaxie: Das der Milchstrasse nahegelegenste Sternensystem ist der Andromeda-'Nebel'. Er ist über 2.5 Millionen Lichtjahre von uns entfernt - und damit weit, weit ausserhalb der Grenzen von 'OpenGL Planets' gelegen.
Als nächste Massnahme wird der Leitstrahl initialisiert. Hierbei handelt es sich
um ein Strahlenbündel, welches im Inneren der Sonne beginnt, quer durch alle Planeten
geht und schliesslich bei Pluto endet.
Die Dimensionen im Sonnensystem sind nicht zu unterschätzen. Fliegt man unbedarft
hinein, findet man schnell seinen Heimat- oder Zielhafen nicht mehr. Das gilt
besonders jenseits von Saturn und Co., denn ab hier ist die Sonne zu klein,
um noch als Fixpunkt zur Orientierung dienen zu können. Hier hilft der Leitstrahl,
auf Spur zu bleiben.
Der Umfang des Leitstrahl-Zylinders hat die Ausmasse der Erde. So erkennt man leicht,
wie gross - oder vielmehr wie klein - der Blaue Planet im Vergleich zu manch anderen
Himmelsobjekten ist.

Leitstrahl: Im Modell kann ein Leitstrahl eingeblendet werden. Seine Dicke entspricht dem Erdumfang. Er verläuft quer durch das Solarsystem. Im Zentrum der Sonne geht es los ... fix bis zur Erde ... Saturn wird auch mitgenommen ... und endlich sind Charon & Pluto erreicht.
Nächste Aufgabe von "initObject": die Erzeugung von Sonne, Planeten und Monden.
Dazu werden "TObj"-Instanzen generiert und mit den konstanten Werten für Radius und
Sonnenentfernung gefüllt.
Zusätzlich erhalten die Objekte einen eindeutigen Namen. Dieser wird für die
3D-Beschriftung und die Objekt-Texturen benötigt.
Für Saturn wird ein zusätzliches "gluQuadric"-Objekt angelegt. Das dient später seinen
Ringen.
Nicht sonderlich aufregend, die Planeten-Bastelei. Aber wie gesagt, dank der Schwerkraft
sehen alle Himmelskörper ziemlich gleich aus. Rundlich halt. Bunte Kugeln in den
unendlichen Weiten des Raums.

Runde Himmelskörper: Egal, ob Sonne, Erde, Jupiter oder Saturn - rund dominiert. Ab einer gewissen Grösse erlaubt die Schwerkraft nichts anderes.
Okay, unser Solarsystem hat seine grossen Himmelskörper bekommen. Es folgt die Generierung
von "Staub" in einem Array. Dieser "Staub" wird später, wenn wir durch das All rasen, unser
ständiger Begleiter sein. Ausserdem kommt er beim Kometenschweif zum Einsatz. Und er rotiert
um alle grösseren Raumobjekte, gefangen von deren Gravitation.
Warum wir uns freiwillig unser Modell verdrecken? Weil es realistischer ist. Weil es gut
ausschaut. Und weil der Staub in den Tiefen des Alls ein guter Orientierungspunkt ist,
um (Eigen)Bewegung festzustellen.
Der erste "OGL_Planets"-Staub war gleichmässig verteilt. Das war mittels Zufallsgenerator
leicht zu realisieren. Wirkte aber auf die Dauer öde.
So wurde etwas "Struktur" hineingearbeitet. Der Staub sollte mal dichter, mal lichter
erscheinen. Da mir keine "Staub-Verteilungsformel" bekannt ist, bastelte ich mir etwas
zusammen.
Der "Basis-Raum" des Staubs ist ein Quader von "_staub_dim" Seitenlänge (5000) Tkm.
Er wird unterteilt in "_haufen_c" (100) Unterquader mit Kantenlänge "_haufen_dim" (500) Tkm.
Die "Unter-Quader" werden zufällig mit Raum-Staub gefüllt und sind selbst zufällig im "Basis-Raum"
verteilt. Um leere Raumbereiche zu vermeiden, wird jedes vierte Staubkorn über den gesamten
Bereich "verstreut". Insgesamt werden so "_staub_c" (80.000) Staubkörner generiert. Deren Anzahl
kann der Benutzer später on-the-fly bis auf null runter variieren. Da wird jede Putzfrau neidisch.

Raumstaub: Unser Raummodell ist nicht völlig leer. Es findet sich überall Staub, der sich wie hier im Bild zum Teil aufgrund seiner Eigengravitation örtlich verklumpt hat. Und dank dieses Staubs lassen sich Bewegungen im Raum oftmals überhaupt erst feststellen.
Zuletzt wird in der "initObjects"-Prozedur ein Array mit Asteroiden-Koordinaten
angelegt. Ähnlich wie für die Staubpartikel. Asteroiden sind jedoch grösser und
ihre Anzahl ist mit "_asteroid_c" (400) geringer. Einen "Verklumpungseffekt" gibt
es hier nicht. Die Jungs und Mädels werden einfach per Zufall über ein Gebiet von
"_asteroid_dim" (400) Tkm verteilt.
Das Asteroidenfeld befindet sich übrigens auf halber Strecke zwischen Mars und
Jupiter. Der grösste Körper, der Zwergplanet Ceres, ist Teil des Objekt-Indexes
von "OpenGL Planets" und lässt sich per Autopilot direkt ansteuern.
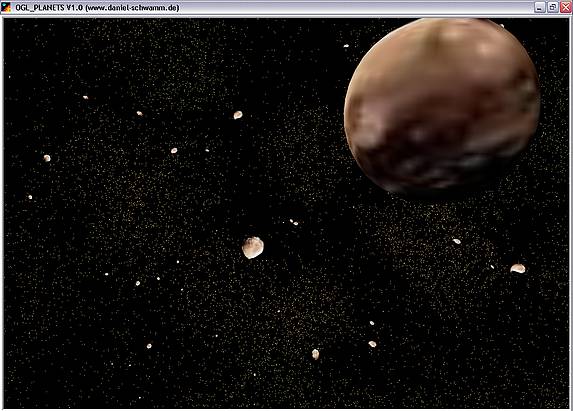
Asteroiden: Zwischen Mars und Jupiter liegt ein gewaltiges Asteroidenfeld. Hier kann man Ceres und seinen zahlreichen Kumpel einen Besuch abstatten. Im Modell wurden jedoch nur lokal begrenzt einige Hundert Asteroiden aufgenommen.

Ceres, fotografiert am 23. Januar 2004 mit dem Hubble-Weltraumteleskop: Ceres ist der grösste Brocken im Asteroidenfeld. Sie gehört mit 975 km Durchmesser bereits der Klasse der Zwergplaneten an (wie Pluto). In 'OpenGL Planets' ist sie als Navigationspunkt im Autopiloten enthalten, kann also direkt angeflogen werden.
Quelle: Wikipedia
Alle Objekte wurden erzeugt, die "initObjects"-Prozedur ist abgearbeitet. Kehren wir
zur aufrufenden Prozedur "FormCreate" zurück.
Hier wird als Nächstes das "OnShowHint"-Ereignis von TApplication auf "ApplicationShowHint" umgebogen.
Wir nutzen die Hint-Technik von Windows in gewohnter Weise. Durch obige "Zentralisierung"
können wir aber auf einheitliche Weise darauf reagieren. Aufpoppende Hint-Fenster haben
sich (bei mir) als OGL-Grafik-Killer erweisen. Kaum taucht eines auf, ruckelt das Modell.
Damit haben andere OGL-Programme ebenfalls zu kämpfen. Beispielsweise "Google Earth".
Wobei auch hier die Leistungsfähigkeit der Grafikkarte keine unerhebliche Rolle zu
spielen scheint.

Informationen durch 'Hints': Die Technik der Hints, um Informationen zu liefern, ist anschaulich. Leider sind diese aufpoppenden Fenster aber auch echte OpenGL-Killer, die gehörig auf die Performance der Grafikausgabe schlagen.
Hier nun die zentralisierte "ApplicationShowHint"-Prozedur:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
//Hints abfangen, weil die die OpenGL-Grafiken bremsen
//Hint-Texte werden stattdessen im Ticker ausgegeben
procedure Thauptf.ApplicationShowHint(
var HintStr:String;
var CanShow:Boolean;
var HintInfo:THintInfo
);
begin
tickerhint:=hintstr;
canshow:=false;
end;
Da passiert nicht viel. Wir retten den Hint-Text in "tickerhint" und sorgen mit
"canshow:=false" dafür, dass der Hint nicht als Hint erscheint. Der Text taucht
stattdessen als Laufschrift im Ticker-Band des Bordcomputers auf. Das stört
OGL nicht - und sieht cooler aus.
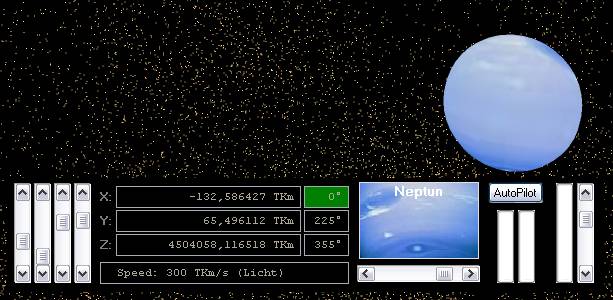
Informationen durch Laufbänder: Alle wichtigen Informationen werden in einem Laufband des Bordcomputers ausgegeben. Dadurch wird die OpenGL-Grafikausgabe nicht beeinträchtigt.
Die dafür verwendete "doTicker"-Prozedur, die ständig per Timer aufgerufen wird,
sieht folgendermassen aus:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
00071
00072
00073
00074
00075
00076
00077
00078
00079
00080
00081
00082
00083
00084
00085
00086
00087
00088
00089
00090
00091
00092
00093
00094
00095
00096
00097
00098
00099
00100
00101
00102
00103
00104
00105
00106
00107
00108
00109
00110
//--------------------------------------------------
procedure thauptf.doticker;
const
_l=35;
function fill(s:string):string;
var
i,c:integer;
begin
i:=(_l-length(s)) div 2;
for c:=0 to i-2 do s:=' '+s;
while length(s)<_l do s:=s+' ';
result:='|'+s;
end;
var
s,ss:string;
r:integer;
i,ii:int64;
d:double;
begin
if not cockpitp.visible then exit;
if tickerhint<>'' then begin
//Hint-Ereignis hat tickerhint gefüllt
s:=' *** '+fill(tickerhint);
end
else begin
r:=zielsb.Position;
d:=distance(px,py,pz,obja[r].x,obja[r].y,obja[r].z);
i:=trunc(d/speed);
if taktt.tag=_ap_stop then begin
if i=0 then begin
s:='Direktflug möglich';
end
else begin
s:='';
ii:=i div (60*60*24*365);
if ii>0 then begin
s:=s+inttostr(ii)+' Jahre ';
i:=i mod (60*60*24*365);
end;
ii:=i div (60*60*24);
if ii>0 then begin
s:=s+inttostr(ii)+' Tage ';
i:=i mod (60*60*24);
end;
if pos('Jahre',s)=0 then begin
ii:=i div (60*60);
if ii>0 then begin
s:=s+inttostr(ii)+' Std. ';
i:=i mod (60*60);
end;
if pos('Tage',s)=0 then begin
ii:=i div 60;
if ii>0 then begin
s:=s+inttostr(ii)+' Min. ';
i:=i mod 60;
end;
if pos('Std.',s)=0 then begin
if i>0 then s:=s+inttostr(i)+' Sek.';
end;
end;
end;
end;
s:=
' *** '+
fill(getspeedtxt)+
' *** '+
fill(uppercase(obja[zielsb.Position].name)+': '+s);
end
else if taktt.tag=_ap_richtung then s:='Ausrichtung'
else if taktt.tag=_ap_direkt then s:='Direktflug'
else if taktt.tag=_ap_hmstart then s:='Beschleunigung'
else if taktt.tag=_ap_hmflug then s:='Hyper-Move'
else if taktt.tag=_ap_hmbremsen then s:='Abbremsung'
else if taktt.tag=_ap_break then s:='ABBRUCH';
if pos('*',s)=0 then s:=' *** '+fill(uppercase(obja[zielsb.Position].name)+': '+s);
end;
ss:=s;
s:=copy(s,ticker+1,_l);
if length(s)<_l then s:=s+copy(ss,1,_l-length(s));
if (s<>'')and(s[1]='|') then begin
inc(tickerblink);
if tickerblink>15 then begin
tickerblink:=0;
inc(ticker);
end
else begin
s:=stringreplace(s,'|',' ',[rfreplaceall]);
if tickerblink mod 2=0 then s:='';
tickere.Text:=s;
end;
end
else begin
s:=stringreplace(s,'|',' ',[rfreplaceall]);
tickere.Text:=s;
inc(ticker);
if ticker>length(ss)then ticker:=0;
end;
end;
Zunächst wird geprüft, ob das Cockpit sichtbar ist. Falls nicht, sparen wir uns
die Arbeit und verlassen die Prozedur wieder.
Als Nächstes prüfen wir, ob in "tickerhint" ein Hint-Text zur Ausgabe
vorliegt. Normalerweise ist das nämlich nicht der Fall.
Der Hint-Text wird in modifizierter Form an die Variable "s" übergeben.
Der Ticker-Zähler "ticker" hält fest, wo im String wir uns gerade befinden,
also ab welchem Buchstaben mit der Ausgabe begonnen werden soll. Mit jedem
"Taktschlag" wird auf den nächsten Buchstaben gewechselt. Dadurch läuft der
komplette Text von rechts nach links durch "tickere".
Ist der (Hint-)Text vollständig zu sehen, was der Computer an einem bestimmten
Startzeichen (eine Pipe "|") im String erkennt, bleibt das Band stehen. Der
Text blinkt ein paar Mal (geregelt durch "tickerblink"). Dann läuft er weiter
und verschwindet im linken Rand.
Ist der Text ganz durchgescrollt, fängt die Geschichte wieder von vorne an.
Es sei denn, ein neues Hint-Ereignis wurde ausgelöst. Sind wir mit der Maus
über der OGL-Grafikausgabe gelandet, wird der Hint-Text einfach geleert.
Nun schaltet "DoTicker" um und gibt Bordcomputer-Informationen aus. U.a. wird
geprüft, ob Himmelskörper, die im Autopiloten ausgewählt wurden, per Direktflug
erreichbar sind oder ob dafür ein Sprung durch den Hyperraum nötig ist. Oder es
wird berechnet, wie lange ein Flug mit der aktuell gewählten Geschwindigkeitsstufe
dauern würde. Anders als es die (bisherige) Physik erlaubt, vermag unser
Raumschiff übrigens auch deutlich schneller zu fliegen als "nur" mit
Lichtgeschwindigkeit.

Zeit für die Strecke Erde-Sonne mit Lichtgeschwindigkeit: Laut Bordcomputer fliegen wir mit Lichtgeschwindigkeit (300.000 km/s). Die Strecke Erde-Sonne ist demnach in etwas mehr als acht Minuten zu bewältigen. Oben rechts kann man übrigens den Mond und die anvisierte Sonne erkennen.
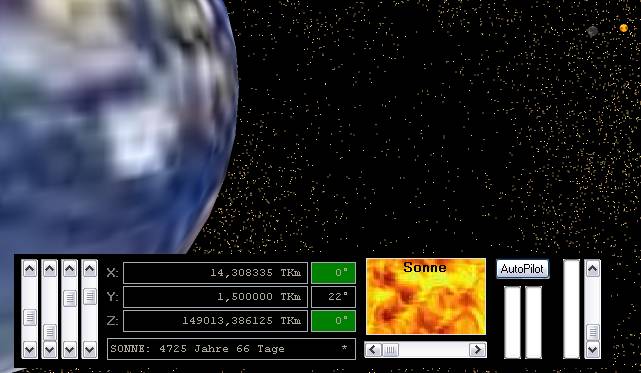
Zeit für die Strecke Erde-Sonne mit 'Spaziergeschwindigkeit': Nun fliegen wir mit 1 km/h, was in etwa der Geschwindigkeit beim Spazierengehen entspricht. Bei diesem eher gemächlichen Tempo wären wir bis zur Sonne laut Bordcomputer runde 4725 Jahre lang unterwegs. Vorausgesetzt natürlich wir laufen durch und machen niemals Pausen ...
Die dritte Variante der Anziege ist für den Autopiloten reserviert. Wird ein Ziel per
Autopilot angeflogen, werden mehrere Schritte abgearbeitet. Die Ausrichtung des
Raumschiffs muss vorgenommen werden. Es gibt eine Beschleunigungsphase. Eventuell
kommt es zum Sprung durch den Hyperspace. Abgebremst werden muss am Schluss natürlich
auch noch. Der Bordcomputer zeigt stets an, in welcher Phase wir uns befinden.
Wieder zurück in "FormCreate" fangen wir das "OnIdle"-Ereignis von "TApplication" ab.
Wann immer es ausgelöst wird, soll ein "Idle-Handler" aufgerufen werden:
00001
00002
00003
00004
00005
00006
// wenn CPU Zeit hat, wird diese Funktion aufgerufen
procedure Thauptf.IdleHandler(Sender: TObject; var Done: Boolean);
begin
draw_scene;
done:=false;
end;
Im Wesentlichen wird hier nur "draw_scene" aufgerufen. In dieser Prozedur
wird das Modell neu gerendert und zur Anzeige gebracht. Und das so oft wie
möglich. Da ist also permanente Action angesagt. Aber wir befinden uns ja
auch im Weltall, d.h. über den Wolken. Und da ist bekanntlich keine freie
Minute mehr für einen drin ...
Quatsch! Richtiger Sänger, nämlich Reinhard Mey, aber zwei Titel von ihm
vermengt. Brrr! Es ist Sonntag, ich hatte gerade eine Mütze voll Schlaf und
bin wohl noch nicht ganz wach. Sorry Reinhard ...

Sänger Reinhard Mey im Weltall: Nein, der gute Mann hat nichts, aber auch rein gar nichts mit 'OGL_Planets' zu tun. Sucht also nicht nach ihm! Ihr würdet ihn nicht finden ...
Und wieder zurück in "FormCreate". Dort bringt uns als nächster Schritt
"pos_home" auf eine fix definierte Startposition im Modell.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
//zurück zum Ursprung ------------------
procedure thauptf.pos_home;
begin
px:=0;py:=0;pz:=_erde_z;
rotx:=0;roty:=0;rotz:=0;
end;
//springe zur letzten Speicherposition
procedure thauptf.pos_load;
begin
dosound(_snd_teleport,false);
px:=sv_x;py:=sv_y;pz:=sv_z;
rotx:=sv_rx;roty:=sv_ry;rotz:=sv_rz;
sleep(1000);
end;
//merke aktuelle Raumposition-------------
procedure thauptf.pos_save;
begin
dosound(_snd_teleport,false);
sv_x:=px;sv_y:=py;sv_z:=pz;
sv_rx:=rotx;sv_ry:=roty;sv_rz:=rotz;
sleep(1000);
end;
Heimathafen ist, wie sollte es anders sein, unser schöner Blauer Planet.
Und zwar exakt in dessen Mitte. Wen das stört, der kann an den "px", "py" und
"pz"-Werten schrauben. Der Eintrag
"px:=10;" würde uns z.B. 10.000 km über dem Zentrum schweben lassen. Da die Erde
einen Radius von 6.400 km hat, befänden wir uns dann ca. 3.600 km über dem Nordpol.
"pos_home" ist mit der Leertaste verknüpft; ein Druck darauf und wir transferieren
das Raumschiff in seinen Heimathafen zurück.
Alternativ lassen sich mit "S" und "L" die Prozeduren "pos_save" und "pos_load" aufrufen.
Das speichert die aktuelle Position im Raum bzw. lädt die zuletzt gespeicherten Koordinaten.
Mh ... eine nette Idee wäre, statt "sv_x", "sc_y", "sv_z" als Einzelwerte zu deklarieren,
Arrays zu verwenden. Dann könnte man z.B. die F-Tasten verwenden, um sich mehrere
Positionen im Solarsystem zu merken. War aber zu faul, dies zu realisieren.
Weil wir schon am Ändern von Positionen sind: In "FormCreate" werden nun die
"OnChange"-Ereignisse der Cockpit-Schieberegler aufgerufen. Das bewirkt Folgendes:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
00071
00072
00073
00074
00075
00076
00077
00078
00079
00080
00081
00082
00083
00084
00085
00086
00087
00088
//----------------------------------------------------------------------
procedure Thauptf.brennweitesbChange(Sender: TObject);
var
r:integer;
begin
r:=180-brennweitesb.position;
brennweitesb.Hint:='Brennweite: '+inttostr(r)+' Grad';
brennweitesb.showhint:=true;
brennweitesb.tag:=r;
activecontrol:=nil;
formresize(sender);
end;
procedure Thauptf.allsbChange(Sender: TObject);
var
r:integer;
begin
r:=9-allsb.position;
if r=0 then allsb.Hint:='Kein Hintergrund'
else allsb.Hint:='Hintergrund tx_all'+inttostr(9-allsb.position)+'.jpg';
allsb.showhint:=true;
activecontrol:=nil;
end;
procedure Thauptf.staubcsbChange(Sender: TObject);
var
r:integer;
begin
r:=100-staubcsb.position;
r:=(_staub_c*r) div 100;
staubcsb.Hint:='Raum-Staub: '+inttostr(r);
staubcsb.showhint:=true;
staubcsb.Tag:=r;
activecontrol:=nil;
end;
procedure Thauptf.rotstaubcsbChange(Sender: TObject);
var
r:integer;
begin
r:=100-rotstaubcsb.position;
r:=(_staub_c*r) div 100;
rotstaubcsb.Hint:='Rotationsstaub: '+inttostr(r);
rotstaubcsb.showhint:=true;
rotstaubcsb.Tag:=r;
activecontrol:=nil;
end;
function thauptf.getspeedtxt:string;
var
s:string;
begin
if speedsb.Position=9 then begin s:='Laufen'; speed:=0.000001;end
else if speedsb.Position=8 then begin s:='Schall'; speed:=0.000340;end
else if speedsb.Position=7 then begin s:='Saturn V';speed:=0.011000;end
else if speedsb.Position=6 then begin s:='Komet'; speed:=0.042000;end
else if speedsb.Position=5 then begin s:='Plasma'; speed:=2.400000;end
else if speedsb.Position=4 then begin s:=''; speed:=50;end
else if speedsb.Position=3 then begin s:=''; speed:=150;end
else if speedsb.Position=2 then begin s:='Licht'; speed:=300;end
else if speedsb.Position=1 then begin s:='Warp'; speed:=1000;end
else begin s:='Wurmloch';speed:=100000;end;
if s<>'' then s:='('+s+')';
result:='Speed: '+f2s_cut(speed)+' '+_einheit+'/s '+s;
end;
procedure Thauptf.speedsbChange(Sender: TObject);
begin
speedsb.showhint:=false;
speedsb.hint:=getspeedtxt;
speedsb.showhint:=true;
activecontrol:=nil;
end;
procedure Thauptf.zielsbChange(Sender: TObject);
var
r:integer;
begin
r:=zielsb.Position;
if r<ord(_mond)then ziell.Font.Color:=clblack
else ziell.Font.Color:=clwhite;
ziell.caption:=obja[r].name;
try
zielimg.picture.LoadFromFile(homedir+'tx_'+obja[r].name+'.jpg');
except
end;
activecontrol:=nil;
end;
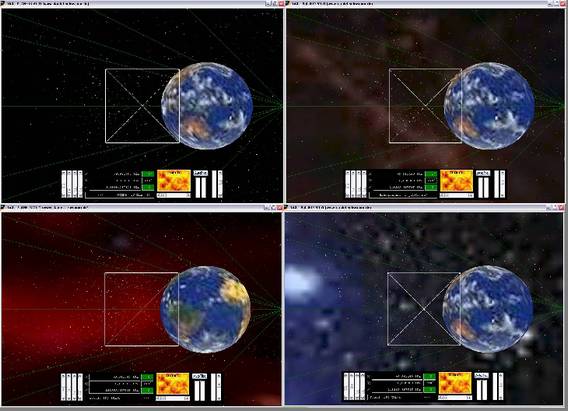
Der Schieberegler für die Brennweite beeinflusst unser Sichtfeld.
Das ist sozusagen der eingebaute "Ich-habe-mir-Drogen-eingeworfen-Wow!-Ist-das-alles-bunt-hier"-Simulator
der Schwammschen Sternenflotte. Wohl auch einer der Gründe dafür, dass sie so beliebt ist.
Bei niedriger Brennweiten wird alles gestaucht, d.h., alle Objekte erscheinen näher.
Man hat den Teleskopblick. Dann kann man z.B. die Sonne vom Saturn aus noch sehen.
Aber Vorsicht! Fliegen ist jetzt gefährlich. Objekte in der Ferne sieht man zwar,
die in unmittelbarer Nähe dagegen nicht. Aber was soll's? "OGL_Planets" kennt ja keine
Collision-Detection ...
Umgedreht bedeuten grosse Brennweiten, dass sich das Sichtfeld weitet. Das gibt Überblick
bis in die Ecken rein. Die volle Dröhnung sozusagen, den totalen Input. Nummer Fünf hätte,
wenn er denn hier leben würde, seine Freude daran.
Moment mal ... Eben merke ich selbst, dass ich Schwachsinn absondere. Zunächst mal werden
Brennweiten in Millimetern angegeben, nicht in Grad. Das trifft nur auf den Sichtwinkel zu.
Ausserdem zeigt jeder Blick auf eine Kamera, dass hohe Brennweiten Teleskop und niedrige
Brennweiten Weitwinkel bedeuten. Alles ist gerade falsch herum definiert.
Arg! Bei meiner Schusseligkeit überrascht es mich echt immer wieder, dass ich überhaupt so
etwas wie 'OpenGL Planets' auf die Reihe bekomme.
Pah! Das ist mir jetzt wurst! In meiner Welt mache ich die Regeln!

Variable Brennweiten: Ohne die Position im Raum zu ändern, sieht man durch Änderung der Brennweite einmal weniger und einmal mehr von der Umwelt. Oben links haben wir Teleskopblick, oben rechts Normalsicht ('50 Schwamm-Grad') und unten die totale Fisheye-Perspektive.
Die Konzentration von normalem Raum-Staub und von Rotationsstaub kann über zwei Schieberegel
im Cockpit gesondert variiert werden.
Gearbeitet wird stets mit dem gleichen Raum-Staub-Array, das wir in "initObjects" gefüllt
haben. Es wird nur die Obergrenze geändert, die festlegt, wie viele der 80.000 Staubpartikel
jeweils angezeigt werden sollen.
Ursprünglich hatte ich das Staub-Array jedes Mal neu erzeugt. Das kostete aber Zeit und änderte
das "Staubbild" sprunghaft, bedingt durch die neuen Zufallswerte. So brauchen wir zwar etwas
mehr Speicherplatz, die Übergänge sind aber viel fliessender. Ganz so, als würde man sich
einfach eine schärfere Brille anziehen.
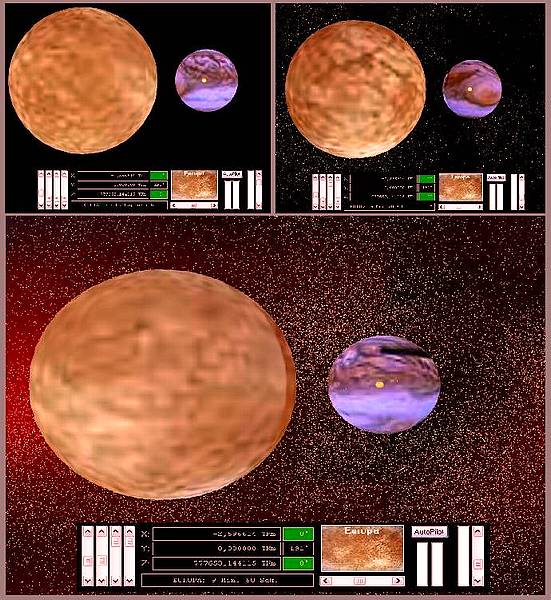
Variabler Staub: Wir befinden uns beim Mond Europa. Im Hintergrund ist der gewaltige Jupiter zu erkennen. Oben links ist das All noch keimfrei, oben rechts ist Raumstaub dazu gekommen, und unten zusätzlich auch noch Rotationsstaub. Da schwirrt uns ein Haufen Zeugs um die Ohren.
Und noch einmal in "FormCreate" zurück. Wir machen jetzt den "Zeitgeber" scharf,
den "Taktschlag" unseres Universums. Der TTimer "taktt" feuert alle 50 Millisekunden
sein "OnTimer"-Ereignis ab. Sämtliche Synchronisationsprozesse in "OGL_Planets"
laufen darüber ab. Weitere Timer sind daher nicht nötig.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
00071
00072
00073
00074
00075
00076
00077
00078
00079
00080
00081
00082
00083
00084
00085
00086
00087
00088
00089
00090
00091
00092
00093
00094
00095
00096
00097
00098
00099
00100
00101
00102
00103
00104
00105
00106
00107
00108
00109
00110
00111
00112
00113
00114
00115
00116
00117
00118
00119
00120
00121
00122
00123
00124
00125
00126
00127
00128
00129
00130
00131
00132
00133
00134
00135
00136
00137
00138
00139
00140
00141
00142
00143
procedure Thauptf.takttTimer(Sender: TObject);
function getflugstep:double;
begin
result:=speed/speedpb.max;
result:=2*taktt.interval/1000*result;
result:=speedpb.position*result;
end;
var
w,d:double;
r,schiefe:integer;
pstep:double;
begin
inc(taktc);if taktc>360 then taktc:=0;
rott:=getangle(rott-0.5);
doticker;
if taktt.tag=_ap_stop then begin
if speedok and(speedpb.Position=0) then begin
dosound(_snd_start,true);
end;
if speedok and(speedpb.Position=speedpb.max) then begin
dosound(_snd_slow,true);
end;
if not speedok and(speedpb.Position>0) then begin
dosound(_snd_bremsen,false);
end;
if speedok then begin
speedpb.Position:=speedpb.Position+1;
end
else begin
speedpb.Position:=speedpb.Position-1;
end;
if speedpb.Position=0 then begin
dosound(_snd_stop,false);
end;
if speedshiftok then begin
pstep:=speedpb.position*_rstep/speedpb.max;
if speedkey=vk_up then begin
rotx:=getangle(rotx-pstep);
end
else if speedkey=vk_down then begin
rotx:=getangle(rotx+pstep);
end
else if speedkey=vk_left then begin
rotz:=getangle(rotz-pstep);
end
else if speedkey=vk_right then begin
rotz:=getangle(rotz+pstep);
end;
end
else if speedkey=vk_up then begin
pstep:=getflugstep;
px:=px-sin(roty*_piover180)*pstep;
pz:=pz-cos(roty*_piover180)*pstep;
end
else if speedkey=vk_down then begin
pstep:=getflugstep;
px:=px+sin(roty*_piover180)*pstep;
pz:=pz+cos(roty*_piover180)*pstep;
end
else if speedkey=vk_left then begin
pstep:=speedpb.position*_rstep/speedpb.max;
roty:=getangle(roty+pstep);
end
else if speedkey=vk_right then begin
pstep:=speedpb.position*_rstep/speedpb.max;
roty:=getangle(roty-pstep);
end
else if speedkey=vk_prior then begin
pstep:=getflugstep;
py:=py+pstep;
end
else if speedkey=vk_next then begin
pstep:=getflugstep;
py:=py-pstep;
end;
speedok:=false;
draw_scene;
exit;
end;
//Autopilot-Flug-Modus
case taktt.Tag of
_ap_stop : ;
_ap_richtung : ap_richtung;
_ap_direkt : ap_direkt;
_ap_hmstart : ap_hmstart;
_ap_hmflug : ap_hmflug;
_ap_hmbremsen: ap_hmbremsen;
_ap_break : ap_break;
_ap_ende : ap_ende;
end;
if(taktt.Tag=_ap_hmstart)or(taktt.Tag=_ap_hmflug)then begin
//Autopilot und Spot aktiv
//Spot genau in Mitte?
schiefe:=round(rotz);
if(schiefe=0)or(schiefe=360)then begin
//Neuinitialisierung eines Fehlerterms
if random(2)=1 then d:=1 else d:=-1;
rotz:=getangle(1*d*_rstep/2);
end;
if rotz<180 then begin
//Ebene links unten
w:=rotz;
d:=-1
end
else begin
//Ebene rechts unten
w:=360-rotz;
d:=1;
end;
//variiere Spot-Tempo in gegebener Richtung
d:=(random(10)+1)*w*d/200;
ap_spotx:=ap_spotx+d;
//Fehler zu gross?
if abs(ap_spotx)>2 then begin
//Autopilot abbrechen
ap_steps:=_ap_break_steps;
taktt.tag:=_ap_break;
for r:=20 to 30 do begin
windows.Beep(r*2,r div 5);
end;
end
else if abs(ap_spotx)>1 then begin
//Warnung
windows.Beep(100,100 div 5);
end;
end;
end;
Bei jedem Taktschlag ändern sich zwei globale Zähler, "taktc" und
"rott". Beide bewegen sich im Interval 0-360 (Grad). "taktc" kommt beim
Hyper-Move und dem Kometen-Staub zum Einsatz. Über "rott" lassen wir in
"draw_scene" die Planeten um ihre eigene Achse rotieren.
Anschliessend rufen wir "doTicker" auf. Die Prozedur kennen wir ja schon.
Wir prüfen weiter, ob "taktt.tag=_ap_stop" gilt. Wenn ja, ist der Autopilot nicht
aktiv und das Raumschiff kann über Tastatur gesteuert werden. Die Tasten für
Flug- und Richtungsänderungen modifizieren globale Variablen, die hier erst
interpretiert werden.
Wird etwa die "Cursor hoch"-Taste dauerhaft gedrückt, hat die Globale "speedok" den Wert
"TRUE". Das wiederum bewirkt, dass sich die Position der TProgressBar "speedpb" bei
jedem Taktschlag so lange erhöht - und damit die Fluggeschwindigkeit unseres Raumschiffs -,
bis sie ihr Maximum erreicht hat. Wird die "Cursor hoch"-Taste losgelassen, ändert sich
"speedok" auf "FALSE". Die Folge ist, dass die "speedpb" absteigende Werte annimmt,
das Raumschiff wird allmählich langsamer, bis es schliesslich stillsteht.
Mh ... natürlicher wäre es für ein Weltraum-Fluggerät ja gewesen, keine Bremsphase
einzubauen. Einmal beschleunigt flöge es, bis es durch eine gegenläufige Beschleunigung
wieder abgebremst würde. Bei der Rotations das Gleiche - einmal angestossen, dreht es
sich, dreht es sich, dreht es sich.
Tja, zu spät dran gedacht, der Zug ist abgefahren.
Ein Lob hat die Steuerung allerdings verdient: Die Änderung der Positionsvariablen in
Flugrichtung ist systemunabhängig. Der Universums-Takt arbeitet nämlich auf allen Rechnern
mit dem gleichen Tempo. So können Flugsekunden mittels "getflugstep()" umgerechnet werden,
sodass sie "wirklich" eine Sekunde lang sind. Egal, wie schnell die Tastatur reagiert,
wie rasch die Szenerie gerendert wird oder wie oft und fest "Cursor hoch" gedrückt wird,
die angegebene Maximal-Geschwindigkeit bleibt davon unbeeinflusst.
Der zweite Teil des Taktgebers kommt zum Einsatz, wann immer der Autopilot aktiv ist.
Über "taktt.tag" erfahren wir, in welcher Phase er sich gerade befindet.
Befinden wir uns im Hyper-Move-Modus, dann wird jetzt die Position des "Spots" zufällig
variiert. Der "Spot" befindet sich idealerweise in der Mitte eines "grünen Bereichs".
Der kleine Fiesling neigt aber dazu, in den "roten Bereich" zu wandern. Gelingt ihm das,
hat das üble Folgen: Der Autopilot bricht ab - und unser Raumschiff schiesst unsanft
aus dem Hyper-Move-Tunnel heraus.
Aufgabe des Piloten ist es also, durch geschickte Links-Rechts-Steuerungen während des
Hyper-Moves den "Spot" möglichst in der Mitte des grünen Bereichs zu halten. Dabei werden
auch schon kleine Abweichungen bestraft: Sie erhöhen eine Art "Strafkonto", dessen Wert
in die Flugvariablen derart einfliesst, sodass das Ziel nicht mehr mit 100%iger Genauigkeit
getroffen wird; manchmal rauscht man so leicht ein paar Hunderttausend Kilometer
am anvisierten Planeten vorbei.
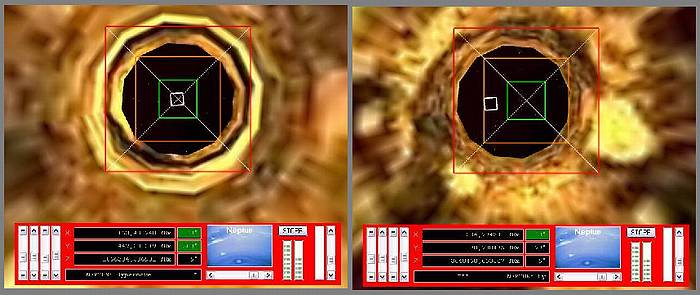
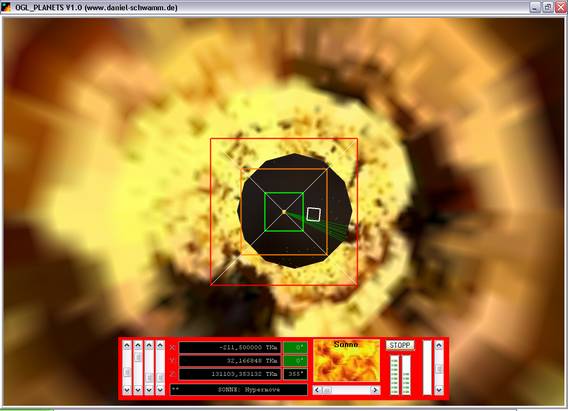
Spiel mit dem 'Spot' während eines Hyper-Move-Fluges: Im linken Bild befindet sich der 'Spot', so wie es sich gehört, innerhalb des grünen Bereichs. Rechts dagegen sieht es gar nicht gut für uns aus - gleich fallen wir aus dem Hyper-Move-Tunnel.
Anfänger fallen oft aus dem Hyperspace. Fortgeschrittene kommen
zwar meistens durch, verfehlen durch ihr angesammeltes Strafkonto durch leichte
Fehlsteuerungen ihr Ziel aber dennoch. Gute Piloten dagegen schaffen es sogar bis
in den Zielplaneten hinein!
Exakt in der Mitte bin ich selbst ja noch nie gelandet. Vermutlich ist das gar nicht
möglich (Hey, ich hab es programmiert. Sollte ich da so etwas nicht wissen?). Es sei
denn, der Zufallsgenerator spuckt zufällig eine Serie von ausschliesslich Null-Werten
aus. Das aber wäre kein Können, sondern Zufall.
Ein letztes Mal kehren wir zur "FormCreate"-Prozedur zurück. Dort bleibt noch ein
einziger wichtiger Job zu tun, nämlich die Ausgabeform zu maximieren. Das wiederum
löst das "FormResize"-Ereignis aus:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
procedure Thauptf.FormResize(Sender: TObject);
var
v:double;
begin
//Hilfefenster zentrieren
helpm.width:=hauptp.width div 2;
helpm.height:=hauptp.height-hauptp.height div 3;
helpm.Left:=(hauptp.width-helpm.Width)div 2;
helpm.top:=(hauptp.height-helpm.height)div 2-40;
//Cockpit zentrieren
cockpitp.Left:=(hauptp.width-cockpitp.Width)div 2;
cockpitp.top:=(hauptp.height-cockpitp.height)-10;
//OpenGL-Adaptionen
glViewport(0,0,hauptp.ClientWidth,hauptp.ClientHeight);
glMatrixMode(GL_PROJECTION);
glLoadIdentity;
v:=hauptp.ClientWidth/hauptp.ClientHeight;
gluPerspective(brennweitesb.tag,v,_NearClipping,_FarClipping);
glMatrixMode(GL_MODELVIEW);
Draw_Scene;
end;
Hier werden ein paar Delphi-Komponenten auf dem Bildschirm zurechtgerückt. Und über
den OGL-Befehl "gluPerspective" neben der Brennweite auch angegeben, ab welcher
Entfernung Objekte im Modell zu sehen sind ("_NearClipping") bzw. ab wann sie
nicht mehr zu sehen sind ("_FarClipping").
Weiter oben hatte ich schon erwähnt, dass ich mit diesen Werten Probleme hatte,
da leider so etwas wie "von null bis Unendlich" in OpenGL technisch nicht möglich
zu sein scheint.
Die Konstante "_NearClipping" bekommt den Wert "1". Im Modell bedeutet dies,
dass Objekte erst dann sichtbar werden, wenn man mindestens 1.000 km von ihnen
entfernt ist. Nähert man sich ihn weiter, werden sie transparent, verschwinden
also einfach. Wir sind also gezwungen, alle wichtigen Objekte mindestens 1000 km
gross zu machen. Bedingt dadurch entsprechen einige Himmelsobjekte nicht ihren
wahren Ausmassen. Dazu gehören die Asteroiden genauso wie eine Reihe von Monden,
die in der Wirklichkeit kleiner sind.
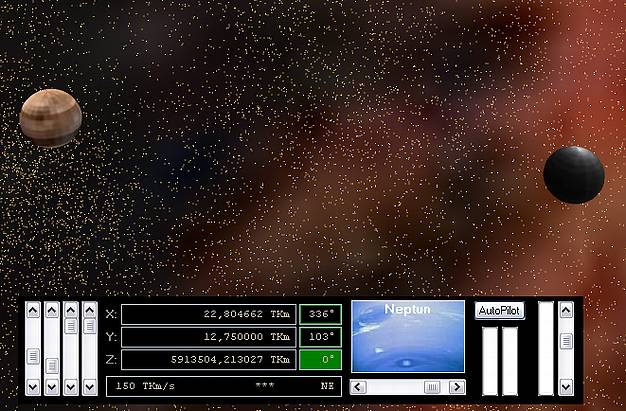
Charon künstlich vergrössert: Aufgrund technischer Gegebenheiten musste der Mond von Pluto, Charon, grösser dargestellt werden, als er tatsächlich ist. Ansonsten würde er nämlich beim Näherkommen einfach verschwinden. Im wirklichen Leben würde er etwa gerade einmal halb so gross wie der Pluto erscheinen (was für einen Mond allerdings immer noch ziemlich gross ist im Vergleich zu seinem Planeten).
Im Weltall kann man praktisch unendlich weit sehen. Daher hat "_FarClipping" den
Wert "-1" erhalten. Negative Werte sind hier eigentlich nicht erlaubt, aber
meine OGL-Version schluckt es klaglos. Mh ... ein Wert von z.B. "10*_pluto_z" wäre
allerdings exakter gewesen.
Die Clipping-Werte beeinflussen offenbar den Tiefenpuffer, der ja prüfen soll,
welche Objekte vor welchen anderen Objekten in Sichtrichtung liegen. In "OGL_Planets"
haben sich damit so manche Probleme ergeben (siehe Abschnitt "Tiefergehende Probleme").
Im Web fand ich bei http://www.opengl.org
folgende Formel zu den Bits des Tiefenpuffers bei gegebenen Clipping-Werten:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
Es sei:
_pluto_z = 5913520;
_NearClipping = 1;
_FarClipping = 10*_pluto_z;
Dann gilt:
lost_bits := log2(_FarClipping/_NearClipping);
'roughly log2(_FarClipping/_NearClipping) bits of depth buffer precision are lost'
Bei mir ergibt das: lost_bits = log2(59135200) =7,77 ~ 8
Doch was sagt das aus?
Mh ... mal angenommen, der Tiefenpuffer hat 16 Bits. Dann blieben 16 - 8 = 8 Bits
"Präzision" übrig. Damit kann man bekanntlich einen Wertebereich von 0-255 abdecken.
Heisst das, dass man über den Tiefentest bei zwei Objekten, die mehr als 255 "Einheiten"
voneinander entfernt sind, nicht mehr entscheiden kann, wer auf der z-Achse vor dem
anderen liegt?
Bei 24 bit Tiefenpuffer stünden 16 Bits "Präzision" zur Verfügung. Das ergibt einen
Wertebereich von immerhin 0 bis 65535 "Einheiten".
Aber egal, beide Varianten passen bei "OGL_Planets" nicht so recht. Die ersten
Transparenz-Effekte sieht man z.B. bei der Sonne ab einem Abstand von 3.500 "Einheiten".
Das liegt weder in der Nähe des 255er- noch des 65535er-Grenzwertes ...
Da soll nun einer schlau daraus werden.
Vergessen wir den Ärger mit dem Tiefenpuffer. Freuen wir uns lieber, dass die
"FormCreate"-Prozedur endlich abgearbeitet ist. "OGL_Planets" ist nun bereit,
sichtbare Ergebnisse auf dem Bildschirm auszuwerfen. Nötig ist dazu nur ein
wenig Idle-Time der CPU oder ein universaler Taktschlag von "taktt" ...
... es sei denn, der Benutzer ist schneller und drückt vorher eine beliebige Taste.
Dann wird nämlich erst folgende Prozedur abgearbeitet:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
00071
//------------------------------------------------------------------------
procedure Thauptf.FormKeyDown(Sender: TObject; var Key: Word;
Shift: TShiftState);
var
i:integer;
begin
speedok:=false;
//Autopilot aktiv?
if taktt.tag<>_ap_stop then begin
//ja: Tastatur aktiv?
if
(taktt.tag<>_ap_richtung)and
(taktt.tag<>_ap_hmbremsen)
then begin
if key=vk_right then begin
rotz:=getangle(rotz-_rstep);
end
else if key=vk_left then begin
rotz:=getangle(rotz+_rstep);
end;
end;
exit;
end;
//Shift gedrückt?
speedshiftok:=(ssctrl in shift);
//irgendeine Steuertaste gedrückt?
if
(key=vk_right)or(key=vk_left)or
(key=vk_prior)or(key=vk_next)or
(key=vk_up)or(key=vk_down)
then begin
speedok:=true;
if speedpb.position=0 then speedkey:=key
else if speedkey<>key then speedok:=false;
exit;
end;
//Tempoauswahl per 0-9
if(key>=ord('0'))and(key<=ord('9'))then begin
i:=key-ord('0');
if i=0 then i:=9 else dec(i);
speedsb.position:=speedsb.max-i;
end
//Tempoauswahl mit + und -
else if key=107 then begin //+
speedsb.position:=speedsb.Position-1;
speedsbChange(Sender);
end
else if key=109 then begin //-
speedsb.position:=speedsb.Position+1;
speedsbChange(Sender);
end
//Sonstiges
else if key=vk_space then pos_home
else if key=ord('L') then pos_load
else if key=ord('S') then pos_save
else if key=ord('M') then soundok:=not soundok
else if key=ord('T') then titelok:=not titelok
else if key=ord('H') then helpm.Visible:=not helpm.Visible
else if key=ord('C') then cockpitp.Visible:=not cockpitp.Visible
else if key=ord('O') then leitstrahlok:=not leitstrahlok
else if key=ord('V') then visierok:=not visierok
else if key=vk_escape then close;
end;
Zu Beginn wird geprüft, ob der Autopilot aktiv ist. Wenn ja, wird geprüft,
ob das Raumschiff gerade auf sein Ziel ausgerichtet ("_ap_richtung") oder
abgebremst ("_ap_hmbremsen") wird. In diesen Fällen werden Tastatureingaben
ignoriert. Ansonsten werden "Cursor links"- und "Cursor rechts"-Ereignisse
abgefragt, da diese unseren Flug durch den Hyperraum steuern.
Sei der Autopilot nicht aktiv. Dann wird geprüft, ob eine Taste gedrückt wurde,
die eine Positionsänderung des Raumschiffs bewirkt. Wenn ja, werden die passenden
globalen Variablen modifiziert. Wir wir bereits gesehen haben, beeinflusst das
wiederum den Steuerungsmechanismus in "takttTimer". Anschliessend wird die Prozedur
verlassen.
Wurde keine Steuertaste gedrückt, bleibt zu prüfen, ob eine der anderen,
im Hilfeschirm beschriebenen Tasten betätigt wurde. Die Taste "H" bringt
uns zur Erde zurück, "C" schaltet das Cockpit an bzw. aus, "S" speichert
die aktuelle Position auf Platte usw.
Kaum hat die CPU "Freizeit", wird über das "OnIdle"-Ereignis die Prozedur "draw_scene"
aufgerufen (siehe Abschnitt "'Carpe diem' - nutze den Tag!"). Hier endlich nimmt unser
Universum Gestalt an:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
//------------------------------------------------------------------
procedure thauptf.draw_scene;
procedure wrrot(ed:tedit;rot:integer);
var
s:string;
begin
if rot mod 90=0 then ed.Color:=clgreen
else ed.color:=clblack;
s:=inttostr(rot);
while length(s)<4 do s:=' '+s;
ed.Text:=s+'°';
end;
procedure wrp(ed:tedit;p:double);
var
s:string;
begin
s:=f2s(p)+' '+_einheit;
while length(s)<25 do s:=' '+s;
ed.Text:=s;
end;
begin
//Bildpuffer komplett löschen
glClear(GL_COLOR_BUFFER_BIT OR GL_DEPTH_BUFFER_BIT);
glLoadIdentity;
//Drehung um x/y/z-Achsen
glRotatef(360-rotx,1.0,0,0);
glRotatef(360-roty,0,1.0,0);
glRotatef(360-rotz,0,0,1.0);
if cockpitp.visible then begin
wrrot(rotxe,trunc(rotx));
wrrot(rotye,trunc(roty));
wrrot(rotze,trunc(rotz));
end;
//aktuelle Position im Raum
glTranslatef(-px,-py,-pz);
if cockpitp.visible then begin
wrp(pxe,px);
wrp(pye,py);
wrp(pze,pz);
end;
draw_all;
draw_leitstrahl;
draw_planets;
draw_staub;
draw_hypermove;
draw_fadenkreuz;
SwapBuffers(DC);
end;
Zuerst wird der Bild- und Tiefenpuffer gelöscht. Der virtuelle OGL-Zeichenstift wird
über "glLoadIdentity" in den Ursprungs-Zustand gebracht.
Danach rotiert und verschiebt sich das Modell zur aktuellen Position. Die zugehörigen
Werte stehen in den globalen Variablen für die Rotation "rotx", "roty" und "rotz",
sowie den globalen Variablen für die Position "px", "py" und "pz". Sie werden im
Cockpit in formatierter Weise ausgegeben.
Anschliessend werden diverse "draw_"-Prozeduren aufgerufen, die wir uns gleich
ansehen werden.
Zuletzt wird die ganze Szenerie mittels "SwapBuffer" auf den Bildschirm angezeigt.
Wie bereits beschrieben, wird unser Solarsystem von einer "All-Blase" umschlossen.
Gerendert wird diese Sphäre über die Prozedur "draw_all":
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
//all-------------------------------------------------
procedure thauptf.draw_all;
var
b:byte;
begin
//hole aktive All-Signatur
b:=9-allsb.position;if b=0 then exit;
glPushMatrix();
//Tiefentest für All-Blase aus, da sonst sonne transparent
//(vermutlich wird 24-bit-Bereich des Tiefenpuffers überschritten)
gldisable(GL_DEPTH_TEST);
glTranslatef(obja[b].x,obja[b].y,obja[b].z);
glRotatef(90,1,0,0);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D,obja[b].tx);
gluSphere(obja[b].p,3*_pluto_z,20,20);
glDisable(GL_TEXTURE_2D);
//tiefentest wieder aktiv
glenable(GL_DEPTH_TEST);
glPopMatrix();
end;
Die Nummer der aktiven "All-Blase" ergibt sich aus "9" minus der Position der
ScrollBar "allsb". Dadurch wird der Zahlenbereich von 0 bis 9 bzw. der definierte
Index-Bereich "_all0" bis "_all9" abgedeckt. Insgesamt können also 10
verschiedene Hintergründe ausgewählt werden, wobei eine Stufe einem leeren Hintergrund
entspricht.
Die Umrechnung mit der "9" dient dazu, Minimum und Maximum von "allsb" umzukehren.
Anders als von Borland vorgesehen, liefert "allsb" so den kleinsten Wert, wenn der
Schieberegler ganz unten ist. Das gefiel mir besser.
Wurde "_all0" gewählt, ist nichts weiter zu tun. Es wird keine "All-Blase" gemalt,
der Hintergrund bleibt schwarz, wir verlassen die Prozedur wieder.
Ansonsten wird der Tiefentest deaktiviert. Davon versprach ich mir eine
Besserung der Transparenz-Probleme. Da sich im Normalfall nichts hinter der
"All-Blase" befindet, kann sie beim Tiefentest unberücksichtigt bleiben.
Viel Besserung hat das aber nicht gebracht.
Der Mittelpunkt der "All-Blase" wird auf "0/0/0" gesetzt. Er ist also identisch mit
dem der Sonnen. Nur ist die "gluSphere", die wir dann zeichnen, erheblich grösser
als die Sonnen-Sphäre (die ihrerseits schon gewaltig ist).
Zuletzt wird der Tiefentest wieder aktiviert und zu "draw_scene" zurückgekehrt.
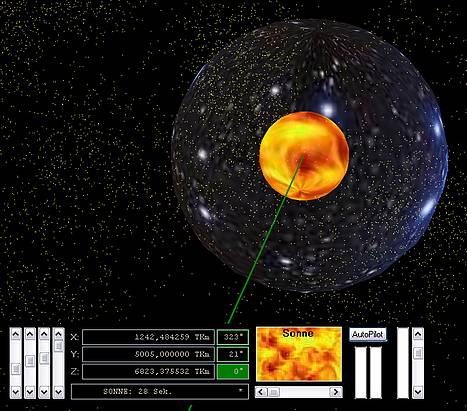
Sphäre des Weltalls herunterskaliert: Die hier gezeigte 'All-Blase' bekam einen kleineren Radius verpasst, um zu demonstrieren, dass sich ihr Ursprung mit dem der Sonne deckt.
Als Nächstes wir der Leitstrahl erzeugt:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
//Distanz zwischen zwei Punkten------------------------------
function thauptf.distance(x1,y1,z1,x2,y2,z2:double):double;
begin
result:=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)+(z1-z2)*(z1-z2));
end;
//Leitstrahl-------------------------------------------
procedure thauptf.draw_leitstrahl;
var
abstand:double;
begin
if not leitstrahlok then exit;
abstand:=distance(
px,py,pz,
obja[ord(_sonne)].x,obja[ord(_sonne)].y,obja[ord(_sonne)].z
);
if(abstand>2*_pluto_z) then exit;
glPushMatrix();
glTranslatef(obja[ord(_sonne)].x,obja[ord(_sonne)].y,obja[ord(_sonne)].z);
glColor3f(0.0,0.5,0.0);
gluCylinder(leitstrahl,_erde_r,_erde_r,_pluto_z,12,1);
glColor3f(1.0,1.0,1.0);
glPopMatrix();
end;
Zuerst wird geprüft, ob der Leitstrahl aktiv ist. Ist dem nicht so,
verlassen wir die Prozedur gleich wieder.
Anschliessend berechnen wir über die "distance"-Funktion unseren aktuellen
Abstand zum Startpunkt des Leitstrahls (identisch mit dem Ursprung der Sonne).
"Distance" basiert übrigens auf dem ins Dreidimensionale übertragenem Satz
von Pythagoras (mehr dazu im Abschnitt "Wie finde ich mein Ziel in den Weiten des Alls?"):

Pythagoras als Astronaut: Unser Copilot, der Grieche Pythagoras, hilft uns dabei, den Abstand zwischen zwei gegebenen Punkten im Raum zu ermitteln.
Befinden wir uns mehr als zwei Pluto-Strecken vom Leitstrahl entfernt, wird
er nicht mehr gezeichnet. Wir verlassen die Prozedur.
Ansonsten platzieren wir den OGL-Malstift auf den Ursprung, färben ihn mit "glColor"
grün ein, und erzeugen über "gluCylinder" ein zylindrisches Bündel aus 12 Strahlen,
die einen Radius von "_erde_r" haben sowie eine Länge von "_pluto_z".
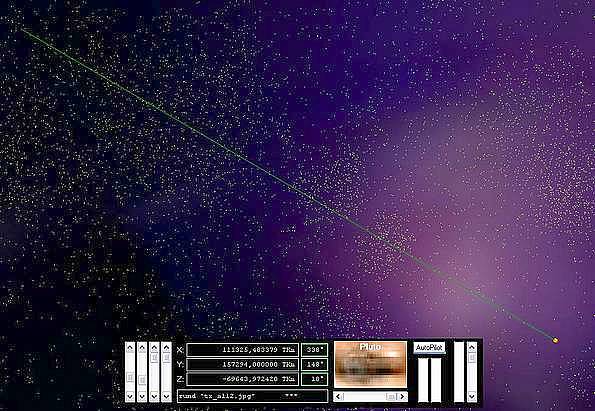
Leitstrahl durch das Solarsystem: Bei genügend Abstand ist der Leitstrahl in voller Länge zu sehen. Abgesehen von der Sonne (unten rechts) sind jedoch alle anderen Himmelsobjekte zu klein, um dann noch entdeckt werden zu können.
Es folgt die Prozedur "draw_planets". Hier werden alle Himmelskörper in die aktuelle
"All-Blase" hinein gerendert.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
//Planeten----------------------------------------------
procedure thauptf.draw_planets;
var
abstand:double;
r,rd:integer;
planet:tobj;
begin
for r:=ord(_pluto) downto ord(_sonne) do begin
planet:=obja[r];
//Planet sichtbar?
abstand:=distance(px,py,pz,planet.x,planet.y,planet.z);
if(r<>ord(_sonne))and(abstand>_merkur_z-10000) then continue;
//auch Sonne weg bei genügend Abstand
if(abstand>2*_pluto_z) then continue;
//Zufallsterm für Gasplaneten: flimmern der Hülle
rd:=0;
if r=ord(_sonne) then rd:=random(6)
else if r=ord(_jupiter) then rd:=random(3)
else if r=ord(_saturn) then rd:=random(2)
else if r=ord(_uranus) then rd:=random(2)
else if r=ord(_neptun) then rd:=random(2);
if titelok and(abstand<100) then begin
glPushMatrix();
//springe zum planeten-ort
glTranslatef(planet.x,planet.y,planet.z);
glRotatef(getangle(10*rott),0,1,0);
glscalef(0.3,0.3,0.3);
glColor3f(0.5,0.5,0.5);
glPrint(planet.name);
glPopMatrix();
glColor3f(1,1,1);
end;
glPushMatrix();
//springe zum Planeten-Ort
glTranslatef(planet.x,planet.y,planet.z);
//Rotation, um Textur anzupassen
glRotatef(-rott,0,1,0);glRotatef(90,1,0,0);
//Textur und Sphere
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D,planet.tx);
gluSphere(planet.p,planet.r,trunc(20+rd),trunc(20+rd));
glDisable(GL_TEXTURE_2D);
//Staub, der um Paneten rotiert
draw_rotstaub(planet);
glPopMatrix();
glColor3f(1.0,1.0,1.0);
//'Attribute' der Planeten zeichnen ----------
if r=ord(_ceres) then draw_asteroids
else if r=ord(_saturn)then draw_saturnring
else if r=ord(_kuiper)then draw_komet;
end;
end;
Wir durchlaufen in einer Schleife den Index der Himmelsobjekte in umgekehrter
Reihenfolge. Zuerst wird Pluto ("_pluto") gemalt, dann sein Mond Charon, dann der
Kuipergürtel, dann Neptun usw. Bis wir schliesslich bei der Sonne ("_sonne")
angekommen sind.
Bei jedem Schleifendurchgang wird geprüft, ob es sich lohnt, das aktuelle Himmelsobjekt
zu rendern. Ist es zu weit vom Piloten entfernt, ist es nicht zu sehen, wir können uns
die Arbeit also sparen. Die "distance"-Funktion liefert uns die passenden Werte.
Die Sonne wird bei obiger Prüfung gesondert behandelt. Sie ist aus noch viel grösserer
Entfernung zu sehen als die anderen Planeten. Erst ab zweifachen Pluto-Abstand verschwindet
sie komplett aus unserem Sichtbereich.
Als Nächstes wird ein Radius-Delta "rd" bestimmt. Handelt es sich beim aktuellen
Objekt um die Sonne oder einen Gas-Planeten wie etwa Jupiter, dann bekommt "rd" einen
Zufallswert zugewiesen. Wozu, das sehen wir gleich.
Befindet sich der Pilot nahe am Objekt und ist der Titel-Modus aktiv, wird eine
rotierende 3D-Schrift gemalt, die den Namen des Himmelkörpers anzeigt.

3D-Titel im Planeteninneren: So manchen Himmelskörper erkennt der Nicht-Astronom erst, wenn er in dessen Inneres fliegt - sofern der Titel-Modus aktiv ist. Hier verrät uns der Titel beispielsweise, dass wir uns beim Mond Rhea befinden. Dann kann der Planet Saturn nicht mehr weit sein.
Der Zeichenstift wird (wieder) auf die Positionen des aktuellen Himmelobjekts
gebracht. Dann wird das Umfeld um "rott" Grad rotiert. Wir erinnern uns, "rott" ist
eine globale Variable, die in "takttTimer" jede 50stel-Sekunde um 0.5 Grad reduziert
wird. Ist sie kleiner als Null, wird sie auf 360 Grad hochgesetzt. Dadurch erhalten wir
eine permanente Rotation aller Himmelsobjekte um ihre eigene Achse.
Damit die Texturen besser passen, wird das Modell noch einmal
um 90 Grad gekippt. Mh ... effektiver wäre es ja gewesen, die Texturen vorher anzupassen
und sich diesen Schritt zu sparen. Hole ich beim nächsten Universum nach ...

Textur-Rotation nötig: Ohne Rotation um 90 Grad auf der y-Achse stimmen die Texturen nicht. Die Erde etwa würde sonst - wie hier gezeigt - um den Äquator rotieren, statt um die Pole.
Über "gluSphere" wird das Himmelsobjekt generiert. Dank des "rd"-Wertes, den wir eben
für die Gas-Planeten ermittelt haben, kann dabei der "Feinheitsgrad" der Kugel leicht
variieren, wodurch eine Art Flimmer-Effekt der Atmosphäre simuliert wird.
Es bietet sich an, nun auch gleich die "Attribute" des aktuellen Himmelskörpers
abzuarbeiten. Beim Saturn etwa müssen die Ringe nachgetragen werden. Exoten wie
Kometen und Asteroiden bedürfen eine Extra-Behandlung. Und der Rotationsstaub,
der alle grossen Himmelsobjekte umgibt, muss auch noch generiert werden.
Fangen wir mit dem Rotationsstaub an. Gemeint ist damit eine Masse von "Punkten",
die sich um die Himmelskörper bewegen. Im Gegensatz zum grauen "Normal"-Staub ist
der Rotationsstaub rötlich eingefärbt.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
//Rotationsstaub um Planeten----------------------------------
procedure thauptf.draw_rotstaub(planet:tobj);
var
d,abstand,
rot,mx,my,mz:double;
i,r:integer;
begin
//Rotationsstaub aktiv?
if rotstaubcsb.tag=0 then exit;
//Rotationsstaub um Planeten sichtbar?
abstand:=distance(px,py,pz,planet.x,planet.y,planet.z);
if abstand>3*_staub_dim then exit;
//Anzahl Staub nimmt ab, je weiter planet weg
i:=rotstaubcsb.tag-1;
d:=1;
if abstand>_staub_dim/2 then begin
d:=(abstand-_staub_dim/2)/100;
d:=(d*abstand)/(_staub_dim)+1;
end;
i:=trunc(i/d);
glpushmatrix();
//Staubrotation um fixen Wert, damit
//Planet- und Mondstaub nicht synchron laufen
rot:=trunc(planet.z) mod 360;
glRotatef(rot,1,1,1);
glpointsize(1);
glColor3f(1.0,0.8,0.5);
//berechnete Staubanzahl ausgeben
for r:=0 to i do begin
mx:=stauba[r].x-_staub_dim/2;
my:=stauba[r].y-_staub_dim/2;
mz:=stauba[r].z-_staub_dim/2;
glBegin(GL_POINTS);
glVertex3f(mx,my,mz);
glEnd();
end;
glpopmatrix();
end;
Zunächst wird geprüft, ob die Anzahl darzustellender Staubkörner, die im
"Tag"-Attribut der ScrollBar "rotstaubsb" des Cockpits steht, nicht auf null
gesetzt wurde. In diesem Fall geht es gleich wieder raus aus der Prozedur.
Dann wird geprüft, wie weit weg wir uns vom Zentrum des rotierenden Staubs
befinden. Sind wir zu weit weg, sparen wir uns die Malaktion.
Jetzt folgt eine Formel, die die maximale Anzahl der zu malenden Staubkörner aus
dem aktuellen Abstand zum Staubzentrum berechnet. Zweck der Übung ist, um so weniger
Staubkörner erscheinen zu lassen, je weiter wir uns von dem zentralen Himmelskörper
wegbewegen.
Idealerweise hätte man ja den Abstand zu jedem Staubkorn extra berechnet.
Denn durch die Rotation bewegen sich die Staubkörner ja unter Umständen auf
uns zu bzw. weg. Leider war ich jedoch nicht in der Lage, dazu eine ordentliche -
und vor allem schnelle - Funktion zu programmieren. So geht es aber auch.
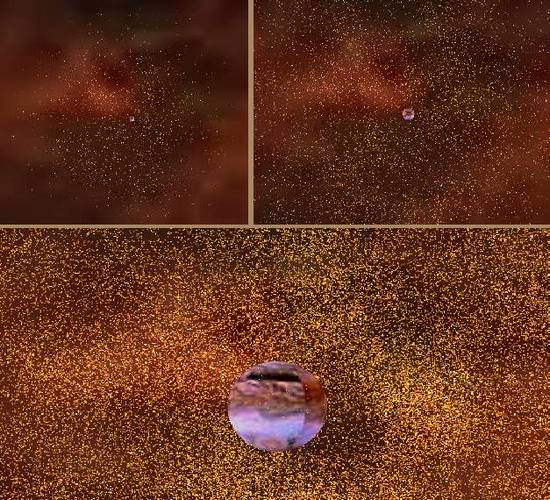
Dichtezunahme des Rotationsstaubs: Je näher wir an den Jupiter herankommen, umso mehr ist von seinem Rotationsstaub zu sehen - und dem seiner zahlreichen Monde. Bei voller Intensität sind Hunderttausende von Kleinstpartikel zu sehen, die von der Gravitation der grösseren Himmelskörper eingefangen wurden.
Da wir uns noch im "pushMatrix"-Block von "draw_planets" befinden und
dort bereits eine Rotation um die y-Achse vorgenommen haben, müssen
wir die Staubkörner eigentlich nicht noch einmal extra rotieren.
Wir berechnen allerdings trotzdem einen weiteren Rotationswert. Teilweise befinden
sich nämlich mehrere Himmelskörper in unmittelbarer Nähe (z.B. bei Planeten mit ihren
Monden). Bei exakt gleichem Rotationsgrad würden alle Rotationsstaubkörner synchron
laufen. Das aber sieht unschön aus.
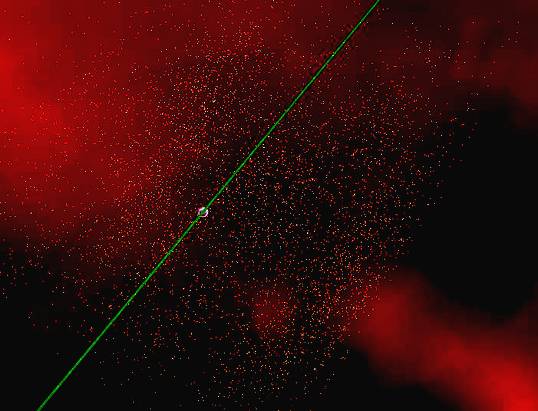
Unnatürlich synchronisierter Rotationsstaub: Synchron rotierende Staubkörner (hier von Jupiter und seinen Monden) mit verschiedenen, ein-achsig verschobenen Zentren bilden unnatürliche Linien. Daher variieren die Rotationsparameter, um solch unschöne Effekte zu vermeiden.
Gut, die Rotation hätten wir. Fehlen noch die Staubkörner an sich. Die zeichnen wir, indem
das Staub-Array "stauba" bis zum berechneten Maximum durchlaufen wird. Die Positionswerte
werden umgerechnet, sodass der aktuelle Planet den Mittelpunkt bildet. Ausgegeben werden
die Staubkörner letztlich über "glVertexf" als "dreidimensionale" Punkte.
Übrigens hat die Grösse eines Himmelobjekts in "OGL_Planets" keinen Einfluss auf die Dichte oder
Ausdehnung des Rotationsstaubs. Dem kleinsten Mond haftet genauso viel Dreck an wie der
Sonne. Da habe ich es mir einfach gemacht. Entsprechend verdoppelt sich die Staubmenge mit
jedem weiteren Himmelskörper. In Mond reichen Gebieten wie etwa dem Jupiter kommt somit
eine ganze Menge Unrat zusammen.
Addition von Rotationsstaub: Jeder grössere Himmelskörper in 'OpenGL Planets' bindet Rotationsstaub in gleicher Anzahl, also unabhängig von seiner Grösse. In Gebieten mit vielen Monden, wie etwa beim Jupiter, kommt da einiges an Staub zusammen.
Haben wir in "draw_planets" den Saturn gezeichnet, folgen nun seine Ringe. Ringstrukturen,
die bei anderen Planeten gefunden wurden, wie etwa dem Uranus (oder war es Neptun? Nein,
laut Wikipedia haben sogar Jupiter, Saturn, Uranus und Neptun Ringe ausgebildet),
werden in "OHL_Planets" dagegen nicht berücksichtigt.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
//--------------------------------------------------------------
procedure thauptf.draw_saturnring;
begin
glPushMatrix();
glTranslatef(obja[ord(_saturn)].x,obja[ord(_saturn)].y,obja[ord(_saturn)].z);
//Ring-Disk passend drehend
glRotatef(80,1.0,0,0);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D,obja[ord(_mond)].tx);
//innerer Ring
gluDisk(saturn_ring,_saturn_r+20,_saturn_r+50,18,8);
//äusserer Ring
gluDisk(saturn_ring,_saturn_r+60,_saturn_ring_r,18,8);
glDisable(GL_TEXTURE_2D);
glRotatef(-80,1.0,0,0);
glPopMatrix();
end;
Zur Generierung der Ringe werden zwei Quadric-Objekte vom Typ "gluDisks" verwendet,
eine für einen inneren und eine für einen äusseren Ring. In Wahrheit hat Saturn
natürlich viel, viel mehr Ringe, aber so genau müssen wir es ja nicht nehmen.
Eine weitere Vereinfachung ist, dass für die Ringe keine eigene Textur spendiert
wurde. Stattdessen verwenden wir die Textur des Erde-Mondes. Das spart Speicherplatz
und sieht dennoch passabel aus.
Ach ja, die Ringe wurden etwas um die y-Achse gekippt, sodass sie nicht ganz plan
sind mit der Planeten-Rotationsebene um die Sonne. Das sieht nicht nur besser aus,
sondern entspricht so in etwa auch der Realität.
Der modellierte Saturn: Der zweitgrösste Planet in unserem Solarsystem. Trotz einiger Hüftringe ein echter Hingucker, auch als Modell in 'OpenGL Planets'.
Zwischen Mars und Jupiter klafft eine Lücke, in der einst ein weiterer Planet seine
Bahnen zog, wie einige Wissenschaftler mutmassen. Ein Indiz dafür ist, das sich dort
zahlreiche Gesteinsbrocken finden lassen - die Asteroidenfelder. Womöglich sind diese
die letzten Überbleibsel jenes Planeten, der vor Urzeiten bei einer kosmischen Katastrophe
zerstört worden sein mag.
Nachdem in "draw_planets" Ceres gezeichnet wurde, folgen nun die restlichen Asteroiden.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
//--------------------------------------------------------------
procedure thauptf.draw_asteroids;
var
x,y,z:double;
vz,r:integer;
planet:tobj;
begin
planet:=obja[ord(_ceres)];
for r:=0 to _asteroid_c-1 do begin
glPushMatrix();
//asteroiden um ceres herum platzieren
x:=planet.x-_asteroid_dim/2+asteroida[r].x;
y:=planet.y-_asteroid_dim/2+asteroida[r].y;
z:=planet.z-_asteroid_dim/2+asteroida[r].z;
glTranslatef(x,y,z);
//Rotation, damit nicht alle Asteroiden identisch aussehen
vz:=1;if r mod 2=1 then vz:=-1;
glRotatef(getangle(vz*rott*((r mod 20)+1)+r),1,1,1);
//Textur und Sphere, weniger fein als bei den Planeten
//und in verschiedenen Grössen
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D,planet.tx);
gluSphere(planet.p,0.1*((r mod 20)+1),5,5);
glDisable(GL_TEXTURE_2D);
glPopMatrix();
end;
end;
Als Mittelpunkt des Asteroidenfeldes definieren wir die Position von Ceres.
Die Array-Werte von "asteroida" werden entsprechend umgerechnet.
Mh .., mir fällt gerade auf, dass die Umrechnung sinnvollerweise schon in
"initObjects" erledigt worden wäre. Nur einmal, statt bei jeder Malaktion neu.
Egal, das bleibt jetzt so.
Über einen Modulo-Wert wechseln wir die Rotationsrichtung einzelner Asteroiden.
Auch der Rotationsgrad bleibt nicht einheitlich. So drehen sich einige Brocken
schnell um die y-Achse, während andere sich langsam mehr um die x-Achse drehen.
Das bringt etwas Abwechslung hinein.
Die "gluSphere" bekommt mit dem Wert "5" einen geringeren "Feinheitsgrad" als
die Planeten. Dadurch gleichen die Asteroiden weniger exakten Kugeln, werden
eckiger, realistischer - und von OGL wohl auch schneller abgearbeitet.
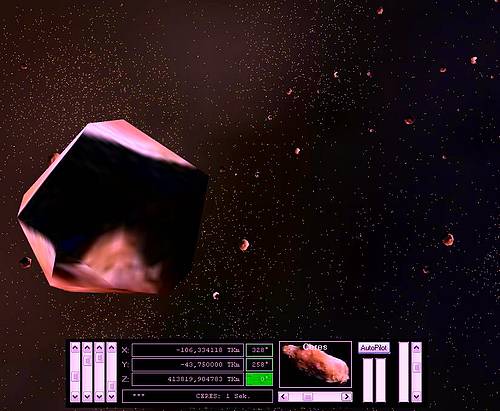
Mitten im Asteroidengürtel: Grobförmige, rotierende Brocken umschwirren unser Raumschiff. Da wünscht man sich fast eine Asteroiden brechende Bordkanone.
Jenseits von Neptun vermutet man zahlreiche weitere Himmelsobjekte, die aber einen Tick
zu klein sind, um noch von der Erde aus gesehen werden zu können. Pluto scheint dort nur
ein grösseres Objekt unter unzähligen weiteren Objekten zu sein. Weshalb der arme Kerl
ja erst kürzlich zum Zwergplaneten degradiert wurde.
In diesem sogenannten Kuipergürtel vermutet man auch den Ursprungsort vieler Kometen.
Diese "schmutzigen Schneebälle" stürzen immer wieder einmal ins Innere des Sonnensystems.
Partikel aus Staub und Eis lösen sich dann ab und bilden den charakteristischen Schweif.
Das sieht zu spektakulär aus, als dass wir es in "OHL_Planets" ignorieren könnten.
Wenigstens einen dieser uralten Gesellen lassen wir durch folgende Prozedur generieren:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
//--------------------------------------------------------------
procedure thauptf.draw_komet;
var
abstand,x,y,z,d:double;
r,anzahl:integer;
begin
glPushMatrix();
//zum kuiper-guertel sprungen
glTranslatef(obja[ord(_kuiper)].x,obja[ord(_kuiper)].y,obja[ord(_kuiper)].z);
//Eispartikel, blau gefärbt
glpointsize(3);
glColor3f(0.5,0.8,1.0);
//Schweif rotiert um z-Achse
glRotatef(rott,0,0,1);
//Kometenstaub nimmt ab mit Abstand zum Kometen
abstand:=distance(
px,py,pz,
obja[ord(_kuiper)].x,obja[ord(_kuiper)].y,obja[ord(_kuiper)].z
);
anzahl:=_staub_c-1;
d:=1;
if abstand>_staub_dim/200 then begin
d:=(abstand-_staub_dim/200);
d:=(d*abstand)/(_staub_dim)+1;
end;
anzahl:=trunc(anzahl/d);
//Grad der Auffächerung
d:=0.02/_staub_dim;
//hole Anzahl Eispartikel aus Staub-array
for r:=0 to anzahl do begin
//berechne Koordinaten so, dass der
//Kometen-Körper den Kopf bildet
x:=stauba[r].x-_staub_dim/2;
y:=stauba[r].y-_staub_dim/2;
z:=stauba[r].z-obja[ord(_kuiper)].r;
//lasse Staub in z-Achse fliessen
//wenn über den Schweif hinaus,
//dann wieder nach vorne holen
z:=(trunc(z)+taktc*(10))mod _staub_dim;
//fächere Schweif auf mit wachsendem z
x:=x*(0.001+(z*d));
y:=y*(0.001+(z*d));
//verdichte Partikel auf z-Achse
z:=z/5;
//gib Partikel aus
glBegin(GL_POINTS);
glVertex3f(x,y,z);
glEnd();
end;
glpointsize(1);
glPopMatrix();
end;
Zunächst positionieren wir den OGL-Malstift auf den Kuipergürtel,
so auf halber Strecke zwischen Neptun und Pluto. Wir setzen die Stiftbreite auf "3" Pixel
und ändern die Farbe in Blau. Damit malen wir gleich den Partikelstrom, der aus
dem Kometen "fliesst".

Kometenschweif: Ein Strom von Eiskristallen bricht aus dem Kometen heraus und bilden den charakteristischen Schweif. Dieser ist im Schnitt ca. 100 km lang, kann aber auch eine Ausdehnung von mehreren Millionen km haben. Der Schweif weist dabei nicht in Bewegungsrichtung des Kometen, sondern immer von der Sonne weg.
Wir benutzen die globale Variable "rott", um den Partikelstrom fortlaufend um
die z-Achse rotieren zu lassen.
Ähnlich wie beim Rotationsstaub berechnen wir einen Maximalwert "anzahl" für das
Array "stauba", der mit steigendem Abstand zum Kometen abnimmt.
Zusätzlich wird der Auffächerungsgrad "d". Dieser Wert dient dazu, den Schweif
des Kometen mit zunehmenden Abstand immer breiter werden zu lassen.
Nun durchlaufen wir das Staub-Array "stauba" von "0" bis "anzahl". Die Koordinaten
im Array werden auf die Positionen des Kometen umgerechnet. Null-Werte der z-Achse
entsprechen der Entfernung des Kometen zur Sonne. Dadurch landen grösseren Werte
automatisch hinter dem Kometen, weiter weg von der Sonne, was so ja auch den
natürlichen Gepflogenheiten von Kometenschweifen entspricht.
Um nun Bewegung in die Sache zu bekommen - ausser der Schweif-Rotation, die OGL für
uns berechnet -, benutzen wir den globalen Taktzähler "taktc", um die z-Achsenwerte
des Staub-Arrays zu inkrementieren. Bei jedem "Taktschlag" rücken so die Partikel
weiter vom Kometen ab. Gleichzeitig nutzen wir unser "d", um die x- und y-Werte
der Partikel durch Multiplikation mit dem z-Achsenwert zunehmend zu vergrössern, wodurch
der Schweif nach hinten hin immer breiter wird.

Auffächerung des Kometenschweifs: Der Grad der Auffächerung eines Kometenschweifs lässt sich in 'OpenGL Planets' vorgeben. Je grösser dieser Wert wird umso breiter wird der Schweif dargestellt (Bild unten).
Durch die Modulo-Division bei der Berechnung des z-Achsenwertes sorgen wir dafür, dass uns
das Material nicht ausgeht. Jeder z-Achsenwert des Staub-Arrays wandert dadurch immer wieder
von seinem Ursprungswert bis auf ein Maximum ("staubdim"), springt dann auf null um,
wächst wiederum bis zum Ursprungswert an und weiter bis zu Maximum - und wiederholt
dann das Ganze von vorne.
Mathematik ist mit Worten schwer zu beschreiben. Zumal ich hinterher oft selbst nicht
weiss, was ich da so treibe. Es wird experimentiert, bis es passt. Am Kometenschweif,
so wie er jetzt ist - und der wahrlich verbesserungswürdig wäre -, habe ich bestimmt
ein bis zwei Stunden gesessen.

Komet in 'OpenGL Planets': Der Schwammsche Komet - ein einsames Leuchtfeuer am Rande des Solarsystems von 'OpenGL Planets'. In dieser Entfernung zur Sonne bildet sich übrigens in Wirklichkeit bei einem Kometen noch kein Schweif aus. Diese werden erst ab der Marsbahn sichtbar, denn ab jener ist der Sonnenwind intensiv genug wird, um Eispartikel aus dem Kern lösen zu können.

Komet in der Realität: Der Halleysche Komet 1986 im Teleskop. Er ist ein sogenannter kurzperiodischer Komet, der von der Erde aus alle 75-77 Jahre zu beobachten ist. Die zeitlichen Abweichungen verdanken wir hauptsächlich Jupiter, dessen gewaltige Gravitationswirkung die Bahn von Halley beeinflusst. Quelle: NASA/JPL.
Die Prozedur "draw_planets" haben wir abgearbeitet. Wir kehren zu "draw_scene" zurück.
Dort ist jetzt "draw_staub" an der Reihe:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
//Staub----------------------------------------------
procedure thauptf.draw_staub;
procedure set_xyz(p_xyz,mm_xyz,md_xyz:double;var m_xyz:double);
begin
if m_xyz=0 then exit;
if p_xyz<0 then begin
if m_xyz<Abs(mm_xyz) then
m_xyz:=(md_xyz-1)*_staub_dim-m_xyz
else
m_xyz:=(md_xyz-0)*_staub_dim-m_xyz;
m_xyz:=m_xyz+(_staub_dim div 2);
end
else begin
if m_xyz<mm_xyz then
m_xyz:=(md_xyz+1)*_staub_dim+m_xyz
else
m_xyz:=(md_xyz+0)*_staub_dim+m_xyz;
m_xyz:=m_xyz-(_staub_dim div 2);
end;
end;
var
mmx,mmy,mmz,
mdx,mdy,mdz,
mx,my,mz:double;
r:integer;
begin
if staubcsb.tag=0 then exit;
glPushMatrix();
glColor3f(0.8,0.8,0.4);
glpointsize(1);
mmx:=(trunc(px) mod _staub_dim);
mmy:=(trunc(py) mod _staub_dim);
mmz:=(trunc(pz) mod _staub_dim);
mdx:=(trunc(px) div _staub_dim);
mdy:=(trunc(py) div _staub_dim);
mdz:=(trunc(pz) div _staub_dim);
for r:=0 to staubcsb.tag-1 do begin
mx:=stauba[r].x;set_xyz(px,mmx,mdx,mx);
my:=stauba[r].y;set_xyz(py,mmy,mdy,my);
mz:=stauba[r].z;set_xyz(pz,mmz,mdz,mz);
glBegin(GL_POINTS);
glVertex3f(mx,my,mz);
glEnd();
end;
glPopMatrix();
end;
Raum-Staub, der überall im Modell auftauchen soll, ist schwerer zu realisieren,
als man vermuten sollte.
Der erste Versuch ging daneben: nämlich die Anlage eines grossen Arrays, bestehend
aus exakt einer Million Punkt-Koordinaten, die sich über den kompletten Raum der
"All-Blase" verteilten.
Diese Millionen Punkte, das klingt erst einmal nicht wenig. Doch einmal mehr wurde
deutlich, wie gross das Solarsystem ist. Denn praktisch kein Staubkorn war weit und
breit zu sehen. Sie gingen in den Weiten des virtuellen Alls einfach völlig unter.
Genauso gut hätte ich auch nur 10 Punkte verteilen können.
Mir kam die naheliegende Idee, einen kleineren Raum mit Staubkörnern abzudecken,
diesen Raum aber quasi mit mir mit zu schleppen, während ich mich durch die "All-Blase"
bewege. Genauer: Der Raum-Staub befindet sich in einem Quader von "_staub_dim" (5000) Tkm.
Der Pilot hockt in der Mitte. In alle Richtungen hat es also ordentlich Staub. Nun bewegt
man sich auf der z-Achse tiefer in den Raum hinein. Um die Bewegung zu simulieren, müssen
die Koordinaten-Punkte des Staub-Arrays folgerichtig um den gleichen Wert nach "vorne",
also aus dem Bildschirm heraus, verschoben werden.
Es war klar, dass man so früher oder später die Grenze des
Arrays erreicht hätte und einem dann die Staubkörner "vor einem" ausgehen würden.
Deshalb musste dafür gesorgt werden, dass die "aus dem Bildschirm gefallenen"
Staubkörner auf der anderen Seite, sprich, vor einem, wieder auftauchen würden.
Typischer Fall für einen von der Piloten-Position abhängigen Modulo-Wert, der
irgendwie auf die Koordinaten-Werte der Staubkörner aufzurechnen war.
Mein lieber Schwan hatte es dieses "irgendwie" in sich! Es kostete mich nämlich
zwei Tage, drei Schachteln Zigaretten, eine Kanne Kaffee und bestimmt ein paar
Millionen geplatzter Neuronen, bis ich es in funktionierenden Quellcode umgesetzt
hatte. Und ich lernte auf die harte Tour: Unterschätze nie ein "irgendwie"!
Als mir dann - mit obiger Prozedur - der Raum-Staub erstmals in unendlicher Wiederholung
wie geplant um die Ohren flog, in jeder Richtung, egal wo, egal wie lange, war es, als
hätte ich höchstselbst die Antigravitationsformel geknackt.
Eine Erklärung gibt es nicht. Denn ich weiss nicht mehr, warum das Ding funktioniert.
Es tut es jedenfalls. Und ich werde kein verdammtes Byte mehr daran ändern. Punkt.

Wie 'berechnet' man Staub im All? Auf dem Weg zur Staubformel. Letzte Reste einer qualvollen Annäherung. Nur echt mit Schweiss- und Kaffeeflecken ...
Angesicht der riesigen Entfernungen im Solarsystem gibt es auch in "OGL_Planets" den aus
der SciFi-Literatur propagierten Königsweg des Hyperraumes, um Distanzen schneller hinter
sich bringen zu können.
Nicht dass es wichtig wäre, aber dennoch: Man kann sich den
Hyperraum als einen mit Tachyonen angefüllten Raum denken. Diese Teilchen bewegen
sich permanent mit Überlichtgeschwindigkeit und können nur mit unendlichem
Energieaufwand auf Lichtgeschwindigkeit abgebremst werden. Transferiert in Tachyonen
rast man mit aberwitziger Geschwindigkeit durch den Raum und materialisiert sich am
Zielort wieder.
Eine weitere Vorstellung ist die, dass sich im Hyperraum ein Schwarzes Loch befindet.
In dessem Zentrum gelten die physikalischen Gesetze der "normalen" Welt nicht mehr.
Singularitätszustand. Division by Zero. Hier ist im Prinzip alles möglich: unendliche
Materiebildung aus dem Vakuum ebenso wie unendliche Geschwindigkeit.
Eine dritte Variante stellt sich den Hyperraum als von einem Wurmloch gebildet vor. Das
vermag die vierdimensionale Raumzeit derart zu krümmen, dass ein Körper darin nicht über
die Oberfläche der ins Dreidimensionale übertragenen Raum-Zeit-Kugel wandern muss, um auf
die andere Seite zu kommen, sondern den kürzeren Weg nehmen kann, nämlich "mitten
hindurch".
Wie dem auch sei, unser Hyperraum zumindest wird mit Bits und Bytes realisiert:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
//HyperMove-Tunnel--------------------------------------
procedure thauptf.draw_hypermove;
const
_TEXTURE_SPEED=1/20;
var
i,j:integer;
angle,j1,j2:glFLoat;
begin
//HyperMove aktiv?
if taktt.tag<>_ap_hmflug then exit;
glPushMatrix();
gldisable(GL_DEPTH_TEST);
glTranslatef(px,py,pz);
glRotatef(roty-ap_spotx,0,1.0,0);
glRotatef(rotz,0,0,1);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D,hypermove_tx);
glLineWidth(1);
angle:=taktc;
glColor3f(1,1,1);
for j:=0 to _hypermove_len-1 do begin
j1:=(j )/12+angle*_TEXTURE_SPEED;
j2:=(j+1)/12+angle*_TEXTURE_SPEED;
glBegin(GL_QUADS);
For i:=0 to 11 do begin
glTexCoord2f((i-3)/12,j1);
glVertex3f(hypermove[i, j ].X,hypermove[i, j ].Y,hypermove[i, j ].Z);
glTexCoord2f((i-2)/12,j1);
glVertex3f(hypermove[i+1,j ].X,hypermove[i+1,j ].Y,hypermove[i+1,j ].Z);
glTexCoord2f((i-2)/12,j2);
glVertex3f(hypermove[i+1,j+1].X,hypermove[i+1,j+1].Y,hypermove[i+1,j+1].Z);
glTexCoord2f((i-3)/12,j2);
glVertex3f(hypermove[i, j+1].X,hypermove[i, j+1].Y,hypermove[i, j+1].Z);
end;
glEnd();
end;
glDisable(GL_TEXTURE_2D);
glLineWidth(1);
glenable(GL_DEPTH_TEST);
glPopMatrix();
end;
Wir stellen zunächst fest, ob wir uns im Hyper-Move-Modus befinden. Ist dem nicht so,
geht es gleich wieder raus aus der Prozedur.
Wir schieben und drehen das Röhren-Ende so zurecht, dass es etwa in der Mitte
des Bildschirms erscheint. Geringfügige Abweichungen nach links und rechts sind möglich,
abhängig von der Position des "Spots" (siehe Abschnitt "Spielen mit dem Hyper-Move-Spot").
Dann wird der Tunnel, dessen "Eckpunkte" zuvor in einem zweidimensionalen Array
eingetragen wurden, der Länge nach durchlaufen. Der Wert von "angle" wird mit jedem
"Taktschlag" des Universums erhöht und fliesst - mit "_TEXTUR_SPEED" multipliziert - in
die Koordinaten-Werte "j1" und "j2" der HyperMove-Textur ein.
In einer inneren Schleife werden die 12 Randpunkte des jeweiligen Längenabschnitts
über "glVertex2f" gesetzt. Darauf wird jeweils ein Stück Textur "geklebt", welches
jedoch über die eben berechneten "j1"- und "j2"-Werte verschoben erscheint. Die
Textur wandert so fortlaufend am Rande des Tunnels auf den Betrachter zu, was den
Eindruck einer rasenden Fahrt mitten hindurch vermittelt.

HyperMove-Textur: In diesem alternativen HyperMove-Tunnel für Vampirjäger kommt uns gerade das hübsche Gesicht von Buffy näher und näher und näher, indem die zugehörige Textur entlang des Tunnels verschoben wird. Buffy the Vampire Slider gewissermassen ...
Das All wurde gezeichnet, ebenso alle Planeten nebst Attributen, der Raum-Staub ist
verteilt, der Hyper-Move-Tunnel abgearbeitet. Fehlt noch ein Fadenkreuz, welches
einem den Zielpunkt markiert, auf den gerade zugeflogen wird. Diesen Job übernehmen
folgende Prozeduren:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
00071
00072
00073
00074
00075
00076
00077
00078
00079
00080
00081
00082
00083
00084
00085
00086
00087
00088
//Fadenkreuz-------------------------------------------------------
procedure thauptf.draw_fadenkreuz;
var
rd:integer;
begin
glColor3f(1.0,1.0,1.0);
if(taktt.tag=_ap_stop)and not visierok then exit;
glPushMatrix();
gldisable(GL_DEPTH_TEST);
glLoadIdentity;
glTranslatef(0,0,-20);
glLineWidth(2);
rd:=3;
if(taktt.tag=_ap_hmstart)or(taktt.tag=_ap_hmflug)then begin
//Rahmen instabil
glColor3f(1,0.5,0.0);
glBegin(GL_LINE_LOOP);
glVertex3f( rd, rd, -rd*3);
glVertex3f(-rd, rd, -rd*3);
glVertex3f(-rd,-rd, -rd*3);
glVertex3f( rd,-rd, -rd*3);
glEnd();
//Rahmen stabil
glColor3f(0.0,1.0,0.0);
glBegin(GL_LINE_LOOP);
glVertex3f( rd, rd, -rd*15);
glVertex3f(-rd, rd, -rd*15);
glVertex3f(-rd,-rd, -rd*15);
glVertex3f( rd,-rd, -rd*15);
glEnd();
end;
//Kreuz
glColor3f(1.0,1.0,1.0);
glLineWidth(1);
glBegin(GL_LINES);
glVertex3f(-rd,-rd,rd);glVertex3f(rd,rd,rd);
glVertex3f(rd,-rd,rd);glVertex3f(-rd,rd,rd);
glEnd();
//Rahmen
glLineWidth(2);
if taktt.tag=_ap_hmflug then glColor3f(1.0,0.0,0.0)
else glColor3f(1.0,1.0,1.0);
glBegin(GL_LINE_LOOP);
glVertex3f( rd, rd, rd);
glVertex3f(-rd, rd, rd);
glVertex3f(-rd,-rd, rd);
glVertex3f( rd,-rd, rd);
glEnd();
draw_spot;
glLineWidth(1);
glenable(GL_DEPTH_TEST);
glPopMatrix();
end;
//Spot-----------------------------------------
procedure thauptf.draw_spot;
var
rd:integer;
begin
if(taktt.tag<>_ap_hmstart)and(taktt.tag<>_ap_hmflug)then exit;
glPushMatrix();
gldisable(GL_DEPTH_TEST);
glLoadIdentity;
glRotatef(rotz,0.0,0,1);
glTranslatef(ap_spotx,0,-20);
glLineWidth(2);
rd:=3;
glScalef(0.1,0.1,0.1);
glColor3f(1.0,1.0,1.0);
glBegin(GL_LINE_LOOP);
glVertex3f( rd, rd, -rd);
glVertex3f(-rd, rd, -rd);
glVertex3f(-rd,-rd, -rd);
glVertex3f( rd,-rd, -rd);
glEnd();
glLineWidth(1);
glenable(GL_DEPTH_TEST);
glPopMatrix();
end;
Wurde das Visier deaktiviert und befinden wir uns nicht im Autopilot-Modus,
gibt es nichts weiter zu tun und wir verlassen die Prozedur.
Ansonsten schalten wir den Tiefentest aus, damit unser Visier nicht von sich
nähernden Objekten verdeckt wird, und transferieren den OGL-Zeichenstift 20 Tkm
vor uns.
Während der Hyper-Move-Phase werden zwei Rechtecke gezeichnet. Einmal ein kleiner
grüner Rahmen (der "grüne Bereich"), und einmal ein etwas grösseres Rechteck,
rötlich gefärbt, welches die Grenzen vorgibt, die der "Spot" nicht überschreiten
darf (der "kritische Bereich").
Anschliessend wird - egal, ob Hyper-Move aktiv ist oder nicht - über den Bildschirm ein
weisses Kreuz gelegt, welches die Bildschirmmitte schneidet. Eingerahmt wird das Ganze
durch ein weiteres Rechteck.

Visier im Cockpit: In unserem Raumschiff zeigt uns ein Visier mit Fadenkreuz an, in welche Richtung wir aktuell fliegen. Hier zum Beispiel haben wir gerade einen Kometen exakt aufs Korn genommen.
Zuletzt wird "draw_spot" aufgerufen, der Tiefentest wieder aktiviert und die Prozedur
verlassen.
In "draw_spot" wird jener kleine "Ball" gemalt, den der Pilot in der Mitte halten muss,
solange der Hyper-Move-Modus aktiv ist.
Die Position des "Spots" wird dabei zum einen vorgegeben durch den Rotationsgrad um
die z-Achse, "rotz", zum anderen durch die in "takttTimer" ständig neu ermittelte
Links-rechts-Abweichung "ap_spotx".
Geschafft! Unser Solarsystem wird dargestellt. Wir können uns darin bewegen. Der
Bordcomputer zeigt uns ständig, wo wir uns befinden oder wie lange die Reise zu
einem anvisierten Ziel bei aktueller Höchstgeschwindigkeit dauern würde. Die
Umgebung lässt sich in ihrem Aussehen variieren. Bildschirm-Elemente können an-
und ausgeschaltet werden.
Was uns jetzt noch fehlt, ist ein wenig Unterstützung für den Piloten, damit er die
gewünschten Himmelskörper leichter finden kann. Obwohl ja die "OGL_Planets"-Körper
im Gegensatz zur Realität nicht in festen Bahnen um die Sonne kreisen, sondern völlig
stillstehen (mal abgesehen von ihrer Eigenrotation).
Im Prinzip muss man nur dem Leitstrahl folgen, dann findet man früher oder später
jedes gesuchte Objekt. Meistens aber eher später. Denn - ich erwähnte es bereits ein-,
zweimal - die Dimensionen im Sonnensystem sind gewaltig. Ergo wird man bevorzugt die
maximale Höchstgeschwindigkeit wählen. Das wiederum hat aber zur Folge, dass man leicht
über das Ziel hinaus schiesst. Steuert man etwa von der Sonne aus mit Lichtgeschwindigkeit
auf die Erde zu, ist diese nach über 8 Minuten Dauerflug nur für einige wenige Sekunden
zu sehen, bevor wir sie durchquert und sofort wieder weit hinter uns gelassen haben.
Ein Autopilot musste also her, jemanden, der die Navigation für uns übernimmt. Und damit
die Fliegerei schneller geht, kann man zusätzlich den Weg über den Hyperraum nehmen,
sofern die Strecke nur gross genug ist.
Ein Klick auf den Button "apb" aktiviert den Autopiloten. Er bringt uns zu dem Ziel,
welches im Monitor des Cockpits ausgewählt wurde. Beliebige Koordinatenpunkte können
hier dagegen nicht angegeben werden.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
procedure Thauptf.apbClick(Sender: TObject);
begin
if apb.Caption='STOPP' then begin
ap_steps:=_ap_break_steps;
taktt.tag:=_ap_break;
activecontrol:=nil;
end
else begin
apb.Caption:='STOPP';
activecontrol:=nil;
cockpitp.Color:=clred;
ap_spotx:=0;
ap_err:=0;
ap_z:=_sonne_z;
case zielsb.position of
ord(_sonne) :ap_z:=_sonne_z;
ord(_merkur):ap_z:=_merkur_z;
ord(_venus) :ap_z:=_venus_z;
ord(_mond) :ap_z:=_mond_z;
ord(_erde) :ap_z:=_erde_z;
ord(_deimos):ap_z:=_deimos_z;
ord(_phobos):ap_z:=_phobos_z;
ord(_mars) :ap_z:=_mars_z;
ord(_ceres):ap_z:=_ceres_z;
ord(_kallisto):ap_z:=_kallisto_z;
ord(_ganymed) :ap_z:=_ganymed_z;
ord(_europa) :ap_z:=_europa_z;
ord(_io) :ap_z:=_io_z;
ord(_jupiter) :ap_z:=_jupiter_z;
ord(_titan) :ap_z:=_titan_z;
ord(_rhea) :ap_z:=_rhea_z;
ord(_saturn):ap_z:=_saturn_z;
ord(_oberon) :ap_z:=_oberon_z;
ord(_titania):ap_z:=_titania_z;
ord(_uranus) :ap_z:=_uranus_z;
ord(_triton):ap_z:=_triton_z;
ord(_neptun):ap_z:=_neptun_z;
ord(_kuiper):ap_z:=_kuiper_z;
ord(_charon):ap_z:=_charon_z;
ord(_pluto) :ap_z:=_pluto_z;
end;
//Direktflug oder Hyper-Move?
if distance(
px,py,pz,
obja[zielsb.position].x,obja[zielsb.position].y,obja[zielsb.position].z
)<=_ap_direkt_distance
then ap_gpb.max:=2 //Direktflug: ap_richtung, ab_direkt
else ap_gpb.max:=4; //Hyper-Move : ap_richtung, b_hmstart, ap_hmflug, ap_hmbremsen
ap_gpb.Position:=ap_gpb.max;
//aktiviere Richtungsbestimmung
ap_steps:=_ap_richtung_steps;
taktt.tag:=_ap_richtung;
end;
end;
Zunächst prüfen wir anhand der Knopfbeschriftung, ob wir uns bereits im Autopilot-Modus
befinden. Ist dies der Fall, beenden wir diesen, indem das "taktt"-Tag auf "_ap_break"
gesetzt wird. Dadurch wird ab dem nächsten Taktschlag in "takttTimer" die Abbruchsphase
eingeleitet.
Ansonsten ermitteln wir, wie weit das Ziel entfernt ist ("ap_z"). Das lässt sich über die
Konstanten der z-Achsen-Werte der Himmelskörper erfahren, von dem wir später unsere eigene
z-Position abziehen (bzw. aufaddieren). Die Position der Cockpit-ScrollBar "zielsb",
des Ziel-Monitors, gibt uns dabei den Index des Planeten vor, den wir erreichen wollen.
Anschliessen wird entschieden, ob das Ziel nah genug für einen Direktflug ist oder
doch ein Hyperraum-Flug nötig ist. Die Werte liefert uns die bereits bekannte
Distanz-Funktion. Ein Direktflug per Autopilot lässt sich in zwei Phasen unterteilen,
ein Hyper-Move-Flug benötigt dagegen deren vier Phasen. Festgehalten wird dies in
der Variablen "ap_gpb.max".
Ganz am Schluss setzen wir noch das "taktt"-Tag auf "_ap_richtung". Dies bewirkt, dass
beim nächsten Aufruf von "takttTimer" die Richtungsphasen-Prozedur des Autopiloten
abgearbeitet wird.
Darauf bin ich nun wirklich stolz. Kraft meiner Gedanken habe ich es geschafft, einem
Computer die Fähigkeit zu geben, ein Raumschiff so auszurichten, dass es, wo immer es
sich im Raum auch befinden mag, mit der Spitze exakt auf ein Ziel weist, und sei dies
auch eventuell Millionen von Kilometern entfernt!
Geholfen hat wiederum Pythagoras. Denn neben der allgemein bekannten Formel zur
Berechnung der Länge der Hypotenuse "c" eines rechtwinkligen Dreiecks bei gegebener
Länge zweier Seiten "a" und "b" ...
|
c2 = a2 + b2
|
Rechtwinkliges Dreieck: Die Länge der Hypotenuse 'c' lässt sich über die Länge von 'a' und 'b' mithilfe des Satzes von Pythagoras ermitteln. Quelle: Wikipedia.
|
... gibt es auch eine erweiterte Form derselben Formel, den "Kosinussatz",
der für beliebige Dreiecke gilt - und in den insbesondere auch die inneren
Winkel des Dreiecks einfliessen:
|
c2 = a2 + b2 - 2ab cos(g)
|

Kosinusatz: Der Kosinussatz ist die Verallgemeinerung des Satzes von Pythagoras für nicht rechtwinklige Dreiecke. Quelle: Wikipedia.
|
Prima Sache. Denn kippen wir das Dreieck so zurecht, dass es für unseren Fall gilt, und lösen
nach Gamma auf, ergibt sich:
c2 = a2 + b2 - 2ab cos(g)
2ab cos(g) = a2 + b2 - c2
cos(g) = (a2 + b2 - c2) / (2ab)
g = arccos( (a2 + b2 - c2) / (2ab) )
|
Anwendung des Kosinussatzes: Mithilfe des Kosinussatzes können wir die Flugrichtung berechnen, um von einem beliebigen Ort aus ein beliebiges Ziel im Raum ansteuern zu können, sofern wir nur über die nötigen Koordinatenangaben verfügen.
|
Damit hätten wir alles, was wir brauchen. Gamma ist der gesuchte Winkel. Die Länge der
Strecke "a" ergibt sich aus dem Abstand des Piloten zur Sonne. Die Länge "b" aus dem
Abstand des Piloten zum Ziel. Und die Länge "c" ist die ebenfalls bekannte Strecke
Sonne zum Ziel.
Der berechnete Winkel muss um die Eigenrotation des Raumschiffs um die y-Achse
korrigiert werden. So ergibt sich jenes Winkel-Delta, das zur vorliegenden Ausrichtung
des Raumschiffs fehlt, um exakt den Zielpunkt anzuvisieren.
Ha! Mein Mathematik-Grundstudium hat sich also doch gelohnt. Obwohl ich zugeben muss,
dass mir noch nie zuvor der Arcuskosinus über den Weg gelaufen ist. Meines Wissen nach
benutze ich den hier zum ersten Mal in meinem Leben.
Hier nun den der Source zur Ausrichtung des Raumschiffs in Delphi:
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
00071
00072
00073
00074
00075
00076
00077
00078
00079
00080
00081
00082
00083
00084
00085
00086
00087
00088
00089
00090
00091
00092
00093
00094
00095
00096
00097
00098
00099
00100
00101
00102
00103
00104
00105
00106
00107
00108
00109
00110
00111
00112
00113
00114
00115
00116
00117
00118
00119
00120
00121
00122
00123
00124
00125
00126
00127
00128
00129
00130
00131
00132
00133
00134
00135
00136
00137
00138
00139
00140
00141
//Berechnung des Wertes für die lineare Beschleunigen/Abbremsung
//liefert Werte zwischen 0 und 1 zurück
//0 bei x=min, 1 bei x=Hälfte, 0 bei x=max
function thauptf.aufab_linear(xmin,x,xmax:double):double;
var
len:double;
begin
//len: 0 - 0.5 - 0
len:=xmax-xmin;len:=x/len;if len>0.5 then len:=1-len;
//len: 0 0,02 0,04 0,06 0,08 ... 1 ... 0,02 0
result:=2*len;
end;
//Autopilot: automatische Ausrichtung auf das Ziel -------------
procedure thauptf.ap_richtung;
{
* zx/zy
|\
| \
| \
a | \ c
| \
| \
| alpha\
|-------------*x/y
| b |
| |
| |
----*---------------------->
0/0
a^2 = b^2 + c^2 - 2*b*c*cos(alpha)
==>
b^2 + c^2 - a^2
alpha = arccos( --------------- )
2*b*c
}
function diffdeg2target(x,y,zx,zy,rot:double):double;
var
a,b,c:double;
alpha,diffw:double;
begin
a:=abs(zy-y);
b:=abs(zx-x);
c:=sqrt(a*a+b*b);
alpha:=degtorad(180-90)-arccos((b*b+c*c-a*a)/(2*b*c));
rot:=degtorad(rot);
if y>=zy then begin
//davor
if x<=zx then diffw:=alpha+rot //davor rechts
else diffw:=rot-alpha; //davor links
end
else begin
//dahinter
if x<=zx then diffw:=degtorad(180)+rot-alpha //dahinter recht
else diffw:=degtorad(180)+rot+alpha; //dahinter links
end;
diffw:=-radtodeg(diffw);
diffw:=getangle(diffw);
result:=diffw/ap_steps;
end;
procedure calcwinkel;
var
zx,zz:double;
begin
zx:=obja[zielsb.position].x;
zz:=obja[zielsb.position].z;
ap_dx:=0;
ap_dy:=0;
ap_dz:=0;
ap_dy:=diffdeg2target(px,pz,zx,zz,roty);
if rotx>=180 then ap_dx:=(360-rotx)/ap_steps
else ap_dx:=-rotx/ap_steps;
if rotz>=180 then ap_dz:=(360-rotz)/ap_steps
else ap_dz:=-rotz/ap_steps;
end;
var
d:double;
begin
//start
if ap_steps=_ap_richtung_steps then begin
//berechne Winkel zum Ziel
calcwinkel;
//y-Änderung ergibt sich aus Flugschritten
ap_mark_y:=py/ap_steps;
//Turbinen an
dosound(_snd_start,true);
end;
//Ende erreicht?
if
(ap_steps<=0)or
(abs(ap_dx+ap_dy+ap_dz)=0)
then begin
ap_gpb.Position:=ap_gpb.Position-1;
//Direktflug möglich?
if ap_gpb.max=2 then begin
//aktiviere Direktflug
ap_steps:=_ap_direkt_steps;
taktt.Tag:=_ap_direkt;
end
else begin
//aktiviere Hyper-Move
ap_steps:=_ap_hmstart_steps;
taktt.Tag:=_ap_hmstart;
end;
ap_spotx:=0;
exit;
end;
//linear beschleunigt/abgebremst Richtung fixieren
d:=aufab_linear(0,_ap_richtung_steps-ap_steps,_ap_richtung_steps);d:=d*2;
//mittlere Geschwindigkeit erreicht?
if d>1 then dosound(_snd_slow,true);
//abbremsen?
if(d<1)and(ap_steps<_ap_richtung_steps div 2) then dosound(_snd_bremsen,true);
rotx:=getangle(rotx+d*ap_dx);
roty:=getangle(roty+d*ap_dy);
rotz:=getangle(rotz+d*ap_dz);
//gleichzeitige Anpassung der Höehe
py:=py-d*ap_mark_y;
dec(ap_steps);ap_pb.Position:=ap_steps;
end;
Okay, die Prozedur "ap_richtung" wird jede 50-tel Sekunde aufgerufen, und zwar durch
unseren Universums-Takt "takttTimer". Die globale Variable "ap_steps" wird dabei
jedes Mal um eins dekrementiert, so lange, bis sie null ist. Das ist nach
"_ap_richtung_steps" Schritten der Fall.
Am Anfang wird geprüft, ob dies der erste Aufruf der Funktion ist. Wenn ja, dann
lassen wir die interne Funktion "calcwinkel" die Winkel-Änderungen um alle Achsen
berechnen, die nötig sind, damit das Raumschiff am Ende auf das Ziel ausgerichtet
ist.
Am schwierigsten ist das Winkel-Delta um die y-Achse zu berechnen. Die Theorie dazu
ist oben ja bereits beschrieben worden.
Mh ... ich merke gerade, dass ich mich nicht so ganz an diese Theorie gehalten habe.
Wie man in "diffdeg2target" erkennt, wird die Arcuskosinus-Formel um einen Zusatz-Term
korrigiert ... Und was übergebe ich denn da eigentlich für komische Längenwerte?
Tja, offenbar habe ich die Längenwerte auf ein rechtwinkliges
Dreieck übertragen. Und dann Gamma berechnet? Das haut seltsamerweise hin. Die Winkelsumme
im Dreieck hat 180 Grad, im rechtwinkligen Dreieck hat es einmal 90 Grad und der Rest
ergibt sich aus ... Ach, was weiss ich? Das Ganze scheint mir von mir unnötig
verkompliziert worden zu sein. Aber es funktioniert. Wir erhalten am Schluss das
gesuchte Gamma-Delta "ap_dy". 1.000 Flüge können sich nicht irren. Belassen wir es
also dabei.
Wesentlich einfacher funktioniert die Winkel-Delta-Berechnung bei den Rotationswinkeln
um die x- und z-Achse, denn die müssen in "_ap_richtung_steps" Schritten einfach nur
auf null gebracht werden. Eine simple Division erledigt den Job.
Wieder zurück in der Hauptprozedur wird als Nächstes geprüft, ob das Ende-Kriterium
für die "ap_richtung"-Funktion erfüllt ist. Wenn ja, dann wird die nächste Autopilot-Phase
eingerichtet, entweder einen Direktflug oder einen Hyper-Move-Sprung.
Ansonsten nutzen wir "aufab_linear", um den Beschleunigungsfaktor "d" zu erhalten.
Dieser Faktor "d" hat die Eigenschaft, dass er bis zur Hälfte der "_ap_richtung_steps"
stetig anwächst und danach wieder stetig abfällt. Die Funktion ist dabei so "austariert",
dass die Summe aller "d" genau wieder "1" ergibt - oder so ähnlich.
Jedenfalls wird "d" in der Folge mit den zuvor kalkulierten Winkel-Deltas multipliziert
und auf die aktuellen Winkel "rotx", "roty" und "rotz" aufaddiert. Auf diese Weise
richtet sich das Raumschiff mit erst zunehmender, dann absinkender Geschwindigkeit
aus. Ganz am Schluss stehen die Winkel "rotx" und "rotz" auf null, während "roty"
exakt auf das anzusteuernde Ziel verweist.
Bei der vergleichsweise geringen Entfernung zum Ziel "_ap_direkt_distance" (10.000 Tkm)
nimmt der Autopilot nicht den Umweg über den Hyperraum, sondern fliegt das Ziel
direkt an. Der "Spot" kommt hier nicht zum tragen, infolgedessen gibt es auch keine
Flugabweichungen; der Autopilot steuert das Raumschiff exakt in die Mitte des
ausgewählten Himmelskörpers.
Profipiloten wie ich verfahren daher gerne folgendermassen: Per Hyper-Move wird das Ziel
grob angeflogen und der Rest wird per Direktflug mittels Autopilot zurückgelegt. Ziemlich
bequeme Sache.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
//Autopilot: Direktflug ---------------------------------
procedure thauptf.ap_direkt;
var
d:double;
begin
//Start
if ap_steps=_ap_direkt_steps then begin
ap_gpb.Position:=ap_gpb.Position-1;
ap_gpb.Max:=2;
ap_steps:=_ap_direkt_steps;
ap_dx:=px/ap_steps;
ap_dy:=py/ap_steps;
ap_dz:=(ap_z-pz);ap_dz:=ap_dz/ap_steps;
ap_spotx:=0;
ap_pb.max:=ap_steps;ap_pb.position:=ap_steps;
dosound(_snd_start,true);
end;
if ap_steps<=0 then begin
ap_gpb.Position:=ap_gpb.Position-1;
taktt.tag:=_ap_ende;
exit;
end;
//Bewegung linear beschleunigen/abbremsen
d:=aufab_linear(0,_ap_direkt_steps-ap_steps,_ap_direkt_steps);d:=d*2;
//mittlere Geschwindigkeit erreicht?
if d>1 then dosound(_snd_slow,true);
//abbremsen?
if(d<1)and(ap_steps<_ap_richtung_steps div 2) then dosound(_snd_bremsen,true);
px:=px-d*ap_dx;
py:=py-d*ap_dy;
pz:=pz+d*ap_dz;
dec(ap_steps);ap_pb.Position:=ap_steps;
end;
Nach "ap_richtung" wird obige Funktion alle 50-tel Sekunden über den universalen Takt
aufgerufen. Wieder wird zuerst geprüft, ob die Funktion in dieser Autopilot-Runde
frisch aktiviert wurde. Ähnlich wie zuvor die Winkel-Deltas werden nun die
Bewegungsdeltas "ap_dx", "ap_dy" und "ap_dz" berechnet, sodass die aktuellen
Positionswerte in "_ap_direkt_steps" Schritten auf null ("px" und "py") bzw. auf
"ap_z-pz" ("pz"; Strecke bis zum Ziel) gebracht werden.
Sind alle Schritte abgearbeitet, wird in die Phase "_ap_ende" gewechselt.
Ansonsten wird mit "aufab_linear" der aus "ap_richtung" bekannte "d"-Faktor
kalkuliert, sodass der Direktflug eine Beschleunigungsphase und Abbremsphase hat.
Bei grösseren Entfernungen zum Ziel schaltet der Autopilot in den Hyper-Move-Modus.
Damit die Geschwindigkeitssteigerung nicht zu krass ausfällt - das würde kein
Raumschiff, geschweige denn menschlicher Pilot aushalten - wird unser Gefährt
in der "ap_hmstart"-Phase erst einmal allmählich auf Touren gebracht.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
//Autopilot: Hyper-Move Beschleunigung --------------------
procedure thauptf.ap_hmstart;
var
vz:integer;
r:integer;
begin
//start
if ap_steps=_ap_hmstart_steps then begin
ap_mark_x:=px;
ap_mark_y:=py;
dosound(_snd_start,true);
end;
//in welcher z-Achsen-Richtung unterwegs?
if(ap_z-pz)>0 then vz:=1 else vz:=-1;
//Ende erreicht?
if ap_steps<=0 then begin
ap_steps:=_ap_hmflug_steps;
taktt.tag:=_ap_hmflug;
exit;
end;
//sich steigerndes Rütteln
px:=ap_mark_x;px:=px+random(3)/(ap_steps+1)-random(3)/(ap_steps+1);
py:=ap_mark_y;py:=py+random(3)/(ap_steps+1)-random(3)/(ap_steps+1);
//Beschleunigung nimmt zu
r:=_ap_hmstart_steps-ap_steps;
pz:=pz+vz*(r*r*r)/10000;
//Turbinen auf Touren?
if ap_steps<_ap_hmstart_steps-20 then dosound(_snd_slow,true);
dec(ap_steps);ap_pb.Position:=ap_steps;
end;
Es wird geprüft, ob die Funktion das erste Mal aufgerufen wurde.
In diesem Fall merkt sich der Computer die aktuelle "px"- und "py"-Position.
Die brauchen wir später, vor Eintritt in den Hyperraum, für die "Dämpfungsfilter".
Dann wird ermittelt, in welche Richtung wir unterwegs sind, ob auf die Sonne zu
oder von ihr weg.
Ist das Ende der "ap_hmstart"-Phase erreicht, hat das Raumschiff also genügend Tempo
gewonnen, dann kann der Autopilot den Sprung in den Hyperraum veranlassen.
Ansonsten wird "pz" exponentiell erhöht und dadurch das Raumschiff sehr stark
beschleunigt. Bedingt durch die Schubkraft unserer Triebwerke kommt es dabei
zu anwachsenden Positionsabweichungen in x- und y-Richtung; da wird unser
Pilot durchgeschüttelt, bis die Zähne klappern.
Der Autopilot schaltet in den Hyper-Move-Modus um, sowie die "ap_hmstart"-Phase
abgeschlossen wurde. Der "Spot" purzelt verstärkt im Visierbereich herum und die
rasende Fahrt durch den Tunnel beginnt mit "ap_hmflug":
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
00041
00042
00043
00044
00045
00046
00047
00048
00049
00050
00051
00052
00053
00054
00055
00056
00057
00058
00059
00060
00061
00062
00063
00064
00065
00066
00067
00068
00069
00070
//Autopilot: Hyper-Move Bremsstrecke berechnen --------------------
function thauptf.ap_bremsen_step_strecke(step:double):double;
begin
result:=(step*step*step)/10000;
end;
function thauptf.ap_spotx_err:double;
begin
result:=ap_spotx*100;
end;
function thauptf.ap_spoty_err:double;
begin
result:=ap_spotx*sin(rotz)*100;
end;
//Autopilot: Hyper-Move Flug durch Tunnel -------------------------
procedure thauptf.ap_hmflug;
function randvz:integer;
begin
if random(2)=0 then result:=1 else result:=-1;
end;
var
r,vz:integer;
begin
//start
if ap_steps=_ap_hmflug_steps then begin
ap_gpb.Position:=ap_gpb.Position-1;
//Rütteln abschwächen
px:=ap_mark_x;
py:=ap_mark_y;
ap_steps:=_ap_hmflug_steps;
ap_dx:=px/ap_steps;
ap_dy:=py/ap_steps;
//in welcher z-Achsen-Richtung unterwegs?
if(ap_z-pz)>0 then vz:=1 else vz:=-1;
ap_dz:=0;
for r:=0 to _ap_hmbremsen_steps do begin
ap_dz:=ap_dz+ap_bremsen_step_strecke(r);
end;
ap_dz:=ap_dz+(abs(ap_spotx_err)+abs(ap_spoty_err))*50;
ap_dz:=(ap_z-pz-vz*ap_dz)/ap_steps;
taktt.tag:=_ap_hmflug;
ap_pb.max:=ap_steps;ap_pb.position:=ap_steps;
dosound(_snd_fast,true);
ap_hmmove_ok:=true;
end;
//Ende
if ap_steps<=0 then begin
ap_steps:=_ap_hmbremsen_steps;
taktt.tag:=_ap_hmbremsen;
ap_hmmove_ok:=false;
exit;
end;
//Flugsprünge und zufällige Flugschwankungen
px:=ap_mark_x-ap_dx+randvz*ap_spotx_err;ap_mark_x:=px;px:=px+random(5)-random(5);
py:=ap_mark_y-ap_dy+randvz*ap_spoty_err;ap_mark_y:=py;py:=py+random(5)-random(5);
pz:=pz+ap_dz;
dec(ap_steps);ap_pb.Position:=ap_steps;
end;
Beim ersten Aufruf der Funktion durch den Universums-Takt wird die Flugposition des
Raumschiffs etwas nachkorrigiert. Dann wird berechnet, wie weit uns der Sprung maximal
ans Ziel heranführen kann, um noch genügend Zeit zum Abbremsen zu haben. Das ist
wichtig. Ohne eine solche Abbremsphase würde der Kandidat nämlich unweigerlich an
der Frontscheibe kleben ...
Ist das Ende des Hyper-Move-Trips erreicht, wird dem Autopiloten folgerichtig mitgeteilt,
dass er mit der Abbremsphase beginnen soll.
Während der Fahrt durch den Tunnel wird das Raumschiff weiter durchgerüttelt. Erschwerend
kommt hinzu, dass der "Spot" im grünen Bereich gehalten werden muss. Schon kleinste
Flugfehler werden bestraft, indem "px" und "py" in unkalkulierbarer Weise modifiziert
werden, was unter Umständen - auf die gesamte Flugstrecke gesehen - ziemlich weit ins
Nirvana führen kann.
Sollten wir den Hyper-Move-Flug durchgehalten haben, ohne unsanft aus dem Hyperraum
hinausgeworfen worden zu sein, verlassen wir diesen wieder auf reguläre Weise, und der
Autopilot beginnt mit der Abbremsphase.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
//Autopilot: Hyper-Move abbremsen -------------------------
procedure thauptf.ap_hmbremsen;
var
vz:integer;
begin
//Start
if ap_steps=_ap_hmbremsen_steps then begin
ap_gpb.Position:=ap_gpb.Position-1;
px:=ap_mark_x;
py:=ap_mark_y;
ap_pb.max:=ap_steps;ap_pb.position:=ap_steps;
dosound(_snd_fastbremsen,false);
end;
//Ende
if ap_steps<=0 then begin
ap_gpb.Position:=ap_gpb.Position-1;
taktt.tag:=_ap_ende;
ap_pb.position:=0;
exit;
end;
//Vorzeichen: Ziel auf Sonne zu oder weg?
if(ap_z-pz)>0 then vz:=1 else vz:=-1;
//abbremsen
ap_dz:=vz*ap_bremsen_step_strecke(ap_steps);
pz:=pz+ap_dz;
//Turbinen gedrosselt?
if ap_steps<40 then dosound(_snd_bremsen,false)
//Turbinen nicht überdreht?
else if ap_steps<_ap_hmbremsen_steps-20 then dosound(_snd_slow,true);
dec(ap_steps);ap_pb.Position:=ap_steps;
end;
Wieder werden zuerst ein paar Korrekturen an unserer Flugposition vorgenommen.
Dann wird geprüft, ob das Raumschiff zum Stillstand gekommen ist. Ist dem so,
wird die Endphase des Autopiloten eingeleitet.
Ansonsten wird "pz" um ein exponentiell abnehmendes Delta modifiziert, d.h.,
das Raumschiff wird zuerst sehr stark, dann immer sanfter abgebremst. Wir wollen
ja unser Mittagessen im Magen behalten.
Zusätzliches Plus: Dank neuster Flugdämpungstechnik - wir haben an nichts gespart - wird
diesmal das Raumschiff nicht mehr so stark durchgerüttelt, sondern gleitet vielmehr
erschütterungsfrei auf sein Flugziel zu - wenn wir denn einigermassen haben
Kurs halten können.
Den Autopiloten kann man jederzeit per Knopfdruck abbrechen. Das hat keinerlei
negativen Folgen. Es sei denn, man befindet sich im Hyperraum - dann haut es einen
aus der Bahn: Wir trudeln wüst durch den Raum, alles wackelt und dreht sich,
die Turbinen kreischen auf, bis endlich auch die letzten Reste an Bewegungsenergie
verpufft sind. Keine angenehme Erfahrung.
Das Gleiche passiert, wenn der "Spot" den "kritischen Bereich" erreicht.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
00030
00031
00032
00033
00034
00035
00036
00037
00038
00039
00040
//Autopilot-Abbruch -------------------------------
procedure thauptf.ap_break;
var
vz:integer;
begin
if ap_steps=_ap_break_steps then begin
ap_mark_z:=ap_dz/_ap_break_steps;
if ap_hmmove_ok then begin
//Abbruch während Hyper-Move
ap_dx:=random(20)-random(20);
ap_dy:=random(20)-random(20);
ap_dz:=random(20)-random(20);
dosound(_snd_break,false);
end
else begin
dosound(_snd_bremsen,false);
end;
end;
//Ende
if ap_steps<=0 then begin
taktt.tag:=_ap_ende;
exit;
end;
//Hyper-Move aktiv?
if ap_hmmove_ok then begin
//unkoordiniert schwingen
rotx:=getangle(rotx+ap_dx);
roty:=getangle(roty+ap_dy);
rotz:=getangle(rotz+ap_dz);
end;
//abbremsen
if(ap_z-pz)>0 then vz:=1 else vz:=-1;
pz:=pz-vz*ap_mark_z;
dec(ap_steps);ap_pb.Position:=ap_steps;
end;
Egal, ob wir den Flug mit Bravour gemeistert haben oder ob es uns aus dem
Hyperraum katapultiert hat, der Autopilot bewahrt stets kühlen Kopf und
leitet am Schluss des Fluges die "ap_ende"-Phase ein.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
//Autopilot ist fertig -----------------
procedure thauptf.ap_ende;
begin
ap_gpb.Position:=0;
taktt.tag:=_ap_stop;
cockpitp.Color:=clblack;
apb.caption:='AutoPilot';
ap_hmmove_ok:=false;
dosound(_snd_stop,false);
end;
In "OGL_Planets" sind diverse Sounds eingebaut, die bei verschiedenen
Situationen abgespielt werden. Leider habe ich keine Ahnung, ob OGL selbst
irgendwelche Sound-Techniken anbietet. Und mit der Windows-API zu DirectSound
habe ich mich bisher auch nie auseinandergesetzt.
Wir benutzten die ziemlich simpel gestrickte Funktion "sndPlaySound",
gekapselt über "dosound". Die Synchronisation war hier das grösste Problem.
Genauer: Es musste dafür gesorgt werden, dass das Geschehen auf dem Bildschirm
sich einigermassen mit der Geräuschkulisse deckt.
So ganz ist mir das nicht gelungen. Manchmal schleicht sich ein "Loop" eines
Sounds ein, wo eigentlich keiner (mehr) hingehört, etwa beim Abbremsen des
Raumschiffs. Dennoch, dafür, dass die ganze Soundmaschinerie mit nur einer
einzigen Prozedur abgedeckt wurde, klingt es recht brauchbar.
00001
00002
00003
00004
00005
00006
00007
00008
00009
00010
00011
00012
00013
00014
00015
00016
00017
00018
00019
00020
00021
00022
00023
00024
00025
00026
00027
00028
00029
//--------------------------------------------------------------
procedure thauptf.dosound(typ:byte;loopok:bool);
var
fn:string;
uflags:cardinal;
begin
if not soundok then exit;
//spielt bereits gleicher Sound?
if typ=snd_typ then exit;
//neuen Sound auswählen
snd_typ:=typ;
case typ of
_snd_stop :fn:='';
_snd_start :fn:='snd_start.wav';
_snd_slow :fn:='snd_slow.wav';
_snd_fast :fn:='snd_fast.wav';
_snd_bremsen :fn:='snd_bremsen.wav';
_snd_fastbremsen:fn:='snd_fastbremsen.wav';
_snd_break :fn:='snd_break.wav';
_snd_teleport :fn:='snd_teleport.wav';
end;
//ewig wiederholen?
uflags:=SND_ASYNC;if loopok then uflags:=uflags or SND_LOOP;
if fn='' then sndPlaySound(nil,0)
else sndPlaySound(pchar(homedir+fn),uflags);
end;
Ach ja, "OGL_Planets" wäre nicht ganz komplett gewesen, wenn dort nicht auch noch einer der
(ge)wichtigsten Protagonisten des Science Fictions untergebracht worden wäre: The one and
only - Miss Piggy! Die hat jetzt nämlich den TV- mit dem PC-Screen getauscht und treibt sich
irgendwo in unserem Solarsystem herum. Den Quellcode dazu habe ich nicht kommentiert. Solche
Schweinereien spielen sich besser im Verborgenem ab. Es stellt sich aber die Frage: Wer hat
die kleine Wutz schon wo gefunden?
Have fun!

Miss Piggy: Ein Schwein im Weltall - irgendwo in den Tiefen des Alls treibt sich Miss Piggy herum. Wo genau, wird nicht verraten. Sucht sie hier etwa nach Kermit? Oder will sie sich nur vor uns verstecken? Wer vermag sie als Erstes aufspüren?
|
|
| Demo-Movie #1: Vorbeiflug an Erde |
|
|
| Demo-Movie #2: Hyper-Move-Flug zur Sonne |
|
|
| Demo-Movie #3: Hyper-Move-Flug zum Saturn |
Im Laufe meines Lebens habe ich Hunderte, wenn nicht Tausende Programme geschrieben.
Aber selten hat es mir so viel Spass gemacht wie bei "OGL_Planets". Die Doku hier ist
zwar wesentlich umfangreicher ausgefallen, als geplant war. Doch wenn man sich den
Source mal rein quantitativ anschaut, ist es eigentlich verblüffend wenig geworden.
Das Verhältnis "Ergebnis" zu "Anzahl Codezeilen" stimmt jedenfalls. Ehrlich, ich kann
mich nicht erinnern, jemals ein besseres "EACV" erreicht zu haben. Rein subjektiv
gesprochen jetzt, mein Chef wäre da sicher anderer Meinung ...
Das Programm hat zweifellos seine Macken. Zum Beispiel bewegt man sich beim Direktflug
im Autopilot-Modus bisweilen rückwärts statt vorwärts. Woran das liegt, habe ich während
der Doku herausgefunden. Geändert habe ich es aber nicht. Überhaupt bin ich über eine
ganze Reihe von Unschönheiten gestolpert, die mir in der aktiven Programmierphase nicht
aufgefallen waren. Auch die Soundeinbindung ist reichlich holprig geraten - vielleicht
etwas zu minimalistisch. Thematisch ist zudem anzukreiden, dass bei den Himmelskörpern
die Grössen oft nicht stimmen. Und sie lungern nur an einer Stelle herum, statt, wie
sich das gehören würde, um die Sonne zu kreisen. Vom Kometenschweif gar nicht zu sprechen;
dieser sieht aus so mancher Blickrichtung echt ätzend aus.
So etwas verdirbt mir jedenfalls nicht den Spass an meinem Proggy. Ist halt nichts
100%iges. But who cares?
"OGL_Planets" wurde mit Delphi 7 programmiert. Der komplette Programmcode, die Texturen,
die Sounds, die EXE und die nötigen OpenGL-DLLs sind alle in diesem ZIP-Archiv verpackt:
OGL-Planets.zip (ca. 1,1 MB)
Das Original-OpenGL-Paket für Delphi habe ich von
"http://www.delphigl.com"
gesaugt. Das ZIP-File des Installers der Version "DGLSDK 2006.1", die ich verwendet habe,
findet ihr hier:
dglsdk-2006-1.zip (ca. 8 MB)