OpenGL Swarm Intelligence

Inhalt

• 1. Vorstoss ins Unbekannte
• 2. Das Projekt OpenGL Swarm Intelligence
  • 2.1. Die Basics
    • 2.1.1. Namensfindung
    • 2.1.2. Ideen zur Realisierung
  • 2.2. OpenGL-Grundgerüst
    • 2.2.1. Verwendung alter OpenGL-Projekte als Muster
    • 2.2.2. Abgespecktes "OpenGL ISS" als Basis
    • 2.2.3. Steuerung im Raum
    • 2.2.4. Ein verdrehtes Problem
    • 2.2.5. Szenerie anzeigen
    • 2.2.6. Dreckige Notlösung für die Textausgabe
  • 2.3. Das erste Partikel
    • 2.3.1. Die TParticle-Klasse
    • 2.3.2. Generierung und Ausgabe des Ein-Partikel-Schwarms
  • 2.4. Der erste Partikelschwarm
    • 2.4.1. Aus einem Partikel mache viele Partikel
    • 2.4.2. Unfreiwillige Addition von Positionsangaben
  • 2.5. Einen erste Reaktionen der Partikel
    • 2.5.1. Auf den Spuren von Moses
    • 2.5.2. Flüchtende Partikel und die Mathematik
    • 2.5.3. Löcher im Schwarm
  • 2.6. Temposteigerung
    • 2.6.1. Sphären sind träge
    • 2.6.2. Dreieckige Polygone als Alternative
    • 2.6.3. Farbverlauf für mehr Plastizität und Natürlichkeit
    • 2.6.4. Mangelhafte Positionierung aufgehoben
  • 2.7. Ausrichtung der Partikel
    • 2.7.1. Dreiecke besitzen eine Richtung
    • 2.7.2. Richtungsvektor zu Rotationsvektor
    • 2.7.3. Rotation um die y-Achse
    • 2.7.4. Und die anderen beiden Achsen?
    • 2.7.5. Alternative: Partikel als richtungslose Punkte
    • 2.7.6. Die rettende Idee - Fluchtvektor wird zum Partikel
  • 2.8. Partikel um den Mittelpunkt rotieren lassen
    • 2.8.1. Wie berechnet man eine Kreisbahn?
    • 2.8.2. Der Einsatz von Sinus und Kosinus klappte nicht
    • 2.8.3. OpenGL-Rotation als mögliche Option
    • 2.8.4. OpenGL-Rotation mit Variationen
    • 2.8.5. Probleme mit Partikelausrichtung und Betrachter-Detektion
    • 2.8.6. Die Kreisbahn muss doch selbst kalkuliert werden
    • 2.8.7. Schwarm-Implosion durch Differenz-Richtungsvektoren
    • 2.8.8. Multiplizierte Orthogonalität
    • 2.8.9. Zweimal das Kreuzprodukt bringt die Lösung
  • 2.9. Zusammenballung des Schwarms
    • 2.9.1. Schwache Schwammsche Schwarm-Schwärmerei
    • 2.9.2. Eigenbewegung der Partikel zum Zentrum hin
  • 2.10. Auseinanderdriften des Schwarms
    • 2.10.1. Partikelverschmelzung unerwünscht
    • 2.10.2. Woher weiss ein Partikel die Position seiner Nachbarn?
    • 2.10.3. Ein Gitterraster zerteilt die Welt
    • 2.10.4. Visualisierung des Gitterrasters
    • 2.10.5. Gitterboxen füllen
• 3. End of Holiday oder: Ein Sprung in der Entwicklung
  • 3.1. Trägheit eines Partikels
  • 3.2. Individualismus eines Partikels
  • 3.3. Weiche Richtungsänderungen
  • 3.4. Verbesserte Dichteflucht
    • 3.4.1. Dichteflucht als Einflussgrösse für den Richtungswechsel
    • 3.4.2. Beschleunigung und Abbremsung
    • 3.4.3. Mehr Volumen bei der Flucht
  • 3.5. Statt nur Beobachterflucht erweiterte Feindesflucht
    • 3.5.1. Anleitung zum Bombenbau
    • 3.5.2. Die erweiterte Feindesflucht
  • 3.6. Kolorierung der Partikel
  • 3.7. Synchronisierung der Partikel
• 4. Fazit
• 5. Video-Demonstrationen von "OpenGL-Swarm" bei YouTube
• 6. Download

1. Vorstoss ins Unbekannte

Es ist Sonntag der 22.01.2012 11:40 Uhr. Seit Tagen schon geistert eine Idee in meinem Kopf herum, die ich nun versuchen werde umzusetzen. Ziel ist es, mithilfe von OpenGL die Simulation eines Partikelstroms zu realisieren, der ein halbwegs intelligentes Fluchtverhalten aufweist. Die einzelnen Partikel sollen sich im Prinzip so verhalten, wie einzelne Fische eines Fischschwarms, wenn sie von einem Fressfeind angegriffen werden.

Anders als bei meinen bisherigen Tutorials beschreibe ich diesmal kein fertiges Produkt, sondern dokumentiere den Entwicklungsprozess fortlaufend mit. Ich weiss also selbst nicht, wo die Reise hingehen wird, ob sie von Erfolg gekrönt sein wird, und ob das ganze Vorhaben überhaupt einen Sinn macht. Aber, wie üblich bei mir, muss es halt heraus, auch wenn es sich als Irrweg erweisen sollte, damit mein Gehirn wieder Ruhe gibt.

2. Das Projekt OpenGL Swarm Intelligence

2.1. Die Basics

2.1.1. Namensfindung

Nun denn, ein neues Projekt sollte einen (vorläufigen) Namen erhalten. Da es unser Ziel ist, eine Art Schwarmintelligenz zu programmieren, die in einer mit OpenGL gestalteten Umgebung agieren soll, ist ein naheliegender Name für das Projekt: "OpenGL Swarm Intelligence". Doch warum die englische Übersetzung von Schwarmintelligenz? Weil englische Projektbezeichnungen eigentlich immer cooler klingen. Und auch eher ein potenziell internationales Publikum ansprechen. Denn wer weiss, wenn sich das Projekt als Erfolg erweist, könnte man später auch noch einen kleinen Film dazu auf YouTube platzieren - und warum sollte man sich hier durch einen deutschen Titel unnötigerweise das internationale Publikum abschrecken?

Okay, Projektname "OpenGL Swarm Intelligence" also. Hauen wir diese drei Wörter in einem nächsten Schritt in Google hinein und schauen, was dabei herauskommt. - Mh ... sieht nicht so gut aus. Mit dem Thema Simulation von Schwarmintelligenz hat sich offenbar bereits so manch andere beschäftigt. Und dies auch noch zu allem Überfluss mithilfe von OpenGL. Aber immerhin, der exakt gleiche Bezeichner tauchte nirgends bei den Suchergebnissen auf, daher belassen wir es vorerst beim aktuellen Projektnamen.

2.1.2. Ideen zur Realisierung

Hier liste ich einmal auf, was mir in den letzten Tagen so zur Umsetzung der Simulation von Schwarmintelligenz eingefallen ist:

• Programmiersprache wird DelphiGL sein. Mit dieser Sprache habe ich in mehreren Projekten bereits positive Erfahrung gemacht.
• Die Umgebung soll zunächst ein komplett leerer Raum sein, in dem sich die Partikel völlig frei bewegen können. Damit uns die Viecher nicht in alle Richtungen abhauen, wird in ihre "genetische Struktur" eingebaut, dass sie den Ursprung des Modells, also die Koordinaten (0,0,0) bevorzugt aufsuchen. In der Realität wäre dies z.B. durch ein Futterangebot an dieser Stelle gegeben.
• Jedes Partikel wird mit individuellem Verhalten ausgestattet. So soll es sich z.B. bei Erkennung eines Feindes von diesem fortbewegen. Die Fluchtrichtung soll logischerweise weg vom Feind weisen. Allerdings nicht immer stur in die genau entgegengesetzte Richtung, weil dies zu mechanisch wirken würde. Die Fluchtrichtung bekommt daher ein Zufallselement mit einprogrammiert.
• Das Schwarmverhalten zeichnet sich dadurch aus, dass sich viele Individuen gleichzeitig in ihren Bewegungen synchronisieren. Unser Partikel sollte also bei seinem Fluchtverhalten stets auch bis zu einem gewissen Grad das Fluchtverhalten seiner Artgenossen berücksichtigen.
• Es gilt: Das Verhalten eines Partikels wird umso stärker von seinen Artgenossen bestimmt, je näher diese sich zu ihm befinden. Dreht der direkte Nachbar nach links, ist dies relevanter, als die Rechtsbewegung eines Partikels, welches sich am Rand des Schwarms befindet.
• Es muss eine Gewichtung berechnet werden, inwieweit das individuelle Verhalten eines Partikels dominiert oder aber das Schwarmverhalten. Sinnvoll klingt hier die Regel: Je näher ein Feind kommt, umso wichtiger wird das individuelle Verhalten, je weiter er weg ist, umso wichtiger wird das Schwarmverhalten.
• Vermutlich muss den Partikeln neben der Ortsliebe zum Ursprung (0,0,0) auch noch eine "Schwarmliebe" einprogrammiert werden. Das heisst, wann immer es einem Partikel möglich ist, sollten es lieber die Nähe des Schwarms aufsuchen als den leeren Raum. Dieses Verhalten kann in gefahrlosen Zeiten gelockert sein, sollte im Falle eines Angriffes von aussen aber Priorität besitzen.
• Die Individuen eines Schwarms in der Natur, etwa Fische oder Vögel, wissen nichts über Mathematik. Man kann auch davon ausgehen, dass sie nicht allzu viel über den kompletten Schwarm an sich wissen, in dem sie sich befinden. Sie können vermutlich nur die Anzahl und das Verhalten ihrer direkten Nachbarn abschätzen. Und in diesem Sinne sollen auch die Partikel in unserem Modell mit möglichst wenig Meta-Wissen ausgestattet sein.
• Die einzelnen Partikel werden als Klasse implementiert. Nennen wir diese doch TParticle. Jedes einzelne Partikel entspricht dann einer Instanz dieser Klasse.
• In einer TParticle-Instanz wird die aktuelle Position des Partikels im Modell vermerkt. Ausserdem seine aktuelle Geschwindigkeit sowie die Richtung, in die es sich gerade bewegt.
• Die Berechnung der Fluchtrichtung und Fluchtgeschwindigkeit wird mithilfe einer inneren Funktion von TParticle vorgenommen. Ich stelle mir dafür so eine Art Punktesystem vor, welches vorgibt, inwieweit sich das Partikel eher individuell oder überindividuell verhält, je nach den äusseren Gegebenheiten.
• Der Schwarm als Ganzes wird wohl auf ein Array von TParticle hinauslaufen. Wobei die Dimensionierung die leichte Erweiterung bzw. Reduzierung der Grösse des Schwarms ermöglicht. Im Idealfall funktioniert der Schwarm mit einem Partikel oder zwei oder drei Partikeln ebenso wie mit Tausenden.

2.2. OpenGL-Grundgerüst

2.2.1. Verwendung alter OpenGL-Projekte als Muster

Da ich bereits mehrere DelphiGL-Projekte realisiert habe, kann ich mich selbst beklauen, um an eine OpenGL-Umgebung zu kommen. Dieses Projekt wird in einen neuen Ordner kopiert, umbenannt und danach von allen Funktionen und Deklarationen befreit, die für das Schwarm-Projekt nicht relevant sind. Das wird einen Moment dauern ...

2.2.2. Abgespecktes "OpenGL ISS" als Basis

So, da bin ich wieder. Als Muster-Projekt diente mir "OpenGL ISS", ein Programm, welches auf dieser Homepage früher schon einmal ausführlich erläutert wurde: Delphi-Tutorial zu "OpenGL ISS"

Dort integriert war nämlich die recht aufwendige Berechnung des Richtungsvektors des Betrachters der Szenerie gemäss der Rotationen der x- y- und z-Achse. Dabei kommt auch wieder die Unit "dan_geo_u.pas" zum Einsatz.

Eliminiert wurden jedoch alle Beschleunigungsfaktoren bei der Berechnung der Geschwindigkeit der Bewegungen. Das heisst, sowie die Cursor-Tasten nicht mehr gedrückt werden, stoppt die Bewegung sofort und wird nicht wie bei "OpenGL ISS" allmählich abgebremst.

Das Malen der Szenerie geschieht (vorerst) weiterhin über einen Timer, der periodisch aufgerufen wird. Durch Änderung der Intervall-Zeit kann so leicht Einfluss auf die Ausgabegeschwindigkeit genommen werden.

Ebenfalls übernommen wurde der Hintergrund, damit man überhaupt etwas von der Bewegung wahrnehmen kann. Die Szenerie spielt sich dadurch innerhalb einer riesigen Sphäre ab, deren Aussenfläche vorerst mit einer Weltraum-Textur versehen wurde.

2.2.3. Steuerung im Raum

Die Steuerung im Raum wird berechnet, wenn der oben erwähnten "frequncy_t"-Timer feuert. Die für die Steuerung relevanten Tastaturereignisse wurden zuvor in den globalen Variablen "a_key" und "a_ctrl" gesichert. Die zur Berechnung des Look-Vektors (also des Richtungsvektors des Betrachters in die Szenerie hinein) benötigten Funktionen sind in der Unit "dan_geo_u.pas" definiert. Eine Erläuterung hierzu findet sich im Delphi-Tutorial "OpenGL ISS".

Die Steuerung ist knackig klein und elegant formuliert, wie ich finde. Im Wesentlichen wird nur der Richtungsvektor bestimmt, der wiedergibt, in welche Richtung der Anwender gerade schaut. Dieser Richtungsvektor wird mit einem konstanten Wert entweder verlängert oder verkürzt, je nach Richtung, in die geflogen werden soll. Zuletzt wird der so berechnete Richtungsvektor zum aktuellen Positionsvektor des Betrachters ("my_position_v") hinzuaddiert, und schon ist die neue Position im Raum bestimmt. Anschliessend wird unter diesen Bedingungen die Szenerie über "draw_scene" neu berechnet.

2.2.4. Ein verdrehtes Problem

Mh ... wie mir eben auffiel, ist die Steuerung doch noch reichlich suboptimal. Bewege ich mich nämlich in der Ausgangssituation nach links, dann drehe ich mich korrekt im Raum um die eigene Achse, d.h. um die y-Achse. Wenn ich nun aber senkrecht nach oben schwenke, mich also 90 Grad um die x-Achse drehe, dann verläuft die y-Achse parallel zu meiner Sichtrichtung. Drehe ich mich nun nach links, resultiert daraus eine Kreiselbewegung, die so eigentlich nicht gewollt ist. Stimmig wäre es erst, wenn sich meine Drehung nicht an den absoluten Achsen des Modells orientieren würde, sondern am Richtungsvektor und den dazu orthogonalen Achsen. Nun ja, dass schauen wir uns vielleicht später noch einmal näher an.

2.2.5. Szenerie anzeigen

Unsere Welt wird über den "freqwuency_t"-Timer permanent neu gezeichnet. Und dazu wird die Prozedur "draw_scene" aufgerufen:

Es werden zunächst ein paar Grundeinstellungen am OpenGL-Modell vorgenommen und der Grafikpuffer geleert. Mit "glLoadIdentity" wird der Betrachter imaginär an den Ursprung positioniert. Anschliessend werden die Rotationen und Positionsänderungen ausgeführt, die der Benutzer vollführt hat, und zwar gerade in negierter Weise - denn nicht der Betrachter bewegt sich (der hockt ja starr vor dem Monitor), sondern das Modell. Die Prozedur "draw_space" kopiert die Sphäre der Raumkugel in den Grafikpuffer. Zuletzt werden dann die genauen Positionsangaben noch auf dem Panel "status_p" ausgegeben.

Grundgerüst von OpenGL Swarm Intelligence: Wir befinden uns noch in einem grossen, leeren Raum, dessen Ränder durch eine Textur kenntlich gemacht wurden. Wir können uns bereits mittels der Cursor-Tasten und mithilfe der STRG-Taste in alle Richtungen bewegen.

2.2.6. Dreckige Notlösung für die Textausgabe

Das grösste Problem bei dieser Prozedur war für mich eigentlich die Textausgabe. Denn eigentlich wollte ich nicht auf ein Panel schreiben, sondern direkt in den Grafikpuffer von OpenGL. Ich habe aber eben auf die Schnelle nichts im Web gefunden, worüber sich dieses realisieren liesse. Seltsamerweise. Nun denn - stellen wir das erst einmal zurück.

2.3. Das erste Partikel

2.3.1. Die TParticle-Klasse

Ausgehend von unseren früheren Überlegungen im Kapitel 2.1.2 Ideen zur Realisierung bauen wir nun eine Klasse "TParticle" auf, die alle Eigenschaften eines Partikels kapselt. Spontan fällt mir dazu nur ein, dass die Positionsangaben im Raum benötigt werden. Auch ein Bezeichner "quad" für die OpenGL-Objekt-ID wird deklariert. Und dann natürlich noch eine Prozedur "draw" für die Ausgabe des Partikels auf dem Bildschirm. Das ergäbe dann in etwa so etwas:

Wie wir im Konstruktor sehen, verpassen wir dem Partikel zu Beginn eine Zufallsposition im Raum, die irgendwo innerhalb eines Radius von 50 Metern rund um den Ursprung herum liegt. Ausserdem bekommt das kugelförmige Partikel eine Grösse von einem Meter zugewiesen (zweiter Parameter bei "gluSphere").

2.3.2. Generierung und Ausgabe des Ein-Partikel-Schwarms

Nun müssen wir die TParticle-Klasse in unser Modell integrieren. Dazu bietet sich ein Array aus TParticle-Elementen an, welches wir vorerst mit nur einem einzigen Element füllen wollen. Die Initialisierung des Arrays geschieht bei "FormCreate" und die Zerstörung in "FormDestroy". Die Ausgabe aller Partikel erfolgt direkt nach der Ausgabe der Raum-Sphäre.

Das erste Partikel: Wir haben unser erstes Partikel generiert. Per Zufall wird es irgendwo in der Nähe des Ursprungs generiert. Dieses Exemplar liegt in 10 Metern Entfernung direkt vor uns. Wir können, Dank OpenGL, bereits jetzt schon zu ihm fliegen und es aus allen Richtungen betrachten.

2.4. Der erste Partikelschwarm

2.4.1. Aus einem Partikel mache viele Partikel

Der Source zur Generierung und Ausgabe unseres Einzelpartikels, den wir im vorherigen Kapitel kennenlernten, ist schlauerweise von vorneherein dafür ausgelegt worden, nicht nur ein Partikel, sondern beliebig viele Partikel im Array "particle_a" zu verwalten. Alles, was wir machen müssen, um z.B. 100 Partikel zu erzeugen, ist die Konstante "_particle_max" auf 100 zu setzen. Schauen wir uns das Ergebnis an:

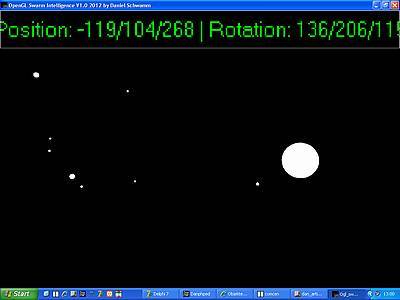
Der erste Partikelschwarm: Nur durch Änderung einer Konstante haben wir aus unserem Einzelpartikel exakt 100 Partikel gemacht, die zufällig verteilt im Raum um uns herum schweben. Allerdings können bisher nur wir uns bewegen, die Partikel selbst ändern ihre Position noch nicht.

2.4.2. Unfreiwillige Addition von Positionsangaben

Unser Schwarm sieht schon ganz hübsch aus. Betrachtet man jedoch die Koordinatenangaben im Kopf-Panel, dann sieht man, dass wir uns an einer Position im Raum befinden, an der es eigentlich gar keine Partikel mehr geben dürfte (-119/104/268). Geplant hatten wir doch, dass diese sich innerhalb eines Radius von nur 50 Metern rund um den Ursprung bewegen.

Mir wurde bald klar, worin der Grund für die falsche Positionierung liegt. OpenGL zeichnet immer relativ von der letzten Position aus weiter. Wird also ein Partikel an Position (20,0,0) gezeichnet, dann landet das nächste Partikel mit Position (40,0,0) nicht an dieser absoluten Stelle, sondern relativ zur vorherigen Position bei Koordinate (20+40,0,0). Um die relative Positionierung zu verhindern, gibt es die OpenGL-Befehle "glPushMatrix" und "glPopMatrix". Diese sorgen dafür, dass nach einer Malaktion stets wieder von der vorherigen Position ausgegangen wird, was in unserem Fall dem Ursprung entspricht. Wir müssen also "draw" von TParticle noch ein klein wenig erweitern:

Korrigierter Partikelschwarm: Bei diesem Beispiel wurde die Anzahl der Partikel auf 1.000 erhöht. Sie sind jetzt nur noch 10 cm im Radius gross, etwa so wie dicke Fische. Die zufällige Positionierung wurde auf 10 m um den Ursprung reduziert. Und voilà, das Ergebnis sieht schon eher so aus, wie es einem Schwarm geziemt.

2.5. Einen erste Reaktionen der Partikel

2.5.1. Auf den Spuren von Moses

Einen Moment lang wusste ich eben nicht, wie fortfahren. Angesichts des recht dichten Partikelschwarms, den wir bereits generieren können, stellte ich mir dann aber vor, dass es sicher cool aussähe, wenn wir durch diesen hindurchfliegen und die Partikel sich daraufhin alle vom Betrachter wegbewegen. Wir würden damit also quasi den Schwarm der Partikel teilen wie einst Moses das Rote Meer.

Dazu ist eine neue Prozedur von TParticle nötig. Nennen wir sie "calc_position". Diese rufen wir unmittelbar vor dem Zeichnen eines jeden Partikels auf. Darin wird dann anhand der Nähe des Betrachters ermittelt, ob und wie eine Ausweichbewegung initiiert werden muss. Entsprechend wird dann "postion_v" modifiziert.

2.5.2. Flüchtende Partikel und die Mathematik

Na, das habe ich eben aber wieder locker angekündigt, diese Flucht der Partikel vor dem Betrachter. Denn sinnvollerweise bewegen sich die Partikel dann in die genau entgegengesetzte Richtung. Ist das Partikel direkt vor dem Betrachter, dann flieht es also tiefer in den Raum hinein. Das ist noch einfach zu kalkulieren, denn dies entspricht ja genau dem Richtungsvektor des Betrachters "look_vector". Komplizierter wird es aber, wenn sich Partikel seitlich vom Betrachter befinden. Hier muss idealerweise ein Vektor bestimmt werden, welcher die Richtung zwischen Partikel und Betrachter wiedergibt. Das Partikel müsste dann für die optimale Flucht nur noch gemäss dieses Richtungsvektors seine Position ändern. Nur, wie ermittle ich den gesuchten Richtungsvektor?

Da stand ich echt eine Weile auf dem Schlauch. Ich wusste zwar, ich kann den Winkel zwischen zwei Punkten berechnen, denn dazu gibt es eine Funktion in der "dan_geo_u"-Unit, nämlich "v_angle". Doch diese Funktion liefert als Ergebnis einen Skalar zurück, also einen Einzelwert. Doch was bringt der mir? Wie mache ich daraus dann einen Vektor?

Letztlich half mir Google auf die Sprünge. Nach mehreren Versuchen hatte ich endlich eine geeignete Suchanfrage formuliert: "Richtungsvektor zwischen zwei Punkten". Gleich einer der ersten Treffer führte mich auf die Webseite http://www.rither.de/. Dort stand peinlicherweise, dass die Berechnung des Vektors zwischen zwei Punkten zu den einfachsten Aufgaben in der Geometrie gehört. Und das stimmte auch. Man erhält den gesuchten Vektor nämlich schlicht durch eine Subtraktion der Punktvektoren. Na, dann wollen wir doch einmal schauen, ob das wirklich so stimmen kann!

2.5.3. Löcher im Schwarm

Um die Fluchtrichtung eines Partikels zu berechnen, benötigen wir einen Richtungsvektor. Dieser ergibt sich laut vorherigem Abschnitt durch Subtraktion der Partikelposition von der Betrachterposition. Weiterhin soll gelten: Je näher der Betrachter kommt, umso ausgeprägter soll die Fluchtrichtung eingeschlagen werden. Und um das Ganze optisch noch etwas attraktiver zu gestalten, werden zudem die Partikel mit verschiedenen Farben versehen.

Zunächst erweitern wir die TParticle-Klasse um drei Fliesskommazahlen, die bei "create" mit zufälligen Werten gefüllt werden. Diese Variablen dienen als Übergabewerte für die OpenGL-Prozedur "glColor3f" in der "draw"-Prozedur. Dadurch werden die Partikel farbig wiedergegeben.

In "calc_position" wird zunächst mithilfe der "v_distance"-Funktion aus der "dan_geo_u"-Unit der Abstand zwischen Partikel und Betrachter ermittelt. Liegt dieser über fünf Meter, dann wird die Prozedur wieder verlassen. Ansonsten wird eine Fluchtbewegung des Partikels vorgenommen. Aus dem Abstand zum Betrachter wird über eine Formel die Fluchtgeschwindigkeit berechnet. Den Fluchtvektor berechnen wir durch Subtraktion der Partikelposition von der Betrachterposition. Der sich so ergebene Fluchtvektor wird mit der genormten Fluchtgeschwindigkeit skaliert. Und zuletzt wird der Fluchtvektor zum Positionsvektor addiert, wodurch sich die neue Position des Partikels ergibt.

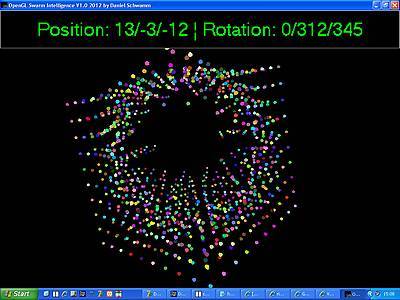
Fluchttunnel durch den Partikelschwarm: Hier kann man sehen, wie sich der Betrachter durch den Partikelschwarm bewegt hat. Die Partikel in seiner Nähe sind ihm aus dem Weg gegangen, während die weiter entfernten Partikel ihre Position nicht verlassen haben.

2.6. Temposteigerung

2.6.1. Sphären sind träge

Mein PC muss bei 1.000 Partikeln schon kämpfen, bei 10.000 Partikeln geht er regelrecht in die Knie. Aber andere OpenGL-Programmierer schaffen es, sogar noch wesentlich mehr Partikel flüssig zu animieren. Wie machen die das? Der Grund für die Trägheit unserer Partikel ist eigentlich klar und den hatte ich auch schon die ganze Zeit im Hinterkopf: Die Sphären, die wir über den OpenGL-Befehl "gluSphere" generieren, sind relativ komplexe Objekte, deren Berechnungen entsprechend viel CPU-Power verschlingen.

2.6.2. Dreieckige Polygone als Alternative

Auf der Suche nach weniger aufwendigen Partikeln stiess ich rasch auf Polygone. Diese lassen sich durch die Angabe ihrer Eckpunkte, den Vertices, relativ exakt definieren. Ich entschied mich für nur drei Eckpunkte, wodurch dreieckige Flächen entstanden, die man mit etwas Fantasie als Fische interpretieren kann. Und das wäre ja für ein Schwarm-Partikel nicht die ungünstigste Form. Unsere "Fisch"-Polygone erhalten übrigens eine Länge von 20 cm und eine Höhe von 6 cm; die Ausmasse eines Standard-Fisches halt. Ansonsten sind sie flach wie Flundern. Dadurch, dass wir von nun an mit Vertices arbeiten, kann das Objekt "quad" aus der TParticle-Klasse eliminiert werden.

2.6.3. Farbverlauf für mehr Plastizität und Natürlichkeit

Ebenfalls wieder entfernt wurden die drei Farbwerte für Rot, Grün und Blau aus der TParticle-Klasse. Dies Farbe berechnen wir nämlich jetzt innerhalb der "draw"-Prozedur selbst, und zwar anhand der Distanz zum Betrachter. Verwendet werden nur Grüntöne, wobei gilt, je weiter das Partikel vom Betrachter entfernt ist, umso dunkler wird es dargestellt. Die ehemalige Prozedur "calc_position" wurde dafür zur Funktion, die uns den Distanzwert zurückliefert.

2.6.4. Mangelhafte Positionierung aufgehoben

Ausserdem stolperte ich eben über einen dicken Fehler, der mir bisher nicht aufgefallen war. Bei der zufälligen Positionierung der Partikel wurden ganzzahlige Zufallswerte generiert, was zur Folge hatte, dass die Partikel anfangs alle einen Mindestabstand von einem Meter zueinander hatten. Dadurch war auch die Wahrscheinlichkeit gross, dass verschiedene Objekte den gleichen Ort einnahmen. So sah man letztlich viel weniger Objekte, als tatsächlich berechnet wurden. Die "create"-Prozedur wurde entsprechend verbessert.

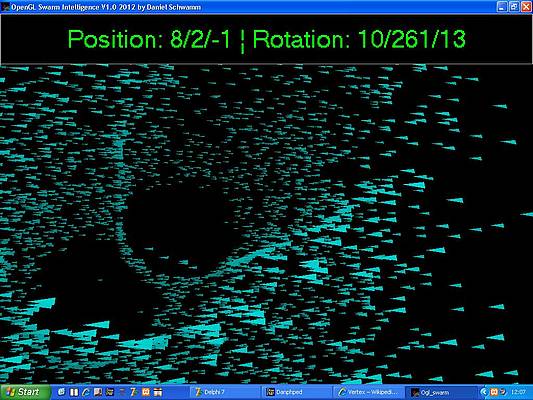
Schneller Partikelschwarm aus Polygonen: Die Verwendung von Polygonen statt Sphären für die Partikel erlaubt eine erheblich schnellere Wiedergabe des Schwarms. Die Partikel wurde zudem so eingefärbt, dass sie umso dunkler werden, je weiter sie vom Betrachter entfernt sind. Der Schwarm ähnelt damit immer mehr einem natürlichen Schwarm aus Fischen.

2.7. Ausrichtung der Partikel

2.7.1. Dreiecke besitzen eine Richtung

Durch die Verwendung von Polygonen wurde die Zeichengeschwindigkeit unseres Schwarms enorm gesteigert. Leider besitzen die Polygone aber anders als Sphären eine Richtung. Es ist also für die physikalische Korrektheit nötig, die Partikel mit der Spitze in die Richtung weisen zu lassen, in die sie sich bewegen. Damit haben wir uns aber ein ziemliches Problem aufgehalst.

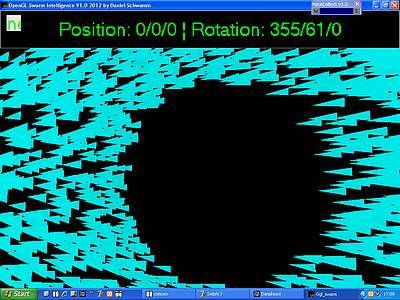
Alle Partikel zeigen in die gleiche Richtung: Obwohl wir uns durch den Schwarm bewegt haben und jedes Partikel für sich auch in die korrekte Richtung geflohen ist, so weisen doch alle Partikel mit der Spitze in die gleiche Richtung. Das entspricht so natürlich nicht den von Fischen gewohnten Gegebenheiten. Das muss noch geändert werden. Nur wie?

2.7.2. Richtungsvektor zu Rotationsvektor

Autsch! Hier machten sich einmal wieder meine bisweilen eingerosteten bzw. mangelnden mathematischen Kenntnisse schmerzlich bemerkbar. Die Fluchtrichtung der Partikel haben wir ja bereits in einem Richtungsvektor ermittelt. Wir wissen also im Prinzip, in welcher Richtung die Spitze des Partikels weisen müssten. Da wir jedes Partikel einheitlich malen, und zwar vom Ursprung aus gesehen als Dreieck, dessen Spitze tiefer in den Raum weist, müssen wir jedes Partikel einzeln in seine Bewegungsrichtung rotieren lassen. Der OpenGL-Befehl "glRotatef" bietet sich dafür ja ganz offenkundig an. Nur, der erwartet eine Winkelangabe für jede Achse. Doch wie kalkulieren wir aus dem gegebenen Richtungsvektor die passenden Winkel, um daraus den geforderten Rotationsvektor zu bilden?

Diesmal wurde ich im Web nur wenig fündig. Mir fiel aber selbst wieder ein, dass man den Winkel in einem rechtwinkligen Dreieck dadurch berechnen kann, indem man die Höhe durch die Breite teilt. Dieser Wert entspricht der Steigung der Geraden, also der Hypotenuse. Füttert man die Arcustangens-Funktion mit der Steigung, dann erhält man ihren Winkel - allerdings im Bogenmass, nicht in Grad. Ein Umstand, der mich noch einmal etliche Minuten meines Lebens gekostet hat, bis ich es endlich registriert hatte.

2.7.3. Rotation um die y-Achse

Folgender Source wird verwendet, um den Winkel des Fluchtvektors zu berechnen, der nötig ist, damit unser Partikel in gewünschter Weise um die y-Achse rotiert werden kann:

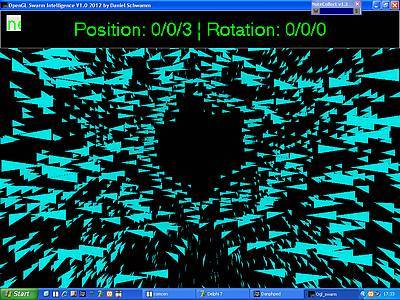
Rotation der Partikel um die y-Achse: Als wir uns durch den Schwarm bewegten, wurden die Partikel in der Gefahrenzone gezwungen, sich in eine andere Richtung zu bewegen. Diese Bewegungsrichtung lässt sich nun sehr schön und naturgemäss an ihrer Spitze erkennen.

2.7.4. Und die anderen beiden Achsen?

Die Rotation um die y-Achse in Bewegungsrichtung funktionierte korrekt, soweit ich das überblicken konnte. Als ich nun jedoch das Gleiche mit der x- und z-Achse Achse versuchte, klappte es leider nur manchmal, aber nicht immer. Der Grund dafür ist mir nicht klar, aber ich vermute einmal, es hat mit der Rotationsreihenfolge der Achsen zu tun, mit falschen Formeln und meinem beschränktem Verständnis für die gesamte Materie.

Um überhaupt abschätzen zu können, in welche Richtung die Partikel genau zeigen müssten, wenn es mathematisch korrekt zu geht, habe ich bei folgendem Beispiel jeden Partikel-Fluchtvektor mit ins Modell eingezeichnet. Was eigentlich auch ziemlich cool aussieht, oder? Allerdings zeigt sich jetzt auch überdeutlich, dass irgendetwas mit unserer Rechnung noch nicht so ganz stimmen kann.

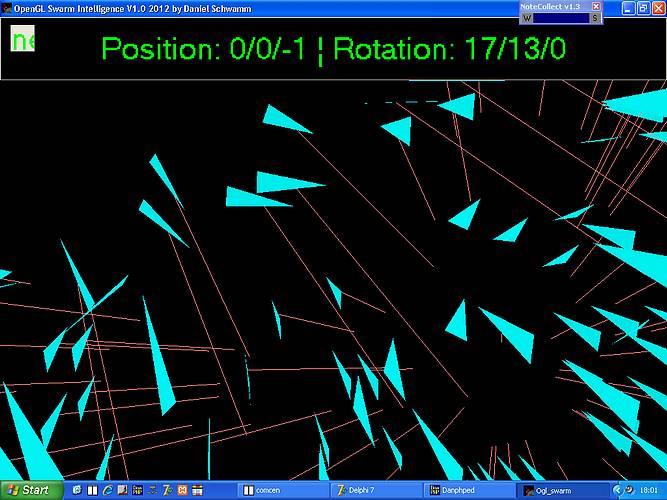
(Fehlerhaft) ausgerichtete Partikel mit Fluchtvektor: Wieder sind wir durch den Schwarm geflogen, und wieder sind die Partikel nach allen Seiten davon gerauscht. Anhand der roten Fluchtvektoren erkennt man aber auch, das nicht wenige Partikel trotz der berechneten Achsenrotationen noch immer in die falsche Richtung weisen.

2.7.5. Alternative: Partikel als richtungslose Punkte

Aaaargh!

Einen ganzen verdammten Tag habe ich mich mit der Ausrichtung der Partikel beschäftigt, ohne auf einen grünen Zweig zu komme. Zwischenzeitlich habe ich die Polygone sogar durch Punkte ersetzt, die mittels des OpenGL-Befehls "glPointSize" bei Annäherung in passend grosse quadratische Flächen transformiert wurden. Das funktionierte auch gut und schnell, aber rein optisch gefallen mir die "Fisch"-Partikel halt eindeutig besser.

Dennoch sei hier kurz gezeigt, wie die Points gezeichnet wurden:

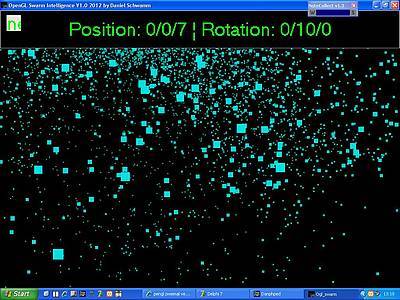
Partikel als richtungslose Punkte: Um den Schwierigkeiten der Ausrichtung der dreieckigen Partikel zu umgehen, wurden sie versuchsweise als Punkte gezeichnet, die sich bei Annäherung vergrössern. Diese Vorgehensweise wurde aber wieder rückgängig gemacht, da die Fisch-Partikel einfach cooler aussehen.

2.7.6. Die rettende Idee - Fluchtvektor wird zum Partikel

Dann fiel mir jedoch zum Glück endlich auf, dass ich bereits weiter oben durchaus in der Lage war, die Fluchtvektoren ins Modell einzuzeichnen. Und zwar alleine unter Verwendung des Richtungsvektors, d.h. ohne jede Rotation. Ich müsste also nur statt einer Linie ein dreieckiges Polygon berechnen, dann hätte ich doch genau die korrekt ausgerichteten Partikel! Und hier ist auch schon der Source dazu, der mich ganz anders als die Rotationsgeschichte nur einige wenige Minuten Arbeit gekostet hat:

Der Source zur Winkelberechnung für die Achsen-Rotation des Partikels in Funktion "calc_position" wurde eliminiert.

In der Prozedur "draw" wird zunächst der Fluchtvektor normiert, d.h., auf eine Länge von 1 gebracht. Danach wird er durch Skalierung auf die Partikel-Länge reduziert. Anschliessend wird der Fluchtvektor mit dem Positionsvektor addiert, wodurch wir die Position der Spitze des Partikels erhalten. Zuletzt wird dann noch das Polygon gezeichnet, und zwar von der Partikelposition bis zur berechneten Spitze.

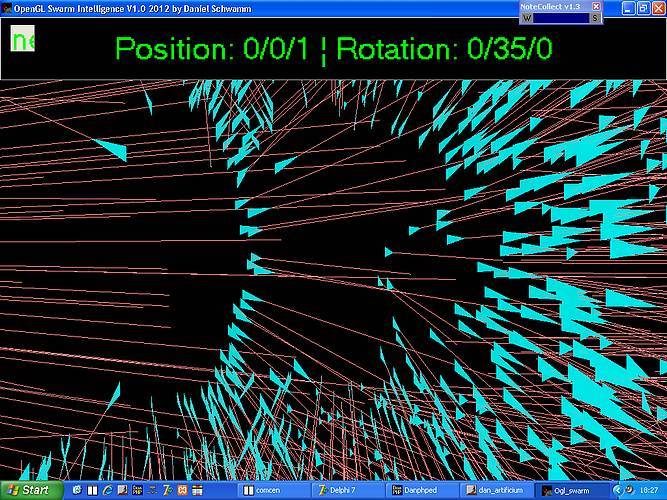
Korrekt ausgerichtete Partikel mit Fluchtvektor: Basierend auf dem Fluchtvektor werden die Partikel ohne Rotation direkt perspektivisch korrekt gezeichnet. Dadurch sind alle Partikel gemäss ihre Bewegung ausgerichtet. Und die roten Richtungsvektoren schauen jetzt aus wie Laserstrahlen, die aus kleinen Raumschiffen abgeschossen werden.

2.8. Partikel um den Mittelpunkt rotieren lassen

2.8.1. Wie berechnet man eine Kreisbahn?

Das nächste Vorhaben ist, den Partikeln eine Eigenbewegung zu geben. Und zwar sollen sie zunächst ganz simpel um den Ursprung kreisen. Doch wie stellen wir das an? Wir haben gesehen, dass wir den Ortsvektor mit dem Richtungsvektor addieren müssen, um eine Bewegung zu simulieren. Ziel müsste also sein, einen passenden Richtungsvektor zu berechnen, wodurch das Partikel auf eine Kreisbahn gezwungen wird.

2.8.2. Der Einsatz von Sinus und Kosinus klappte nicht

Schnell zeigte sich jedoch, dass dies gar nicht so einfach ist. Obwohl uns eigentlich alle nötigen Werte vorliegen. Der Radius ergibt sich durch die Länge des Positionsvektors. Als Winkelzuwachs wollen wir jeweils einen Grad nehmen. Die Formeln für die Drehung im zweidimensionalen Raum habe ich noch im Kopf. Die Winkel-Variable "periode" wird bei jeder Aktualisierung des Modells um einen Grad nach oben gezählt wird. Daraus basteln wir uns also einmal Folgendes zusammen:

Okay ... die Partikel drehen sich durchaus. Aber nicht um den Mittelpunkt, sondern in sehr unvorhersehbarer Weise. Mh ... da müssen wir wohl nachbessern.

2.8.3. OpenGL-Rotation als mögliche Option

Ich experimentierte noch sehr viel mit den Parametern und Formeln für die Rotation herum, bekam aber nie das gewünschte Ergebnis.

Doch warum sollen wir eigentlich alles selber machen? OpenGL verfügt ja bereits über den Befehl "glRotatef". Den rufen wir jetzt einmal jeweils direkt vor dem Zeichnen eines Partikel auf, um so den "Zeichenstift" im Modell an die gewünschte Stelle zu platzieren. Mal schauen, was dabei herauskommt ...

Na bitte! Das klappte ja auf Anhieb. Alle Partikel drehten sich nun brav und synchron um den Ursprung herum.

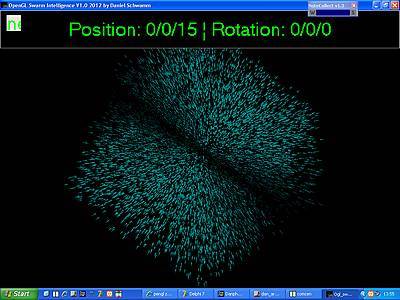
Synchrone Partikel-Rotation mittels OpenGL-Befehl: Dank mächtiger OpenGL-Befehle werden hier ohne Einsatz komplizierter Formeln alle Partikel um den Ursprung rotiert.

2.8.4. OpenGL-Rotation mit Variationen

Um das aktuelle doch sehr statische Rotationsverhalten des Schwarms etwas aufzubrechen, variieren wir den Winkel in Abhängigkeit zum Abstand des Betrachters. Wenn wir also in den Schwarm hineinfliegen, sollten sich die Bewegungsmuster der einzelnen Partikel ändern. Verstärkt wird der Effekt noch, indem die Betrachter-Detektion wieder aktiviert wird, die dafür sorgt, dass die Partikel ausweichen und so auf neue Bahnen gelangen. Der Single-Wert "angle" wird zusätzlich in die TParticle-Klasse mit aufgenommen.

Wow! Ja, das Ergebnis kann sich wirklich sehen lassen. Was allerdings durch ein Einzelbild nur sehr unvollkommen wiedergegeben werden kann.

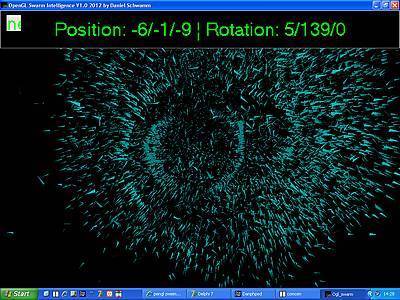
Partikel-Rotation mittels OpenGL-Befehl und variierenden Variablen: Unser Schwarm rotiert mit verschiedenen Geschwindigkeiten um das Zentrum und weicht dem Betrachter aus. Es ergeben sich dadurch sehr schöne Muster, die bis zu einem gewissen Grad durchaus an einen echten Fischschwarm erinnern.

2.8.5. Probleme mit Partikelausrichtung und Betrachter-Detektion

Wie man sieht, rotieren die Partikel zwar fleissig um das Zentrum, doch ist ihr Spitze wieder nicht zur Bewegungsrichtung ausgerichtet. Vielmehr behalten die Partikel beständig ihre Ursprungs- bzw. letzte Fluchtrichtung bei.

Ausserdem hat sich erwiesen, dass die Betrachter-Detektion teilweise nicht funktioniert. Der (mögliche) Grund hierfür: Die Teilchen befinden sich durch die OpenGL-Rotation innerhalb des Modells womöglich an einem anderen Ort, als dem, den wir ursprünglich für sie berechnet haben. Obwohl also ein Partikel direkt vor dem Betrachter erscheint, muss die Ausweichbewegung nicht initiiert werden, weil die Partikelposition u.U. etliche Meter entfernt berechnet wurde.

2.8.6. Die Kreisbahn muss doch selbst kalkuliert werden

Teufel aber auch! Ohne die konkrete Berechnung des Orts und der Richtung eines Partikels funktionieren die bereits entwickelten Mechanismen der Ausrichtung und Betrachter-Detektion nicht. Also müssen wir uns wohl oder übel doch mit der Berechnung der Kreisbahn um den Ursprung herum befassen. Doch erneut stellt sich jetzt die Frage: wie herangehen?

Die nötigen Berechnungen der Kreisbahnen eines Partikels haben mich einen ganzen Tag gekostet. Es scheint bei OpenGL-Programmieren irgendwie Konsens zu sein, sich nicht selbst mit diesen Dingen zu befassen, sondern so wie wir zuvor dafür OpenGL-Kommandos zu verwenden. Daher war im Web auch keine Lösung dafür zu finden.

2.8.7. Schwarm-Implosion durch Differenz-Richtungsvektoren

Erst nach etlichen Stunden kam mir die Idee, dass ein Partikel, welches sich in einer Kreisbahn bewegt, stets einen Winkel von 90 Grad zum Ursprung halten muss. Befindet es sich also am Punkt A und soll 1 cm weit fliegen, dann müsste der neue Punkt B in Flugrichtung und um 90 Grad versetzt zum Ursprung hin liegen. Wir müssen uns also einen Richtungsvektor ermitteln, der aufaddiert zum Punk A den Punkt B ergibt.

Erneut drohte ich an dem Problem zu scheitern. Folgenden Ansatz hatte ich aber bereits ausklamüsert: Wir betrachten den Positionsvektor als Richtungsvektor zum Ursprung. Der Fluchtvektor beschreibt die aktuelle Flugrichtung. Ziehen wir beide Vektoren voneinander ab, erhalten wir einen neuen Richtungsvektor, der genau zwischen den beiden liegt. Leider verweist dieser Richtungsvektor jedoch nicht auf einen Punkt 90 Grad versetzt zum Nullpunkt, sondern wandert bei jeder Neuberechnung sehr schnell direkt auf den Ursprung zu. Die Folge: Unser Schwarm implodiert! Das allerdings sieht recht cool aus.

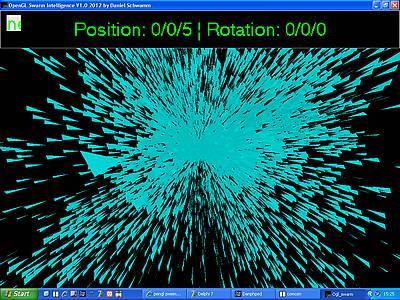
Implosion des Schwarms durch Richtungsvektoren auf den Ursprung: Wird der neue Richtungsvektor eines jeden Partikels zwischen Ursprungsvektor und aktuellen Richtungsvektor gelegt, so zeigt er nach ein paar Iterationsschritten direkt auf den Ursprung. Und der Partikelschwarm wird dann vom Zentrum aufgesogen wie von einem schwarzen Loch.

2.8.8. Multiplizierte Orthogonalität

Besonders bitter ist, dass ich anfangs schon fast die richtige Idee zur Lösung des Problems hatte, nämlich einen Richtungsvektor zu finden, der senkrecht auf dem Positionsvektor steht. Aus meiner "dan_geo_u"-Unit wusste ich, dass man mithilfe des Kreuzprodukts einen orthogonalen Vektor auf die durch zwei Vektoren aufgespannte Fläche erhält. Diese Fläche ergibt sich ja aus Positionsvektor und Fluchtvektor. Doch der aus dem Kreuzprodukt berechnete Vektor stand zwar senkrecht zur Fläche, wies aber im dreidimensionalen Raum in eine ganz andere Achse hinein als in die, in der wir uns bewegen mussten. Was wir benötigten, wäre eigentlich noch einen orthogonalen Vektor zum Kreuzprodukt-Vektor, dann würde die Richtung wieder stimmen.

Oh Mann! Da hatte ich die Lösung schon im Kopf, schaltete aber einfach nicht. Und so verbrachte ich erneut etliche Stunden im Web, ohne eine Lösung für mein Problem finden zu können. Im Gegenteil, dass, was ich fand, behauptete sogar, den einen gesuchten 90-Grad-Vektor zum Positionsvektor gibt es gar nicht, weil es deren ja für eine Gerade unendlich viele gibt (ich allerdings fand nicht einmal einen).

Erst am nächsten Tag stellte ich endlich die richtige Frage an Google, bei der die entscheidenden Wörtchen "Dreieck" und vor allem "Höhenvektor" vorkamen. Das führte mich auf diese Seite: http://www.matheboard.de/archive/11405/thread.html

Hier fragt ein Schüler (?) nach einer Methode zur Berechnung des Höhenvektors. Und er bekommt prompt kompetente Antwort: Berechne das Kreuzprodukt aus den Vektoren AB und AC des Dreiecks ABC und du erhältst einen darauf senkrecht stehenden Vektor v. Bilde nun aus diesem Vektor v und dem Positionsvektor AB erneut das Kreuzprodukt und es ergibt sich der gesuchte Höhenvektor des Dreiecks ABC.

Aaaaarg!

Kreuzprodukt zweimal anwenden! Natürlich! Genau das habe ich am Vortag doch sogar selbst angedacht. Allerdings dann dämlicherweise nicht weiterverfolgt. Daniel, Daniel, du wirst zu unflexibel auf deine alten Tage.

2.8.9. Zweimal das Kreuzprodukt bringt die Lösung

Na, jetzt wollen wir aber wissen, ob das tatsächlich hinhaut. Wir berechnen also den neuen Fluchtvektor folgendermassen:

Alle Partikel haben zu Beginn eine Richtung erhalten. Diese Richtung behalten sie nach obiger Formel auch bei, nur dass sie sich jetzt kreisend um das Zentrum bewegen. Dadurch schwimmen die "Fische" nicht synchron, sondern in mehreren Schichten in entgegengesetzte Richtungen. Zudem rotieren sie nicht einfach um die y-Achse, sondern um alle Achsen gleichermassen, wodurch sie eine Kugel zu bilden scheinen. Und darüber hinaus weisen alle Partikel auch noch mit der Spitze in die korrekte Flugrichtung.

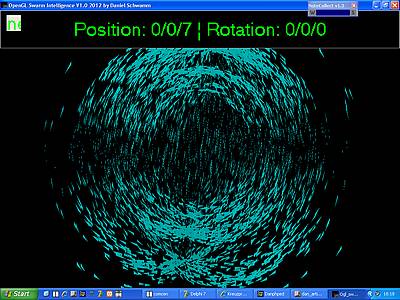
Kugelschwarm mit perfekt ausgerichteten Partikeln: Alle Partikel richten sich über alle Achsen hinweg in einem Winkel von 90 Grad auf den Mittelpunkt aus. Sie schwimmen dabei nicht synchron, sondern zum Teil in entgegengesetzte Richtungen. Die Spitze der Partikel weist stets perfekt in Flugrichtung.

Mathematisch korrekt ist das Ganze wohl nicht zu 100%, den man kann beobachten, dass sich der Kugelschwarm mit der Zeit immer mehr ausweitet. Dies wird uns aber im Weiteren nicht stören. Schöne Effekte erhält man übrigens auch, wenn man beim Richtungsvektor vor der Addition zum Positionsvektor jeweils einen Achsenwert auf null setzt; dann rotieren die Partikel nämlich röhrenförmig statt kugelförmig.

Röhrenschwarm mit perfekt ausgerichteten Partikeln: Beim Richtungsvektor der Partikel wurde die z-Achse künstlich auf null gesetzt. Dadurch rotieren die Teilchen nur noch innerhalb ihrer x-/y-Ebene und der Schwarm als Ganzes nimmt die Form einer Röhre statt einer Sphäre an.

2.9. Zusammenballung des Schwarms

2.9.1. Schwache Schwammsche Schwarm-Schwärmerei

Gestern habe ich noch etwas im Web geforscht und nirgends einen Hinweis dafür gefunden, dass meine Rotationsformel vom vorherigen Abschnitt irgendwo Anwendung findet. Nicht einmal die Idee, dass eine Kreisbahn erzwungen wird, wenn sich ein Teilchen stets in einem Winkel von 90 Grad zum Ursprung bewegt, fand ich bestätigt. Es ist also anzunehmen, dass das Ganze mathematischer Humbug ist. Ein Humbug allerdings, der so gut funktioniert, dass wir das Konzept beibehalte.

2.9.2. Eigenbewegung der Partikel zum Zentrum hin

Bereits erwähnt wurde ja, dass sich der Schwarm während der Rotation fortlaufend auszudehnen scheint. Um dem entgegenzuwirken, bauen wir nun in die Partikel eine zusätzliche Bewegung ein, die sie näher an den Ursprung führt. Auch ein echter Fischschwarm versucht ja instinktiv sein Heil in der Gruppe und verdichtet diese dadurch, weshalb überhaupt erst ein Schwarm entsteht.

Idealerweise würden sich die Partikel bei der Rotation um einen immer kleiner werdenden Radius drehen, wodurch automatisch eine Ballung im Zentrum gegeben wäre. Weil der Radius jedoch in unserer Rotationsformel nirgends so richtig vorkommt, ausser beim Positionsvektor, fand ich auch nicht die passende Schraube, an der ich drehen musste, um das Partikel näher zum Mittelpunkt zu führen. Wir lösen daher das Problem ganz billig dadurch, dass wir den Positionsvektor eines jeden Partikels permanent etwas verkürzen - theoretisch müsste sich dann der Schwarm ja früher oder später komplett in der Mitte zusammenballen. Mal schauen, ob das hinhaut!

Na, das war ja einfach. Mit nur einer Programmzeile haben wir unsere Simulation erheblich verbessern können. Und es macht grossen Spass, sich in dieses wilde Getümmel der Partikel hineinzustürzen und anschliessend all die zersplitternden, rotierenden Strukturen zu beobachten, die sich allmählich wieder im Zentrum zu treffen beginnen.

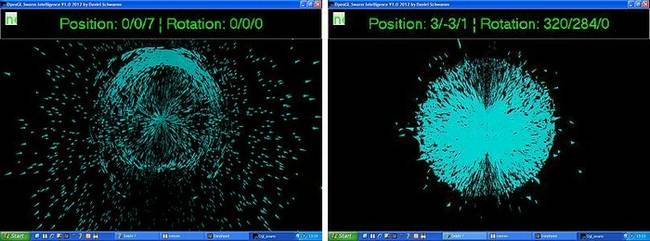
Konzentration der Partikel zum Mittelpunkt hin: Nach dem Eintauchen des Betrachters in den Schwarm weichen die Partikel zunächst explosionsartig aus. Durch Schrumpfung ihres jeweiligen Positionsvektors ballen sie sich jedoch bald wieder im Zentrum zusammen.

2.10. Auseinanderdriften des Schwarms

2.10.1. Partikelverschmelzung unerwünscht

Kritisch anzumerken ist, dass unser Schwarm aktuell nicht mehr allzu viel Ähnlichkeit mit einem Fischschwarm besitzt. Nein, der Partikelstrom wirkt nun eher wie eine Vielzahl von Elektronen, die um einen Atomkern kreisen, und dabei immer wieder verschmelzen und auseinanderplatzen. Der Grund hierfür ist - vermutlich - schon genannt: Fische sind Partikel der Makrowelt - und diese verschmelzen nicht miteinander, die beanspruchen Raum für sich selbst. Der nächste Schritt wird also sein, dieser physikalischen Gesetzmässigkeit Rechnung zu tragen.

2.10.2. Woher weiss ein Partikel die Position seiner Nachbarn?

Wie gehen wir das an? Eine Idee, die mir einfällt: Die Partikel müssen irgendwie Informationen darüber gewinnen, wo sich ihre direkten Nachbarn befinden. Kommen diese zu nahe, muss eine Ausweichbewegung initiiert werden, ähnlich wie bei der Betrachter-Detektion.

Zunächst ist der naheliegendste Weg praktisch nicht durchzuführen, aufgrund der hohen Anzahl an Partikel. Nämlich der, dass jedes Partikel vor bzw. nach der eigenen Positionsberechnung in einer Schleife den Abstand zu allen anderen Partikeln berechnet, und dem entsprechend sein Verhalten anpasst. Bei 10.000 Partikeln wären das 10.000 hoch 2, also 100.000.000 Aufrufe von "v_distance" - und das ist wohl mit keinem herkömmlichen PC in Echtzeit zu realisieren.

2.10.3. Ein Gitterraster zerteilt die Welt

Da wir nicht jeden einzelnen Punkt überprüfen können, gehen wir in gewisser Weise statistisch vor. Wir legen ein virtuelles Gitterraster über die Welt, repräsentiert durch ein dreidimensionales Integer-Array. Wenn wir nun bei der Zeichenprozedur alle Partikel durchlaufen, verteilen wir die Partikel je nach Position in eine passende Gitterbox, indem wir deren Wert um eins erhöhen. Anschliessend prüfen wir, wie viele Partikel sich bereits in der Gitterbox befinden. Überschreitet nun diese Anzahl einen gewissen Wert, dann wird das Partikel statt auf den Ursprung zu einfach von diesem wegbewegt. Dies müsste zur Folge haben, dass Partikel, die sich zu sehr zusammenballen, stets wieder voneinander gelöst werden.

2.10.4. Visualisierung des Gitterrasters

Um sich das Ganze etwas besser vorstellen, werden wir zunächst das Gitterraster in das Modell einzeichnen. Nötig sind dazu folgende Zeilen:

Die Erläuterung, wie wir die Gitterbox genau erstellen, schenken wir uns hier. Anhand der Konstanten "_raster_cell_dim" wurde festgelegt, dass jede Gitterbox eine Kantenlänge von 0.5 m hat. Insgesamt wird ein Rastergitter von 4 Kubikmetern erzeugt, d.h., es gibt insgesamt (4*2) hoch 3 = 512 Gitterboxen. Im Übrigen werden Partikel, die sich ausserhalb dieses Bereichs befinden, nicht auf eine mögliche Zusammenballung hin überprüft, denn die Wahrscheinlichkeit, dass dies gegeben ist, ist dort relativ gering.

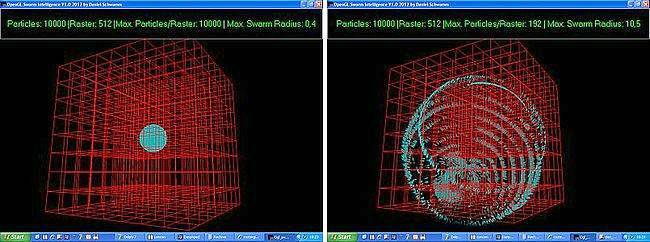
Ein Gitterraster zerteilt die Welt: Die roten Linien zeigen an, wo sich unser Gitterraster befindet. Jede sich daraus ergebende Gitterbox entspricht dem Feld eines dreidimensionalen Arrays. Die maximale Anzahl der in einer Gitterbox befindlichen Partikel wurde gezählt, ebenso der maximale Radius des Schwarms ermittelt. Im linken Bild haben sich alle 10.000 Partikel in nur einer Gitterbox zusammengeschlossen, da der Radius nur noch 0.4 m beträgt, eine Gitterbox aber eine Kantenlänge von 0.5 m besitzt. Im rechten Bild dagegen sind die Partikel deutlich verstreuter anzutreffen. In der am dichtesten verpackten Gitterbox befinden sich 'nur' noch 192 Partikel, wie man der Statusinformation im Kopf entnehmen kann.

2.10.5. Gitterboxen füllen

Wie beschrieben, besteht unser Rastergitter aus 512 Gitterboxen. Um die Dichte einer Gitterbox zu ermitteln, müssen die Koordinaten der einzelnen Partikel so umgerechnet werden, dass sie den Array-Koordinaten der zugehörigen Gitterbox entsprechen. Als Grenzwert der erlaubten Dichte legen wir den Wert 16 x 16 x 1 fest. Dies entspricht 16 Fischen mit 20 cm Länge nebeneinander, die in 16 Schichten übereinanderliegen. Da wird es bei einer Höhe von 3 cm pro Fisch schon recht eng in einer Gitterbox von 50 cm Kantenlänge.

Sehen wir uns nun an, wie wir die Füllung der Gitterboxen im Programm realisieren können:

In der Prozedur "draw_scene" wird "draw_particles" aufgerufen. Dort wird das komplette Array "raster_a" mit null vorbelegt. Anschliessend werden die Partikel gezeichnet und danach eine Statistik auf dem Bildschirm ausgegeben, z.B. der grössten ermittelte Wert der Dichte (Partikel/Raster).

In der Prozedur "calc_position" von TParticle wird der Abstand des Partikels zum Mittelpunkt ermittelt. Danach wird mithilfe dieses Wertes geprüft, ob wir uns innerhalb des Rastergitters befinden. Ist dies der Fall, rechnen wir die Pixel-Koordinaten in Array-Indizes um, indem wir die Fliesskommazahlen der Positionskoordinaten durch die Grösse einer Rasterbox teilen und anschliessend die Nachkommastellen verwerfen.

Sehen wir uns das an einmal einem Beispiel an:

Die ermittelte Rasterbox wird um 1 erhöht. Überschreitet ihr Wert die maximal zulässige Dichte - hier 16*16*1 Partikel - dann wird die Dichte-Flucht initiiert. Dies bedeutet einfach, dass der aktuelle Positionsfaktor skaliert mit einem Wert grösser 1 zum neuen Positionsvektor wird. Der Vektor wird also nur etwas verlängert, wodurch die Partikel sich vom Zentrum wegbewegen.

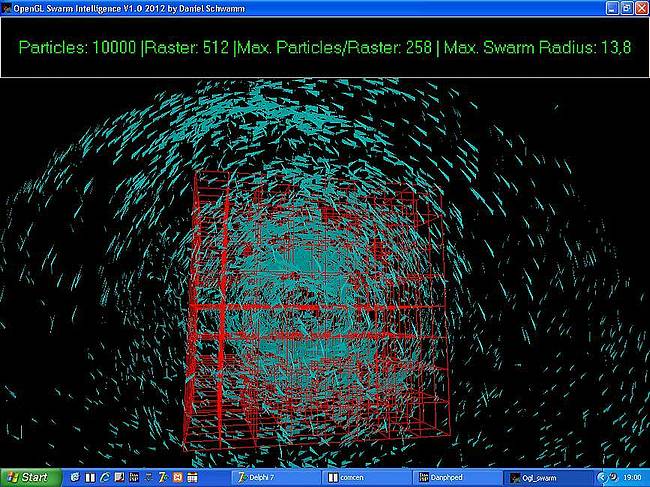
Schwarm mit verteilter Dichte: Noch immer bewegen sich unsere Partikel um das Zentrum herum und gleichzeitig auch auf das Zentrum zu. Wird jetzt jedoch in einer Gitterbox eine zu hohe Dichte an Partikeln festgestellt, so bewegen sich diese auf zufällige Weise wieder nach aussen. Dadurch wird eine 'unnatürliche' Zusammenballung der Partikel erfolgreich verhindert.

3. End of Holiday oder: Ein Sprung in der Entwicklung

Bis hierher war ich innerhalb meines Eine-Woche-Urlaubs gekommen. Zu diesem Zeitpunkt war ich schon recht zufrieden mit meinem Schwarm und wollte zunächst auch gar nicht mehr weiter daran herumbasteln. Dieser Vorsatz fiel aber schnell in sich zusammen, als ich bereits zwei Tage später nach Dienstschluss nichts Rechtes mit mir anzufangen wusste. Also spuckte ich in die Hände und liess erneut meine flinken Fingerchen Samba tanzen auf der Tastatur.

Das Programmieren ging mir dabei gut von der Hand und der Schwarm wurde noch sehr stark verbessert. Leider fehlte mir allerdings die Energie, dieses Tutorial wie bisher parallel zur Entwicklung fortzuschreiben. Aus diesem Grund beschränken wir uns im Folgenden damit, einige der Verbesserungen, die den "Evolutionsprozess" überlebt haben, zu erläutern. All die Irrwege, die ich zwischenzeitlich verfolgte und die teilweise durchaus interessante Ansätze enthielten, bleiben also leider aussen vor.

3.1. Trägheit eines Partikels

Wie wir gesehen haben, wird zu jedem Partikel eine neue Richtung berechnet, die dann zum Positionsvektor dazu addiert wird. Eine leicht zu realisierende Möglichkeit war es, hier den Partikeln einen Trägheitszähler zu geben, der per Zufall auf einen bestimmten Zahlenwert gesetzt wird. Bei jedem Draw-Ereignis wird der Trägheitszähler dekrementiert. Solange er grösser als Null ist, findet keine Neuberechnung der Richtung statt. Dadurch bleibt die alte Richtung bestehen und unser Teilchen verhält sich gewissermassen träge. Und das bringt ganz nette optische Effekte mit sich.

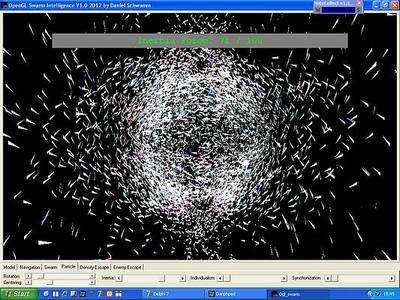
Trägheit von Partikeln: Auf dem Standbild ist es natürlich nur schwer zu erkennen, aber alle weiss gefärbten Partikel auf diesem Bild verhalten sich träge. D.h., sie behalten die einmal ermittelte Richtung für eine zufällige Zeitdauer bei. Dadurch wird die bisherige etwas stupide Kreisbewegung der Partikel aufgebrochen, da sie nun ab und an auch einmal eine Gerade fliegen.

3.2. Individualismus eines Partikels

An verschiedenen Stellen arbeiten wir bei der Berechnung der Richtung eines Partikels mit Zufallswerten. Die Berücksichtigung dieser Zufallswerte wird ab sofort mithilfe eines optionalen Wertes der Individualität bestimmt. Dabei gilt, dass auf Zufallswerte so weit als möglich verzichtet wird, wenn die Individualität auf null steht. Die exakt berechnete Werte werden im Gegensatz dazu umso weniger berücksichtigt, je höher der Grad der Individualität eingestellt wird. So kann man mit nur einem zentralen Regler recht genau den Grad an Chaos im Schwarm in der gewünschten Weise variieren.

Hier sind nur zwei Stellen exemplarisch genannt, die auf unsere Zufallsfunktionen zurückgreifen. "get_particle_random" liefert einen Wert zurück, der maximal "v" betragen kann, aber je weniger Individualität vorgegeben ist, umso kleiner fällt der Rückgabewert aus. ""get_particle_invers_random" verhält sich genau umgekehrt. Je grösser die Individualität, umso kleiner wird das Ergebnis.

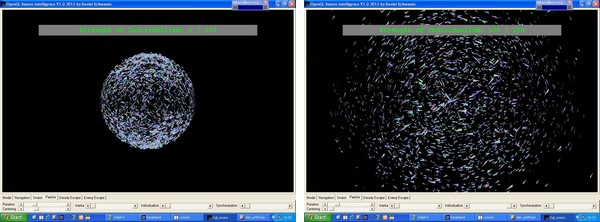
Individualismus eines Partikels: Im linken Bild wurde der Individualismus der Partikel auf null gesetzt - alle Partikel ordnen sich brav zu einer Kugelformation an. Im zweiten Bild hingegen haben wir 100% Individualismus. Die Teilchen halten sich kaum mehr an Regeln und erkunden in chaotischer Formation ihr Umfeld.

3.3. Weiche Richtungsänderungen

Bei jedem Draw-Ereignis wird für alle Partikel eine neue Richtung ermittelt (sofern sie nicht gerade träge sind). Um hierbei zu abrupten - und damit unnatürlichen - Richtungsänderungen vorzubeugen, wird die neue Richtung dergestalt berechnet, dass dabei bis zu einem gewissen Grad auch die alte Richtung mit berücksichtigt wird. Dadurch fliegen die Partikel in deutlich sanfteren Kurven und schlagen nur noch selten plötzliche Haken.

Zu Beginn wird die alte Position in "old_dir_v" gesichert. Dann erfolgt die Berechnung der neuen Richtung in "dir_v". Am Schluss wird mit "d" ein Zufallswert zwischen 0 und 1 ermittelt. Die alte Richtung wird mit "d" skaliert, die neue Richtung mit 1-d. Anschliessend wird durch Vektoraddition ein Mittelwert aus beiden Vektoren berechnet, der die neue Richtung vorgibt. Durch den Zufallsfaktor "d" kann es unter Umständen auch passieren, dass ein Partikel seine Richtung überhaupt nicht ändert - oder aber doch wie zuvor schon in abrupter Weise. Alles ist möglich, alles ist erlaubt.

3.4. Verbesserte Dichteflucht

3.4.1. Dichteflucht als Einflussgrösse für den Richtungswechsel

Bisher sind wir bei der Dichteflucht so vorgegangen, dass einfach ein verlängerter Positionsvektor zurückgeliefert wurde, der das Partikel wieder nach aussen treibt. Dabei gingen jedoch alle zuvor berechneten Richtungsänderungen verloren, wodurch sich ein etwas statisches Bild der fliehenden Partikel ergab. Nun berechnen wir aus dem Positionsvektor einen Richtungsvektor und liefern diese zurück, wobei dieser Richtungsvektor Einfluss nimmt auf den endgültigen Richtungsvektor, in den auch Rotation, Zentralisation und Feindesflucht einfliessen.

3.4.2. Beschleunigung und Abbremsung

Ähnlich wie bei der Trägheit wird auch bei der Dichteflucht ein Zähler gesetzt, der dafür sorgt, dass die Fluchtrichtung eine Weile eingehalten wird. Um den Verlauf der gesamten Fluchtbewegung etwas natürlicher zu gestalten, steigert das Partikel zunächst sein Tempo und bremst dann ab der Mitte allmählich wieder ab.

3.4.3. Mehr Volumen bei der Flucht

Die Praxis hat gezeigt, dass bei einer Verflachung des Schwarms die Dichteflucht dafür sorgt, dass sich die Teilchen nur innerhalb der rotierenden Schwarmscheibe nach aussen bewegen, da dies der schnellste Weg ist, sich vom Mittelpunkt zu entfernen. Ein kleiner Korrekturterm sorgt dafür, dass bei dieser Flucht auch in die jeweils vernachlässigte dritte Dimension vorgestossen wird; der fliehende Schwarm bekommt dadurch mehr Volumen verpasst und sieht damit natürlicher aus. Übrigens gilt hierbei: Je höher der Grad an Individualität, umso stärker fällt die Fluchtbewegung aus dem Scheibenverband aus.

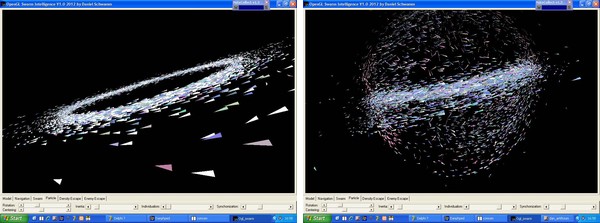
Verbesserte Dichteflucht: Im linken Bild haben die Partikel wenig Individualität und neigen unter gewissen Umständen zur Scheibenbildung. Kommt es dabei zu hohen Dichteverhältnissen in den Gitterboxen, dann fliehen die Partikel derart nach aussen, dass die Scheibe vergrössert wird. Beim rechten Bild haben wir es dagegen mit individuellen Partikeln zu tun, die auch weniger optimale Fluchtwege in Betracht ziehen. Bei Verdichtungen springen diese geradezu heraus aus der Scheibe - und erinnern damit einmal mehr an natürliche Fischschwärme. Die Dauer und die Geschwindigkeit der Fluchtbewegung lassen sich jetzt zudem über Parameter beeinflussen.

3.5. Statt nur Beobachterflucht erweiterte Feindesflucht

Wie weiter oben implementiert, verfügen unsere Partikel über einen "angeborenen" Fluchtmechanismus, wenn man sich ihnen zu sehr nähert. Sie fliehen dann explosionsartig davon, und zwar so, dass sie möglichst effektiv dem potenziellen Angreifer entkommen können.

Leider musste man bisher als Betrachter der Szenerie zuerst in den Schwarm hineintauchen und dann sofort wieder (rückwärts) herausfliegen, damit man von dem schönen Schauspiel auch etwas mitbekommen konnte. Und so entstand der Wunsch, dass man aus einiger Entfernung Bomben auf den Schwarm abschiessen kann. Dann könnte man in aller Ruhe die Reaktion geniessen. Ja, durch mehrfaches, gezieltes Schiessen könnte man dann sogar die Formation des Schwarms in gewünschter Weise abändern.

3.5.1. Anleitung zum Bombenbau

Also mussten ein paar Bomben her. Etwas Erfahrung damit habe ich ja schon bei "OpenGL ISS" sammeln können: Kapitel 3.9.2. von "OpenGL ISS" - Meteor-Handling.

Wir beschränken uns auf 10 Bomben, deren Eckdaten jeweils in einem Record "TBullet" gesichert werden. Wie auch der Fischschwarm werden die Bomben mittels eines Arrays verwaltet. Anders als bei den Partikeln verwenden wir für die Bomben jedoch OpenGL-Objekte, die wir mit einer Textur versehen. Aufgrund ihrer geringen Anzahl dürfte dies kaum ein Problem mit der Performance mit sich bringen.

In "FormCreate" wird "bullet_tx" mit der Textur des Bildes "bullet_img" verknüpft. Anschliessend wird das TBullet-Array in einer Schleife mit Werten gefüllt, wobei jeweils die Textur-Eigenschaft aktiviert wird.

In "FormDestroy" wird das TBullet-Array wieder sauber eliminiert.

In "model_frequency_tTimer" wird geprüft, ob die Leertaste betätigt wurde. Wenn ja, wird in einer Schleife nach der ersten freien Instanz des TBullet-Arrays gesucht. Wird eine solche Instanz gefunden, wird die Schussrichtung "dir_v" auf den letzten "my_look_vector_get"-Vektor gesetzt, der ja exakt in die Richtung zeigt, in die der Benutzer in unsere virtuelle Welt hineinschaut. Anhand von "bullet_a[r].count" kann dann später festgestellt werden, ob diese Bombe gerade unterwegs zu ihrem anvisierten Ziel ist.

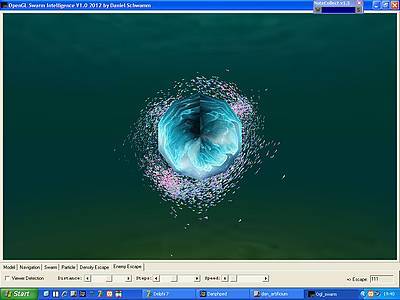
Bombe auf ihrem Weg zum Schwarm: Der Benutzer hat die Leertaste betätigt und damit eine Bombe auf ihren Weg zum Schwarm geschickt. In wenigen Sekunden wird sie dort mitten hineinbrechen und den Schwarm gehörig in Aufregung versetzten. Um die Verwirrung noch mehr zu steigern, können sogar bis zu 10 Bomben gleichzeitig abgeschossen werden!

3.5.2. Die erweiterte Feindesflucht

Natürlich müssen wir unsere bisherige Viewer-Escape-Routine nun so erweitern, dass sie nicht nur auf die Nähe des Betrachters reagiert und eine Fluchtbewegung des Partikels initiiert, sondern dies auch macht, wenn sich eine Bombe im Gefahrenbereich befindet.

Wir befinden uns in Prozedur"calc_pos". Wir haben die Rotation, die Zentralisation und die Dichteflucht-Richtung zu einer neuen Richtung gemittelt. Nun wird geprüft, ob sich unser Partikel im Gefahrenbereich von Feinden befindet.

Zunächst überprüfen wir dies bezüglich des Betrachters. Dazu berechnen wir in "distance" den Abstand des aktuellen Partikels zum Betrachter. Diesen Wert übergeben wir dann an die Funktion "get_enemy_escape_v".

In ganz ähnlicher Weise verfahren wir direkt im Anschluss mit den Bomben, die wir in einer Schleife durchlaufen. Zunächst wird geprüft, ob die Bombe überhaupt abgeschossen wurde (ihr interner Zähler ist dann grösser null). Ist dem so, wird wie beim Betrachter "distance" berechnet, jetzt natürlich auf die Bombe bezogen, und an "get_enemy_escape_v" übergeben. In allen Fällen erhalten wir einen neuen Richtungsvektor zurück (einen Null-Vektor, wenn keine Gefahr besteht), der zum bereits bestehenden Richtungsvektor dazu addiert wird.

In der Funktion "get_enemy_escape_v" wird überprüft, ob der übergebene "distance"-Wert im kritischen Bereich ist. Ist dem so, wird die Fluchtbewegung initiiert. Der neue Richtungsvektor wird dabei so gewählt, dass sich unser Partikel in direkter Linie vom Feind entfernt. Wir erhalten diesen gesuchten Vektor, indem wir einfach die Position des Feindes von der Position des Partikels abziehen. Danach folgt noch etwas Programmierer-Mystik mit der Geschwindigkeit und einige Variationen mit Zufallswerten, damit die Fluchtrichtung nicht zu einheitlich wird.

Des Weiteren wird festgestellt, ob wir uns in der Endphase der Flucht befinden. Ist dem so, entfernt sich das Partikel nämlich nicht weiter vor seinem Feind, sondern steuert vielmehr wieder auf den für das Partikel sichersten Ort zu - das Zentrum des Schwarms.

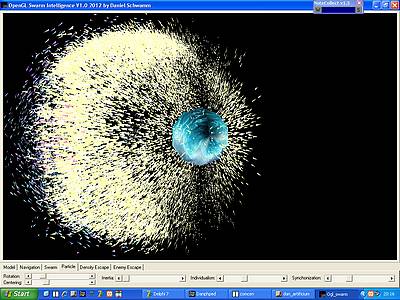
Schwarm flieht vor Bombe: Eine Bombe bewegte sich seitlich am Schwarm vorbei. Dies hatte zur Folge, dass die rechtsseitigen Partikel nach links geflohen sind. Je näher sie an der Bombe dran waren, umso schneller sind sie auseinandergestoben. Dadurch wirkt es nun so, als sei seitlich des Schwarms eine gewaltige Explosion erfolgt. Alle fliehenden Partikel sind gelb markiert.

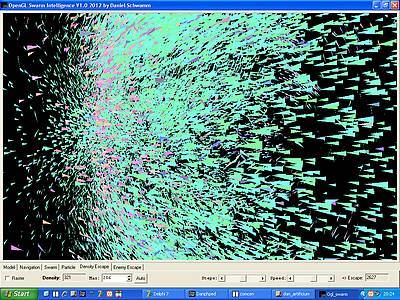
Partikel fliehen in den Schwarm: Nachdem die Partikel in der ersten Phase der Flucht in entgegengesetzter Richtung zu ihrem Feind flohen, kehren sie in der zweiten Phase verstärkt in die Sicherheit des Schwarms zurück. Man kann dies z.B. ausnutzen, indem man um die Ränder des Schwarms Bomben verteilt, wodurch sich die Partikel mit der Zeit immer mehr zu einem dichten Schwarm zusammenballen. Alle zurückkehrenden Partikel sind grün markiert.

3.6. Kolorierung der Partikel

Um (als Programmierer) abschätzen zu können, was die hauptsächliche Motivation eines Partikel für seine aktuelle Richtung ist, lassen sich diese optional eingefärbt. Alle Partikel bekommen bei ihrer Erzeugung zunächst einen Farbwert zugeordnet, der einem Blauton entspricht - dies erschien mir nämlich für Fische als am geeignetsten. Partikel, die eine träge Bewegung ausführen, werden dagegen weiss wiedergegeben. Partikel wiederum, die aufgrund zu hoher Dichte aus dem Schwarm entfliehen, werden rot markiert. Durch äussere Feinde aufgeschreckte Partikel sind panisch gelb - und sowie sie sich wieder etwas beruhigt haben und zum Schwarm zurückkehren, werden sie gemütlich grün gemalt. Wenn sie sich dann wieder in einem neutralen Zustand befinden, nehmen sie erneut ihre originale Blaufärbung an. Da diese Umfärbung für Fische eher untypisch ist, kann diese Option selbstverständlich auch wieder deaktiviert werden.

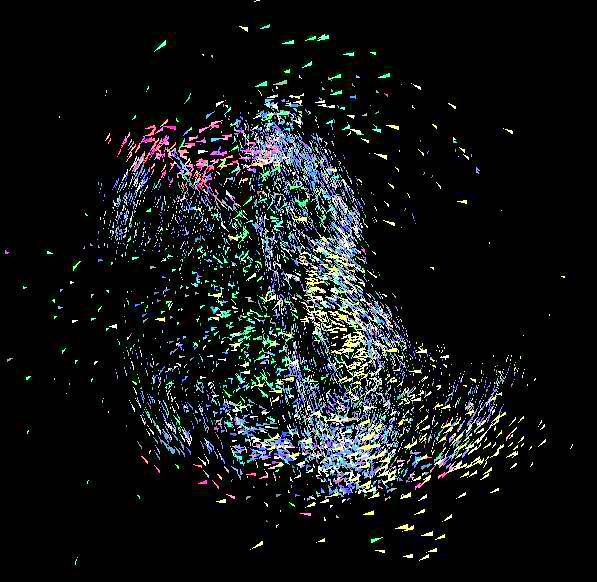
Umfärbung der Partikel: Bei obigem Bild haben wir alle Farbstufen beisammen. Am rechten Rand überwiegen die blauen Fische im Normalzustand. Dazwischen gibt es immer wieder auch weisse Fische, die gerade eine träge Bewegung ausführen, ihre aktuelle Richtung als für eine Weile beibehalten. Die gelben Fische unten links sind auf der Flucht vor einer Bombe, während die grünen Fische in der Mitte die Sicherheit des Zentrums des Schwarms anstreben. Und ganz oben links sieht man einige rote Partikel - diese entfliehen gerade einer zu sehr verdichteten Zone im Schwarm.

3.7. Synchronisierung der Partikel

Ein besonderes Schmankerl habe ich erst sehr spät in den Schwarm einbauen können: Synchronisation. Lange Zeit fehlte mir nämlich die rechte Idee, wie ich es umsetzen könnte, dass die Partikel die Neigung entwickeln, sich auch an der eingeschlagenen Richtung ihrer Nachbarn zu orientieren. Denn wie schon bei der Dichte-Ermittlung erfahren, ist es schlicht nicht möglich, die Positionen alle Nachbarn eines Partikels permanent zu ermitteln, zumindest nicht in vertretbarer Zeit.

Daher verfahren wir jetzt ähnlich wie bei der Berechnung der Dichte: Wir holen uns die Richtungsvektoren aller Partikel einer Rasterbox und summiere diese zu einem gemittelten Gesamtvektor auf. Danach muss ein Partikel nur noch in seiner Rasterbox den entsprechenden Richtungsvektor entnehmen und davon seine eigene Richtung bis zu einem gewissen Grad beeinflussen lassen. Und schon haben wir eine Angleichung der Bewegungen der Partikel erreicht. Im Nachhinein weiss ich eigentlich auch nicht mehr, warum es mit der Umsetzung so lange nicht klappen wollte.

Über das sagenhafte Ergebnis dieses Verfahrens war ich jedenfalls selbst äusserst positiv überrascht. Bisher neigte unser Schwarm nämlich stets dazu, entweder flache Scheiben oder aber kugelrunde Blasen zu bilden. Durch die Synchronisation der Partikeln mit der gemittelten Richtung der zugehörigen Rasterbox kamen aber auf einmal sehr schöne und abwechslungsreiche Muster zustande, die sich permanent ändern und manchmal abrupt die Richtung ändern, was dem Schwarm letztendlich doch noch ein sehr natürliches Aussehen verleiht, wie ich finde.

Während uns vorher für die Dichte ein einfaches mehrdimensionales Array mit Integer-Werten genügte, müssen wir nun einen Record "TDensity" damit verwalten. Denn neben der Anzahl der Teilchen einer Rasterbox müssen wir uns nun auch die Durchschnittsrichtung all dieser Teilchen merken.

Fangen wir unten bei "draw_scene" an. Dort wird die interne Prozedur "draw_particle" aufgerufen. In dieser mussten wir bisher auch schon das Raster-Array durchlaufen und die Zähler auf null setzen. Nun löschen wir bei dieser Gelegenheit auch noch gleich den neu dazugekommenen Richtungsvektor mit. Die Schleife zur Ausgabe der Partikel kehrt sich im Gegensatz zu früher periodisch um. Der Grund dafür liegt darin, dass nicht immer nur die Richtungen der ersten paar Partikel die Durchschnittsrichtung der zugehörigen Rasterbox dominieren sollen. Idealerweise hätte man wohl die Partikel in zufälliger Reihenfolge ausgegeben, doch meine Versuche in dieser Richtung schluckten zu viel Zeit. Indem wie jetzt die Reihenfolge einfach nur ständig umgekehrt wird, kommt aber ebenfalls ein mehr als hinreichendes Ergebnis zustande.

In Prozedur "TParticle.calc_pos" wird in gewohnter Weise die Richtung der Dichteflucht ermittelt. Gleichzeitig werden aber auch die Koordinaten der zugehörigen Rasterbox zurückgeliefert, sondern das Partikel sich innerhalb einer solchen befindet. Nun muss nur noch der gemittelte Richtungsvektor der Rasterbox genommen werden und mit einem Zufallswert durch Vektoraddition Einfluss auf den bisher ermittelten Richtungsvektor nehmen.

Übrig bleibt noch die Füllung der Rasterbox mit der Durchschnittsrichtung. Dies geschieht in Prozedur "get_density_escape_v". Wurde hier festgestellt, dass sich das Partikel innerhalb einer Rasterbox befindet, wird nun der aktuelle Richtungsvektor zum Richtungsvektor der Rasterbox dazu addiert. Bei den ersten Partikeln ist der so generierte Richtungsvektor eigentlich noch wenig aussagekräftig, aber das ändert sich sehr schnell. Diejenigen Partikel, die sich am anfänglichen Richtungsvektor orientieren, sind dann halt Ausreisser, aber von denen gibt es in der Natur ja auch immer ein paar.

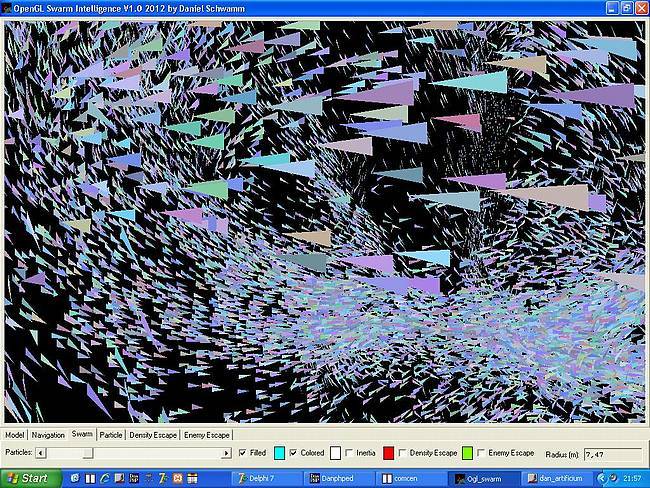
Synchronisierung 1 - Partikel-Stränge im Schwarm: Je nachdem, durch welche Rasterbox die Partikel laufen, verbinden sie sich mit ihren direkten Nachbarn zu verdichteten Schwärmen innerhalb des Gesamtschwarms. Einige dieser Stränge sind sehr dick, während andere bisweilen nur ein Partikel nach dem anderen aufweisen.

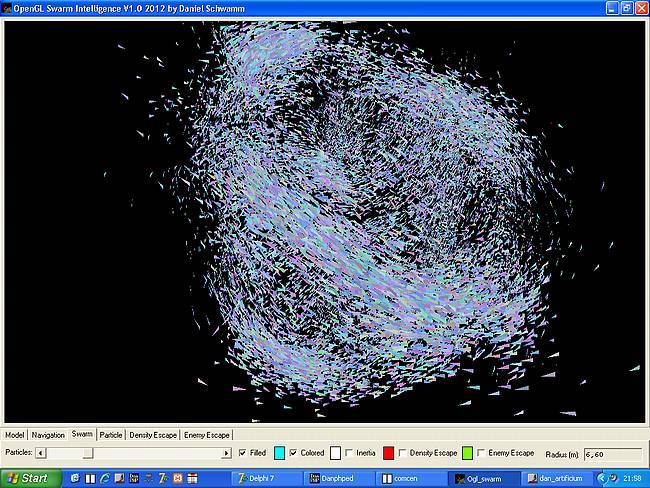
Synchronisierung 2 - dreidimensionale Schleifen: Ein chaotisch verwirbelter Schwarm wird durch äussere Einflüsse in seiner Struktur verändert. Rotation und Zentralisierung, aber auch Dichte- und Feindesflucht sorge so immer wieder dafür, das sich bestimmte Richtungen durchsetzten, und dadurch im Schwarm pulsierende Ströme aus Partikeln entstehen, die sich gegenseitig synchronisieren.

Synchronisierung 3 - Brücken und Wirbel: An Kreuzstellen verdichteter und synchronisierter Stränge kommt es oft zu spontanen Richtungsänderungen der Partikel, da hier keine Richtung dominiert. Dann treten plötzliche geradlinige Bewegungen auf und die Partikel schiessen mitten durch das Zentrum des Schwarms, um sich mit dem Strom der Partikel auf der anderen Seite zu verbinden. Manchmal wirbeln sie auch aus dem Schwarm heraus, durchlaufen eine Schleife und tauchen dann wieder in den Hauptschwarm hinein. Eine derartig angelegte Bahn wird mit der Zeit immer dominanter, bis es vielleicht zu einer Kollision mit einem anderen anwachsenden Strang kommt - und alle Wege wieder offen sind.

4. Fazit

Als wir mit unserem Projekt begonnen haben, das Verhalten eines Schwarms zu simulieren, wussten wir nicht, ob und wie sich das Ziel erreichen lässt. Wie fängt man so etwas an? Wie kann man zig tausend Individuen steuern? Und wie kann man das Ganze dann auch noch grafisch reizvoll wiedergeben?

Wie so oft (bei der Programmierung) half uns hier eine simple Lebensweisheit, die die folgende Frage beantwortet: "Wie ist man einen Elefanten?" Einen Bissen nach dem anderen!

Zunächst schufen wir einen virtuellen Raum für den Schwarm mithilfe von OpenGL. Wir generierten erste, kugelförmige Partikel, die wir in diesem Raum zufällig verteilten, und die dort unbeweglich stehen blieben. Die Implementierung einer Steuerung setzte uns in die Lage, diese Partikel aus allen Richtungen zu betrachten. Als nächste Massnahmen liessen wir die Partikel auf die Nähe des Betrachters reagieren, indem wir diese von ihrem "Feind" zurückweichen lassen. Das Aussehen der Partikel wurde variiert - sie wurden von Kugeln zu Dreiecken. Dreiecke besitzen jedoch eine Richtung, weshalb wir das vielleicht grösste Problem des Projekts zu lösen hatten, nämlich die Partikel stets in ihre Bewegungsrichtung blicken zu lassen. Auch die Rotation war eine harte Nass, die jedoch ohne Verwendung von komplizierten Formeln, alleine durch wenige Vektoroperationen realisiert werden konnte. Der Rest - die Zentrierung, die Dichteflucht, die Bomben, die Feindesflucht und sogar die zuletzt eingebaute Synchronisation der Partikel - all das war dann vergleichsweise einfach umzusetzen.

Das Ergebnis mag nicht perfekt sein. So stört mich, dass die Partikel sich stets nur am Ursprung des Modells orientieren. Echte Fische kennen aber keinen Ursprung. Die Vermutung liegt nahe, dass diese sich ihren Mittelpunkt ständig neu suchen, und zwar vermutlich dort, wo das jeweilige Zentrum ihres (lokalen) Schwarms liegt, d.h. die dichteste Stelle, die sie optisch erfassen können.

So etwas verdirbt mir jedenfalls nicht den Spass an meinem Proggy. Ist halt nichts 100%iges. But who cares?

5. Video-Demonstrationen von "OpenGL-Swarm" bei YouTube

6. Download

"OpenGL Swarm" wurde in Delphi 7 programmiert. Im ZIP-File enthalten ist der vollständige Source-Code, die OpenGL-Unit "dglOpenGL.pas", die OpenGL-DLL "opengl32" sowie die EXE-Datei. Das Paket, etwa 760 kB, gibt es hier:

OpenGL-Swarm.zip

Have fun!