Diplomarbeit - Konstruktion von NN für Regressionsanalysen - Anhang
von Daniel Schwamm (09.11.2000)
ANHANG
ANHANG A: Zwei Projekte des Zentrums für Europäische Wirtschaftsforschung
Projekt A
-
Insolvenzanalysen mit Neuronalen Netzwerken
-
Projektleiter:
-
Prof. Dr. Dr. h.c. Heinz König
-
Projektbearbeiter:
-
Dipl.-Wirtsch.-Inf. Andrea Szczesny
-
Dipl.-Stat. Olaf Korn
-
Dipl.-Wirtsch.-Ing. Ulrich Anders
-
Dr. Martin Kukuk
-
Aufgabenstellung:
Die Gesamtzahl der Insolvenzen ist in den vergangenen Jahren stark angestiegen.
Ein Ende dieser Entwicklung ist noch nicht abzusehen. Die lange Talfahrt der
zurückliegenden Rezession hat die Unternehmen ausgezehrt. Banken sind bei
der Kreditvergabe vorsichtiger geworden. Gerade kleine und
mittelständische Unternehmen brauchen jedoch Unterstützung durch
Kreditinstitute. Für die Zukunft ist es daher wünschenswert,
Analyseverfahren zu entwickeln, die eine kundenindividuelle Bewertung von
Kreditrisiken ermöglichen. Fast alle Kreditinstitute, der Deutsche
Sparkassen- und Giroverband setzen seit mehreren Jahren statistische Verfahren
zur Einschätzung des Kreditrisikos ein, unter anderem lineare Regressions-
und Diskriminanzanalyseverfahren. Neben diesen klassischen Verfahren bieten
sich neuere quantitative Methoden wie der Einsatz Neuronaler Netzwerke an.
Das Forschungsprojekt gliedert sich in zwei Bereiche. Zum einen werden
verschiedene Verfahren zur Kreditwürdigkeitsanalyse gegenübergestellt
und bewertet. Ein Schwerpunkt liegt dabei auf moderneren Verfahren der
wissenschaftlichen Literatur. Im Rahmen einer empirischen Analyse soll zum
anderen ein System entwickelt werden, das den Anforderungen der Praxis gerecht
wird und sich gut für Prognosen von Insolvenzen und Kreditausfallrisiken
eignet. Die im Forschungsbereich Industrieökonomik und Internationale
Unternehmensführung gesammelten und aufbereiteten Daten des VCC bilden
hierfür die vielversprechende Analysebasis.
-
Laufzeit:
-
April 1995 - November 1996
Projekt B
-
Einsatz künstlicher Neuronaler Netzwerke im Finanzbereich
-
Projektleiter:
-
Prof. Dr. Dr. h.c. Heinz König
-
Projektbearbeiter:
-
Dipl.-Wirtsch.-Ing. Ulrich Anders
-
Dipl.-Wirtsch.-Inf. Andrea Szczesny
-
Aufgabenstellung:
Neuronale Netzwerke sind eine leistungsfähige und flexible Klasse von
statistischen Verfahren in der Ökonometrie. Neuronale Netzwerke sind
parametrische Verfahren. Der wesentliche Unterschied zu herkömmlichen
parametrischen Verfahren besteht darin, dass sie keine Annahmen über
die funktionale Form des zu approximierenden Zusammenhangs benötigen. Der
Einsatz von Neuronalen Netzwerken bietet sich gerade deshalb bei
ökonomischen Fragestellungen an, da in der Regel dort die
Wirkungszusammenhänge zwischen den ökonomischen Grösse ex
ante nicht bekannt sind. Neuronale Netzwerke lassen sich darüber hinaus
auch als nichtparametrische Verfahren interpretieren, die in den letzten Jahren
in der wissenschaftlichen Literatur verstärkt Beachtung gefunden haben.
Das Projekt beschäftigt sich in methodischer Hinsicht mit dem
Modellbildungsprozess beim Einsatz Neuronaler Netzwerke unter einer
ökonomischen Perspektive. Die iterative Vorgehensweise bei der
Modellierung mit Neuronalen Netzwerken unterteilt sich dabei in vier Schritte:
Identifikation der Daten, Spezifikation des Modells, Schätzung der
Parameter und Diagnose des Modells. Die Iteration dieser Schritte soll erst
abgebrochen werden, wenn die Diagnose des Modells zufriedenstellend ist.
Die gewonnen methodischen Erkenntnisse sollen für die Erklärung und
Prognose von Finanzmarktdaten sowie zur Analyse der Preisbildung von
Finanzderivaten am Markt mittels Neuronaler Netzwerke zum Einsatz kommen.
-
Laufzeit:
ANHANG B: Vorteile nichtlinearer Regressionen gegenüber linearen Regressionen
Betrachtet werden die univariaten Zeitreihen (Variablen) mit 50 Beobachtungen
x = {0.02, 0.04, 0.06, ..., 0.98, 1},
y = x2.
Eine lineare Einfachregression regressiert y auf x folgendermassen:
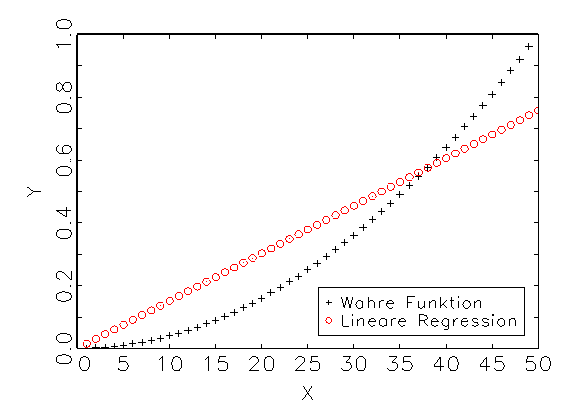
Die Regressionsfunktion ist - bedingt durch nur eine Eingabevariable - eine
Gerade, die die "Natur" der wahren Funktion nicht abbilden kann. Um
die Nichtlinearität von y zu erklären, wird über Neurometricus
ein neuronales Netzwerk generiert, welches ein Eingabeneuron, ein verstecktes
Neuron und ein Ausgabeneuron enthält. Dadurch ergibt sich folgendes
Resultat:
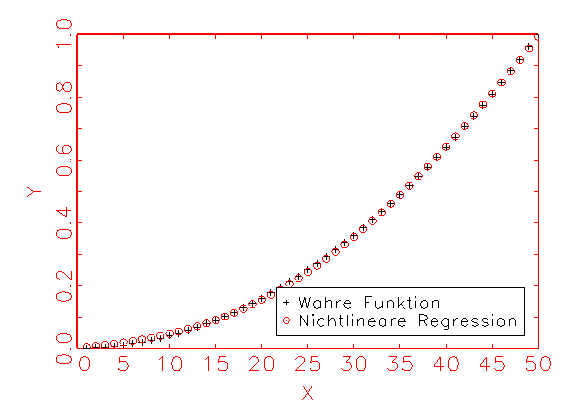
In diesem Fall gibt die Regressionsfunktion die quadratische "Natur"
der wahren Funktion korrekt wieder. Bias und Varianz fallen dadurch erheblich
kleiner aus, als beim linearen Regressionsmodell. Untenstehende Tabelle gibt
das grafisch gezeigte Ergebnis in metrischer Form wieder. Als
Gütemass für die Schätzung des Modells wurde dabei das in
der Statistik übliche R2-Kriterium herangezogen.
| |
Güte |
Varianz |
| Lineare Regression |
0.85764 |
0.013394 |
| Nichtlineare Regression |
0.99977 |
0.0000223 |
ANHANG C: Mathematik der Regressionsmodelle und neuronalen Netzwerke
Sei X die Menge von i unabhängigen Variablen, y die
Menge der abhängigen Variable und t die Anzahl der Beobachtungen je
Variable von X und y. Die vermutete funktionale Beziehung
zwischen X und y lässt sich dann in Matrixnotation
folgermassen formulieren:
y = F(X)+e,
wobei F die gesuchte Regression darstellt und e
einen Störterm repräsentiert, der per (später zu
überprüfenden) Annahmen einen Erwartungswert E[e
|X]=0, sowie eine unabhängig von X seiende Normalverteilung
besitzt. F wird auch wahre Funktion genannt. Ziel ist es, eine
Funktion f(wh,X) zu finden, die die wahre Funktion F
möglichst genau approximiert. Der Verlauf der Approximationsfunktion wird
dabei massgeblich durch die Modellparameter wh bestimmt, wodurch
sich das Problem auf die Suche der wahren/optimalen Parameter w für
wh reduziert.
Man betrachte nun folgendes einfaches lineares Regressionsmodell:
y = X×w+e
mit den Annahmen:
E[e]=0
E[e
e
‘]=s
2×
I (Homoskedastizität).
Dieses lineare Regressionsmodell lässt sich über Neurometricus
als neuronales Netzwerk implementieren, indem nur i Alpha-Gewichte
allokiert werden. Für den Ist-Output, den die Netzwerkfunktion (nach der
Schätzung der wahren Parameter w) für (wh,X) liefert,
gilt dann:
yh = f(wh,X) = S
(Alphagewichte×X).
Das zugehörige, durch die Schätzung von wh zu minimierende
Zielkriterium des Mean Squared Errors berechnet sich durch
MSE = (1/t)×
S
(y-f(wh,X))2
Durch Zerlegung des MSE erhält man
MSE = E[(y-f(wh,X))2]
= E[(y-F(X)+F(X)-f(wh,X))2]
= E[(y-F(X))2]+E[(F(X)-f(wh,X))2]+
2E[(y-F(X))(F(X)-f(wh,X))]
= E[(y-F(X))2]+E[(F(X)-f(wh,X))2]+0
= MSEu+MSEs
den systematischen und unsystematischen MSE, wobei
MSEu=e
entsprechen sollte, also durch kein Modell erklärbar ist. Der
MSEs lässt sich dagegen weiter aufteilen in
MSEs = Bias[f(wh,X)]2+Var[f(wh,X)],
da er als Punktschätzer des MSE interpretiert werden kann.
Über diesen mathematischen Zusammenhang kann das in der Arbeit
beschriebene Bias-Varianz-Dilemma begründet werden, zumal allgemein
für Punktschätzer gilt:
Bias[wh] = E[wh]-w
Var[wh] = (1/t)×(wh-E[wh])2,
woraus ersichtlich wird, dass der Bias mit steigendem Freiheitsgrad sinkt,
die Varianz dagegen wächst.
Das Zielkriterium der Maximum-Likelihood-Methode zur Bestimmung der optimalen
Parameter wh basiert ebenfalls auf dem MSE, sofern normalverteilte
Residuen vorausgesetzt werden können. Das lässt sich
folgermassen zeigen:
Sei eine Menge von Beoabachtungen
(x1,x2,...,xT) gegeben, die
unabhängig voneinander gemäss der gemeinsamen
Wahrscheinlichkeitsverteilung P(X|w) der Zufallsvariable X
gezogen wurden. Dann wird die Verteilung der Wahrscheinlichkeiten von P
in eindeutiger Weise durch w festgelegt. Mit anderen Worten: Kennt man
w, so kennt man auch P für X. Nach dem
Produktionsgesetz für unabhängigen Zufallsvariablen gilt für
P:
P[x1,x2,...,xT] = P
(P[X=zt|w])
Diese sogenannte Maximum-Likelihood-Funktion liefert in Abhängigkeit von
der Schätzung wh der Parameter w eine bestimmte
Wahrscheinlichkeit für die erhobenen Variablenausprägungen
zurück. Ziel ist es, diejenigen Parameter wh zu bestimmen, bei dem
die beobachteten x1,x2,...,xT bei dem
gegebenem P am wahrscheinlichsten sind. Um dieses funktional gegebene
Maximum der Likelihood-Funktion zu finden, wird sie üblicherweise erst
einmal durch Logarithmierung in Summenform transformiert. Das ist ohne
Änderung der Positionen der Extrema möglich. Für den Logarithmus
gilt:
ln(a×b) = ln(a)+ln(b).
Man erhält so die zu maximierende Log-Likelihood-Funktion
L(w) = S(ln(P[X=xt|w])
Um zu verstehen, wie eine neurometrische Schätzung über die
Maximum-Likelihood-Methode vorgenommen wird, sei nun das folgende einfache
neuronale Netzwerk betrachtet:
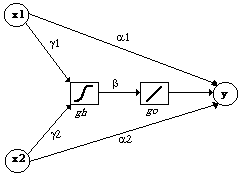
Wie zu erkennen, allokiert das Modell insgesamt fünf Parameter:
w=(g1,g2,b,a1,a2).
Als Eingabevektoren dienen die unabhängigen Variablen
x1 und x2. Sie bestehen jeweils aus
T Beobachtungen und bilden zusammen die Eingabematrix
X=(x1,x2). Die (sigmoide) Aktivierungsfunktion des
versteckten Neurons ist mit gh, die (lineare) Ausgabefunktion mit
go bezeichnet. Vom Modell geliefert wird die univariate Variable
y. Typische Kandidaten für die Transfer- und Ausgabefunktion plus
erster und zweiter Ableitung sind z.B.:
Zur Bildung der Maximum Likelihood-Funktion (= negierte Kostenfunktion) wird
folgende Formel herangezogen:
L(w,W,X) = -ln|W|
-[F(X)-f(w,X)]T×
W-1×
[F(X)-f(w,X)],
wobei F(X) die zu approximierende Funktion,
f(w,X) die Netzwerkfunktion und
W die Kovarianzmatrix der Parameter bezeichnet.
Sie basiert auf der Dichtefunktion der multivariaten Normalverteilung:
f(x) = 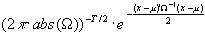
Für das oben dargestellte neuronale Netzwerk ergibt sich dadurch
folgende Formelsammlung:
-
Residuen: u = F(X)-f(w,X); Soll-Ist-Abweichungen
-
Netzwerkfunktion:
f(w,X) =
go(ro)+
a1×x1
+a2×
x2;
Ist-Output des Modells
-
Received Output:ro = b×sh;
Signale, die an das Ausgabeneuron gehen
-
Signal Hidden: sh = gh(rh); Signale, die vom versteckten Neuron kommen
-
Received Hidden: rh = g1×
x1+g2×
x2;
Signale, die ans versteckte Neurone gehen
Unter der Annahme, dass die Residuen multivariat normalverteilt sind mit
Erwartungswert Null, entspricht die Kovarianzmatrix W
dem konstantem Term
s2×I, wobei
s2 die
Varianz der Schätzung und I die Einheitsmatrix wiedergibt. Damit
ist die Kovarianzmatrix unabhängig von den Gewichten und kann in der zu
maximierenden negierten Kostenfunktion vernachlässigt werden. Man
erhält:
KF(w,X) = -u2 »
-½×
u2 »
L(w,W,X).
Aus der mathematischen Kurvendiskussion ist bekannt, dass im univariaten
Fall die erste Ableitung einer Funktion im Maximum Null sein muss. Im
multivariaten Fall gilt dies in analoger Weise für den Gradienten. Dieser
setzt sich aus den ersten partiellen Ableitungen nach w
an der Stelle (w,X) zusammen. Die
benötigten partiellen Ableitungen erster Ordnung lassen sich
folgendermassen formulieren:
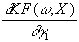 = u×
go’(ro)×
b×
gh’(rh)×
x1
= u×
go’(ro)×
b×
gh’(rh)×
x1
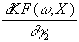 = u×
go’(ro)×
b×
gh’(rh)×
x2
= u×
go’(ro)×
b×
gh’(rh)×
x2
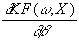 = u×
go’(ro)×sh
= u×
go’(ro)×sh
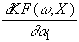 = u×
x1
= u×
x1
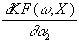 = u×
x2
= u×
x2
Für den Gradienten gilt dann:
g = 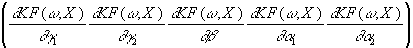
Aus der mathematischen Kurvendiskussion ist ebenfalls bekannt, dass im
univariaten Fall geprüft werden muss, ob die zweite Ableitung der
betrachteten Funktion kleiner als Null ist, da sie sonst an der Stelle
(w,X) auch ein Minima oder einen Sattelpunkt
besitzen kann. Analog dazu wird im multivariaten Fall geprüft, ob die
Hessematrix negativ definit ist. Sie wird gebildet aus den zweiten partiellen
Ableitungen nach w
an der Stelle (w,X). Die benötigten
partiellen Ableitungen zweiter Ordnung lassen sich folgendermassen
formulieren:
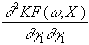 =
b×
x1×
x1×
[go’2(ro)×
b
×
gh’2(rh)-u×
go’’(ro)×
gh’2(rh)×
b
+u×
go’(ro)×
gh’’(rh)]
=
b×
x1×
x1×
[go’2(ro)×
b
×
gh’2(rh)-u×
go’’(ro)×
gh’2(rh)×
b
+u×
go’(ro)×
gh’’(rh)]
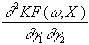 =
b×
x1×
x2×
[go’2(ro)×
b
×
gh’2(rh)-u×
go’’(ro)×
gh’2(rh)×
b
+u×
go’(ro)×
gh’’(rh)]
=
b×
x1×
x2×
[go’2(ro)×
b
×
gh’2(rh)-u×
go’’(ro)×
gh’2(rh)×
b
+u×
go’(ro)×
gh’’(rh)]
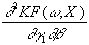 =
gh’(rh)×
x1×
[go’2(ro)×
sh×
b
+u×
go’’(ro)×
sh×
b
+u×
go’(ro)]
=
gh’(rh)×
x1×
[go’2(ro)×
sh×
b
+u×
go’’(ro)×
sh×
b
+u×
go’(ro)]
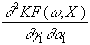 =
-go’(ro)×
b
×
gh’(rh)×
x1×
x1
=
-go’(ro)×
b
×
gh’(rh)×
x1×
x1
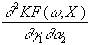 =
-go’(ro)×
b
×
gh’(rh)×
x1×
x2
=
-go’(ro)×
b
×
gh’(rh)×
x1×
x2
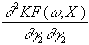 =
b×
x2×
x2×
[go’2(ro)×
b
×
gh’2(rh)-u×
go’’(ro)×
gh’2(rh)×
b
+u×
go’(ro)×
gh’’(rh)]
=
b×
x2×
x2×
[go’2(ro)×
b
×
gh’2(rh)-u×
go’’(ro)×
gh’2(rh)×
b
+u×
go’(ro)×
gh’’(rh)]
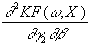 =
gh’(rh)×
x2×
[go’2(ro)×
sh×
b
+u×
go’’(ro)×
sh×
b
+u×
go’(ro)]
=
gh’(rh)×
x2×
[go’2(ro)×
sh×
b
+u×
go’’(ro)×
sh×
b
+u×
go’(ro)]
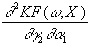 =
-go’(ro)×
b
×
gh’(rh)×
x2×
x1
=
-go’(ro)×
b
×
gh’(rh)×
x2×
x1
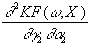 =
-go’(ro)×
b
×
gh’(rh)×
x2×
x2
=
-go’(ro)×
b
×
gh’(rh)×
x2×
x2
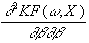 =
sh×
[go’2(ro)×
sh+u×
go’’(ro)×
sh]
=
sh×
[go’2(ro)×
sh+u×
go’’(ro)×
sh]
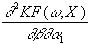 =
-go’(ro)×
sh×
x1
=
-go’(ro)×
sh×
x1
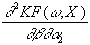 =
-go’(ro)×
sh×
x2
=
-go’(ro)×
sh×
x2
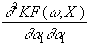 =
-x1×
x1
=
-x1×
x1
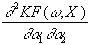 =
-x1×
x2
=
-x1×
x2
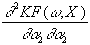 =
-x2×
x2
=
-x2×
x2
Da die Hessematrix symmetrisch ist, genügen zu ihrer Berechnung die
fünfzehn obigen partielle Ableitungen zweiter Ordnung, obwohl sie im
betrachteten Fall insgesamt die Dimension 5 x 5 besitzt. Für die
Hessematrix gilt also:
H = 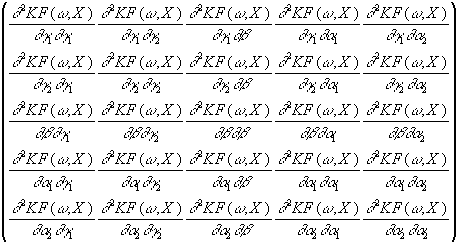
Anhand des Beispiels wird die Komplexität deutlich, die bereits einfache
neuronale Netze auszeichnet. Die Berechnung des Gradienten und der Hessematrix
erschwert sich mit wachsender Zahl der Neuronen in der ersten versteckten
Schicht noch erheblich. Es kommen dann zusätzliche Ableitungsfälle
hinzu, da die einzelnen Kantengewichte jeweils unterschiedlichen versteckten
Neuronen bzw. unterschiedlichen Ausgabeneuronen zuzuordnen sind. Es gilt in
diesem Fall allgemein:
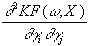 =
gh(rhj)×
b
i×
b
j×
xi×
xj×
gh’(rhi)×
[go’2(ro)+u×
go’’(ro)]
mit
iÎI,
jÎJ und
IÈJ=0
=
gh(rhj)×
b
i×
b
j×
xi×
xj×
gh’(rhi)×
[go’2(ro)+u×
go’’(ro)]
mit
iÎI,
jÎJ und
IÈJ=0
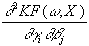 =
shj×
b
i×
gh’(rhi)×
xi×
[go’2(ro)+u×
go’’(ro)]
mit
iÎI,
jÎJ und
IÈJ=0
=
shj×
b
i×
gh’(rhi)×
xi×
[go’2(ro)+u×
go’’(ro)]
mit
iÎI,
jÎJ und
IÈJ=0
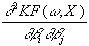 =
=
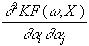 =
0 mit
iÎI,
jÎJ
und
IÈJ=0
=
0 mit
iÎI,
jÎJ
und
IÈJ=0
Alle bisher gezeigten Formeln behalten ihre Geltung auch bei Verwendung
alternativer Aktivierungs- und Ausgabefunktionen. Eine zu beachtende
Restriktion dabei ist jedoch, dass die Aktivierungsfunktion in jedem Fall
zweimal stetig different sein muss (ein konstante erste oder zweite
Ableitung ist dagegen unproblematisch).
Mithilfe von Neurometricus lässt sich der analytische Gradient nicht
nur bei keiner oder einer versteckten Schicht berechnen, sondern auch bei
beliebig vielen versteckten Schichten. Auf eine Darstellung der dazu
nötigen mathematischen Formalismen sei hier verzichtet. Zu ihrer
Realisierung sind verschachtelte Iterationsschleifen sowie rekursive
Algorithmen vonnöten, die für den Leser über den Sourcecode von
Neurometricus leichter nachzuvollziehen sind. Eine analytische Berechnung der
Hessematrix bei Vorhandensein mehrerer versteckter Schichten ist mit
Neurometricus derzeit nicht möglich. Die "maxlik"-Prozedur
bekommt in diesem Fall einen Zeiger überwiesen, der auf eine Funktion
verweist, über die die Hessematrix auf numerischem Weg bestimmt wird.
ANHANG D: Gradientenabstriegsverfahren
Es sei
X die unabhängigen Variablen,
y die unabhängige Variable,
w die Parameter der Log-Likelihood-Funktion,
k die Anzahl der Parameter,
t die Anzahl der Beobachtungen je Variable,
q(w,y,X) die Log-Likelihood-Funktion,
q’(w,y,X) der Gradienten der Log-Likelihood-Funktion abgeleitet nach w,
q’’(w,y,X) die Hessematrix der Log-Likelihood-Funktion abgeleitet nach w,
n der Index für den n-ten Iterationsschritt,
Q die Richtungsmatrix,
d(w) die Abstiegsrichtung,
h die skalare Schrittweite in der Abstiegsrichtung d(w).
Dann erzeugen die Gradientenabstiegsverfahren theoretisch eine
Folge q(w0), q(w1), ..., q(wN)
mit der Eigenschaft, sodass gilt:
q(wn+1) < q(wn).
Als allgemeines Bildungsgesetz für das Parameter-Update
wn+1 wird verwendet:
wn+1 = wn - h
n×
d(wn) = wn - h
n×
Qn×
q’(wn,y,X).
Der Richtungsvektor d basiert in Neurometricus auf folgender Gleichung
C×d = q’,
wobei q’ die Dimension k x 1 besitzt und C eine obere
Dreiecksmatrix der Grösse k x k darstellt. C wird durch
eine Cholesky-Faktorisierung aus der symmetrischen k x k-Matrix
q’’ gewonnen. Es gilt dann:
q’’ = CTC.
Zur Bestimmung des Richtungsvektors d lassen sich demnach folgende
Formeln einsetzen:
d = q’’-1×q’ oder
d = C-1×q’.
Es hat sich herausgestellt, dass die Invertierung der
Choleky-Dekomposition numerisch stabiler und schneller ist als die Invertierung
der vollen Hessematrix. C-1 oder q’’-1
stellt die (oben mit Q gekennzeichnete) Richtungsmatrix dar. Warum dies
so ist, wird gleich am Beispiel des Newton-Verfahrens erkenntlich. Doch zuvor
einige allgemeine Hinweise: Die Gradientenabstiegsverfahren lassen sich durch
die Art der Berechnung von Q in eindeutiger Weise identifizieren.
Basiert Q in jedem Iterationsschritt auf der Hessematrix bzw. einer
Approximation der Hessematrix, so spricht man von Optimierungsverfahren zweiter
Ordnung. Wird ein Substitut von Q verwendet, z.B. das
Gradientenkreuzprodukt oder die Einheitsmatrix, liegt ein Optimierungsverfahren
erster Ordnung vor.
Es sei die Approximation der Taylorreihe zweiter Ordnung der Zielfunktion
q mit q^ bezeichnet. Dann gilt im Rahmen des Newton-Verfahrens:
q(w,y,X) »
q^(w,y,X) = q(wn) + q’(w-wn,y,X)+
0.5×
(w-wn)T×
q’’(w-wn,y,X)
Extrema von q^ lassen sich durch die Bestimmung der Nullstellen von
q^’ finden:
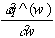 =
q’(wn,y,X) + q’’(w-wn,y,X) = 0.
=
q’(wn,y,X) + q’’(w-wn,y,X) = 0.
Daraus folgt:
w = wn - q’’-1(wn,y,X)×
q’(wn,y,X).
Aus der weiter oben gezeigten Formel für das Update von w in jedem
Iterationsschritt lässt sich dann zeigen:
Qn = q’’-1(wn,y,X).
Zur Verdeutlichung der beschriebenen Zusammenhänge sei folgendes lineare
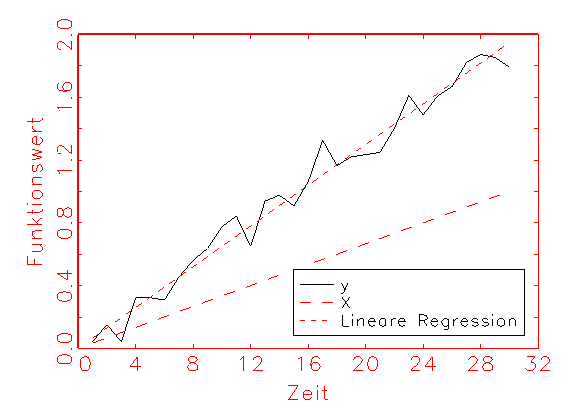
Regressionsproblem gegeben:
X = (0.033,0.066,0.1,...,1)
y = 2×X+normalverteiltes Rauschen mit Mittelwert=0 und Varianz=0.2
wn = 0.1 die Startinitialisierung des zu schätzenden Parameters
Grafisch ergeben y und X folgende Zeitreihen:
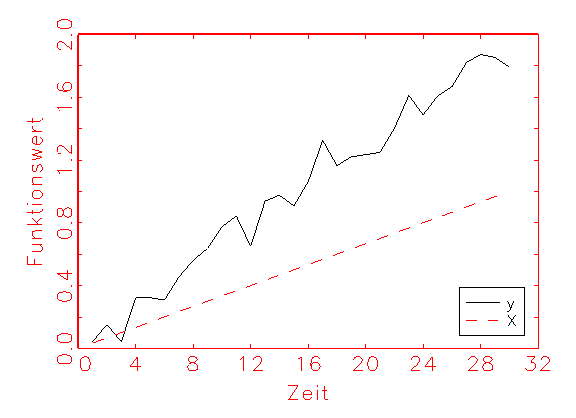
Es ist nun auf numerischem Wege y linear auf X zu regressieren.
Zielfunktion ist der negierte MSE des linearen Regressionsmodell, also:
y = X×
wn + e
negierter MSE = q(wn,y,X) = -S
(y-X×
wn)2.
Das Newton-Verfahrens lässt sich - vereinfacht - durch folgende
Prozedur realisieren:
DO WHILE Zielfunktionsverbesserung erreicht;
qvalue = q(wn,y,X); //Zielfunktionswert
gradient = gq(wn,y,X); // Gradienten (numerisch/analytisch)
hesse = hq(wn,y,X); // Hesse (numerisch/analytisch)
d = hesse-1*× gradient; // Richtungsvektor
wn = wn+Schrittlänge*×d; // Parameter-Update
ENDO;
Nach nur zwei Iterationsschritten wird das Maximum der negierten Kostenfunktion
gefunden. Der Parameter wn nimmt dabei die Werte 0.1, 1.9534
und 1.947728 an. Als Regressionsgerade yh = X×
w3 ergibt sich:
Die anderen Gradientenabstiegsverfahren zweiter Ordnung berechnen die
Hessematrix als Basis für die Richtungsmatrix Q nur in der ersten
Iteration. Danach wird die Richtungsmatrix Q in jedem Schritt durch eine
Matrix Kn korrigiert:
Qn+1 = Qn + Kn
Dabei wird die Matrix Kn so gewählt, dass
Qn+1 positiv definit bleibt. Noch einfacher machen es sich
die sogenannten Scoring-Verfahren, die lediglich mit dem Erwartungswert der
Hessematrix arbeiten, der sich aus dem Gradientenkreuzprodukt zusammensetzt:
Qn = -E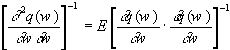 .
.
Gradientenabstiegsverfahren der ersten Ordnung ersetzen die Hessematrix durch
eine Einheitsmatrix der gleichen Dimension. Sie konvergieren dadurch in der
Nähe des Optimums deutlich langsamer. Durch einen speziellen Term
kn, der von Polak und Ribiere vorgeschlagen wurde, lassen sich
jedoch auch diese Verfahren effizienter gestalten. Der Richtungsvektor d
berechnet sich dann in jedem Iterationsschritt durch:
dn+1 = q’’(wn,y,X) + kn×
dn,
wobei kn folgermassen entwickelt wird:
kn = 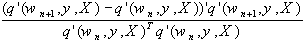 .
.
ANHANG E: Ein Känguruh im Himalaya
(inspiriert von W. Sarle 1994a)
Vorgeschichte
Ein Känguruh (Maximierungsprozess) erhält den Auftrag, den Mount
Everst (globales Maximum) zu finden. Notfalls würde auch der K2 akzeptiert
werden, nicht aber z.B. der Winterberg im Sauerland. Das Känguruh wird
irgendwo mit dem Fallschirm aus einem Flugzeug abgeworfen (Initialisierung der
Startgewichte mit einem Zufallswert). Es landet dabei umso näher am
Zielgebiet, je besser der Pilot die Landschaft kennt (Einschränkung des
Zufallsbereichs der Gewichteinitialisierung).
Nach dem Abwurf ...
Das Känguruh kauert auf dem Boden, um es herum ist dichter Nebel. Wie soll
es in dieser undurchsichtigen Suppe bloss den Mount Everest finden
können? Nach langen Grübeln hat es sich schliesslich einige
Strategien zurechtgelegt.
Lokale Sprungstrategien
Die folgenden Strategien verhelfen dem Känguruh stets auf einen Berggipfel
hinauf. Es ist aber keineswegs sichergestellt, dass es sich dabei auch um
den Gipfel des Mount Everest handeln wird.
-
Online-Backpropagation: Das Känguruh hat mit erschwerten
Bedingungen zu kämpfen, denn durch Erdbeben schrumpfen und wachsen die
Berge in seiner Nähe ständig (Online-Gewichtung des Netzwerks).
Dadurch kann es nur schwerlich eine Sprungrichtung finden, weshalb es sich mit
vielen kleinen, wenig gezielten Hüpfern (Iterationen) behilft.
-
Steilster Aufstieg: Jetzt bleibt die Umgebung stabil. Das Känguruh
grübelt daher auch nicht lange, sondern sucht sich einfach die steilste
Stelle in seiner lokalen Umgebung (Gradientenmaximum) und springt in diese
Richtung. Dort angekommen sucht es nach der nächsten steilen Stelle und
springt weiter, bis es schliesslich auf dem höchsten Punkt angekommen
ist (Gradient gleich Null). Das geht zwar schnell, kann aber auch auf dem
Winterberg im Sauerland enden.
-
Konjugierter Gradientenabstieg: Das Känguruh verhält sich
ähnlich wie in (2), jedoch merkt es sich diesmal die jeweilige
Sprungrichtung. Findet es einen steilsten Aufstieg in einer anderen Richtung,
folgt es diesem nur bedingt. Im Mittel springt es lieber in der gleichen
Richtung den Berg herauf. Es glaubt: "In der Richtung, in der es insgesamt
am meisten nach oben führt, da wird am Ende auch der Mount Everest zu
finden sein."
-
Scoring-Verfahren: Statt wie in (5) lange nach einer quadratischen Form
zu suchen, benutzt das Känguruh die steilste Stelle in seiner Umgebung, um
die vielversprechenste Sprungrichtung zu bestimmen (Gradientenkreuzprodukt).
Danach macht es jedoch im Prinzip das Gleiche wie in (5).
-
Quasi-Newton: Das Känguruh spring in die Richtung, in der es eine
schöne quadratische Form erkennen kann (quadratische
Taylorreihenapproxmiation). Kann es diese nicht mit einem einzigen Sprung
erreichen, korrrigiert es seine Richtung ein wenig und probiert es erneut
(Approximation der Hesse). Es denkt sich: "Lieber hüpfe ich oft,
schnell und ungenau, als wenig, langsam und genau."
-
Newton-Raphson: Das Känguruh springt wie in (5) in die Richtung, in
der es eine quadratische Form ausmachen kann. Muss es mehrmals springen,
so berechnet es jedes Mal auf ’s neue die beste Sprungrichtung (Berechnung der
Hesse). Oben angekommen, kann es dennoch nur hoffen, dass es sich um den
Mount Everest handelt.
Globale Sprungstrategien
Die folgenden Strategien führen das Känguruh früher oder
später auf den Mount Everest hinauf. Im Mittel jedoch eher später als
früher ...
-
Simuliertes Ausglühen: Das Känguruh besäuft sich
erst einmal und hüpft dann ziemlich planlos (stochastisch) in der
Landschaft herum. Je länger es dies tut, desto nüchterner wird es
jedoch, und um so wahrscheinlicher wird es, dass es auf dem höchsten
Gipel landet.
-
Genetische Algorithmen: Das Känguruh ruft seine Kumpels zu Hilfe,
die auch prompt von überall her kommen. Leider haben sie keine Ahnung,
dass sie den Mount Everest suchen sollen. Da jedoch die in den tieferen
Ebenen hüpfenden Känguruhs von Jägern eingefangen werden,
mutieren die Känguruhs dahin gehend, dass sie sich lieber in
höheren Gefilden herumtreiben. Irgendwann wird eines davon
schliesslich auf dem Mount Everest landen.
-
Sintflut-Algorithmus: Das Känguruh hüpft auf den erst besten
Hügel und wartet dort auf die nächste Sintflut. Wenn das Wasser die
Hügelspitze erreicht hat, guckt es um sich, springt ins Wasser und
schwimmt zum nächsten Gipfel, um dort auf eine weitere Sintflut zu warten.
Irgendwann einmal wird es so auf dem Mount Everest landen.
ANHANG F: Berechnung der Kovarianz der Parameter
Es sei
t die Anzahl der Beobachtungen,
k die Anzahl der Modellparameter,
i die Anzahl unabhängiger Variablen,
X eine t x i-Matrix mit unabhängigen Variablen,
y ein t x 1-Vektor mit einer abhängigeVariable.
Betrachtet wird das lineare Regressionsmodell
y = X×w+e.
In diesem Fall gilt i = k, d.h. jeder Modellparameter ist genau einer
X-Variablen zugeordnet. Aus der Grösse des Parameters nach der
Schätzung kann auf die Bedeutung der X-Variable für die
Regression geschlossen werden. Die Kovarianzmatrix der Parameter berechnet sich
durch:
cov = 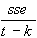 (X’X)-1.
(X’X)-1.
Auf Basis der Kovarianzmatrix der Parameter werden diverse weiterführende
Statistiken berechnet, z.B. die Korrelationsmatrix, die Standardabweichung, die
t-Werte der Parameter usw. Bei der Diagnose der Parameter einer
Schätzung nimmt also die Kovarianzmatrix und insbesondere der enthaltene
(X’X)-1-Term eine wesentliche Rolle ein.
Betrachtet wird nun ein nichtlineares Regressionsmodell (welches durch ein
neuronales Netzwerk abgebildet wird). In diesem Fall gilt:
y = F(w,X)+e,
wobei F die wahre Funktion darstellt, die durch die Netzwerkfunktion
f approximiert werden soll. Die Approximation f wird determiniert
durch die Modellparameter wh, die einer Schätzung der optimalen
Parameter w der wahren Funktion F entsprechen. Sei
wh=(g
1,...,g
G,b
1,...,b
B,a
1,...,a
A),
gemäss der in der Arbeit angegeben Konventionen für die Gewichte
von Neurometricus-Netzwerken. Dann ist die Netzwerkfunktion in Matrixnotation
yh = f(wh,X) = go(gh(X×
g
)×
b
)+X×
a,
wobei go die Ausgabefunktion und gh die Aktivierungsfunktion
bezeichnen. Hier gilt, dass die Anzahl der Modellparameter k
grösser als die Anzahl der unabhängigen Variablen i
ausfallen kann. Da die (X’X)-1-Matrix nur die Dimension
i x i besitzt, kann sie dann zur Berechnung der Kovarianz der k
Parameter nicht immer herangezogen werden. Im nichtlinearen Fall muss die
(X’X)-1-Matrix daher durch eine Schätzung substituiert
werden. Eine solche Schätzung ist - asymptotisch - mit der inversen
Hessematrix der Kostenfunktion h-1 bzw. dem inversen
Gradientenkreuzprodukt der Kostenfunktion gc-1 an der Stelle
(wh,y,X) gegeben. Sie besitzt die geforderte Dimension k x k und
entspricht exakt der (X’X)-1-Matrix, wenn wh nur aus
Alpha-Gewichten besteht. Für die im linearen und nichtlinearen Fall
asymptotisch gültige Kovarianzmatrix der Parameter gilt also:
cov = 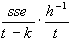 und
und
cov = 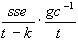
Durch eine Kombination der Hessematrix und dem Gradientenkreuzprodukt kann eine
heteroskedastie-konsistente Kovarianzmatrix der Parameter berechnet werden. Sie
besitzt den Vorteil, auch dann unverzerrt und asymptotisch effizient zu sein,
wenn die Streuung der Residuen des zugrunde liegenden Modells nicht konstant
ist. Dadurch behalten die oben erwähnten weiterführenden Statistiken
im Falle von Heteroskedastizität ihre Gültigkeit bei. Die Formel der
heteroskedastie-konsistenten Kovarianzmatrix der Parameter ist
cov = 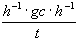 .
.
ANHANG G: Formelsammlung für Neurometricus
Sei i die Anzahl der Eingabevariablen, o die Anzahl der
Ausgabevariablen, t die Anzahl der Beobachtungen und k der
Freiheitsgrad des zugrunde liegenden Modells. Dann gilt:
- Eingabevariablen: x = t x i-Matrix
- Ausgabevariablen: y = t x o-Matrix
- Aktuelle Modellparameter:
- Normal: wh = k x 1-Vektor mit geschätzen Log-Likelihood-Parameter
- Nach v Resampling-Schätzungen:
-
Matrixform: wh = v x k-Matrix mit v geschätzten
Log-Likelihood-Parametern. Liefert für die meisten der folgenden Statisiken
statt Skalaren v x 1-Vektoren zurück.
- Vektorform: wh = k x 1-Vektor mit Mittelwerten der Resampling-Matrix
- Approximationsfunktion: yh = t x o-Matrix mit Netzfunktion(wh,x)-Werten
- Residuen: u = y-yh
- Negierter Gradient der Kostenfunktion (1.Ableitung nach Zeit):
- Analytisch: g = t x o-Matrix
- Numerisch: g = n x o-Matrix
- Negierter Gradient der Kostenfunktion (1.Ableitung nach Parametern):
- Analytisch: gw = k x o-Matrix
- Numerisch: gw = k x o-Matrix
-
Gradientenkreuzprodukt der Kostenfunktion:
gc =
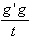
- Negierte Hessematrix der Kostenfunktion geteilt durch t:
- Analytisch: h = k x k-Matrix
- Numerisch: h = k x k-Matrix
-
Sum of Errors:
se =
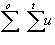
-
Absolute Sum of Errors:
ase =
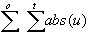
- Sum of Squared Errors:
- Ein Output: sse = u’u
- Mehrere Outputs: sse = det(u’u)
-
Sum of Errors u/y:
seuy =
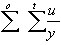
-
Absolute Sum of Errors u/y:
seuy =
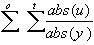
-
Varianz der Schätzung:
var =
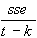
- Kovarianz:
- Normal: c =
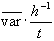
- Subsitut: c =
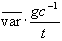
- Heteroskedastie-konsistent: c =
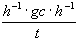
-
Sum of Total Errors:
sst =
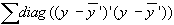
-
Durbin Watson-Statistik:
dw =
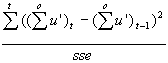
-
Mean Squared Error:
mse =
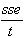
-
"Echte" Log-Maximum-Likelihood:
lml =
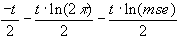
-
Standardabweichung der Parameter:
stdpara =
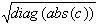
-
t-Statistik der Parameter:
tstat =
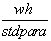
-
Transformierter Kostenfunktionswert:
qv =
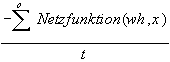
-
Akaike-Informationskriterium:
aic =
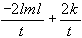
-
Schwarz-Informationskriterium:
sic =
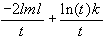
-
Netzwerk-Informationskriterium:
nic =
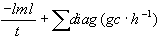
-
Godness of Fit-Selektionskriterium:
r2 =
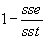
-
Godness of Fit-Selektionskriterium (justiert):
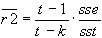
-
F-Statistik der Schätzung:
fstat =
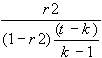
-
Prediction Criterion:
pc =
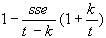
-
Final Prediction Error:
fpe =
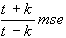
-
Root Mean Squared Error:
rmse =
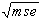
-
Mean Error:
me =
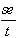
-
Mean Percent Error:
mpe =
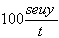
-
Mean Absolute Error:
mae =
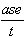
-
Mean Absolute Percent Error:
mape =
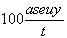
-
Standardnormalverteilung beim a/2-Sicherheitsniveau:
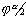 = Tabellenwert
= Tabellenwert
-
Konfidenzintervall:
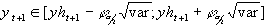
Formeln der Normierung
Sei xt eine n x k-Matrix, xmin
der k x 1 Vektor der Minima von xt und
xmax der k x 1 Vektor der Maxima von xt.
Dann gilt für die [a,b]-Intervall-Normierung:
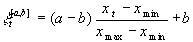 .
.
Sei xt eine n x k-Matrix, m
x der k x 1 Vektor der Mittelwerte von xt und s
x der k x 1 Vektor der Varianzen von xt.
Dann gilt für die Mittelwert-Varianz-Normierung:
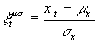 .
.
ANHANG H: Wirkungsweise des konstanten Eingabevektors
Betrachtet werden die univariaten Zeitreihen (Variablen)
x = {0.02, 0.04, 0.06, ..., 0.98, 1},
c = {1, 1, 1, ..., 1, 1} und
y = 0.5+x2.
Eine lineare Einfachregression ohne Konstante regressiert y auf x folgendermassen:
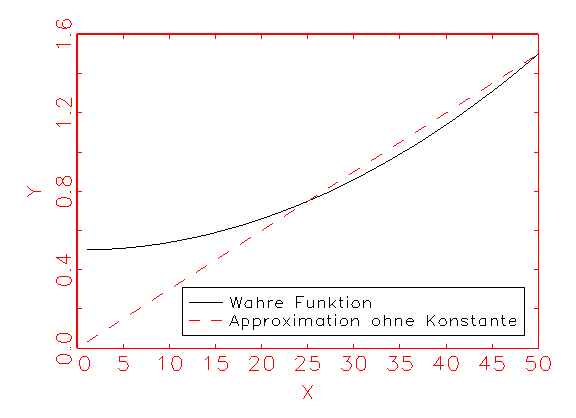
Ohne einen konstanten Eingabevektoren wird jede Regression "gezwungen",
durch den Ursprung zu verlaufen. Im Beispiel führt das zu einer erheblichen
Verzerrung der Regression, da y oberhalb von Null die Ordinate kreuzt. Von
grösserer Güte fällt daher die Regression aus, wenn y auf x
und c regressiert wird, wie folgende Abbildung demonstriert:
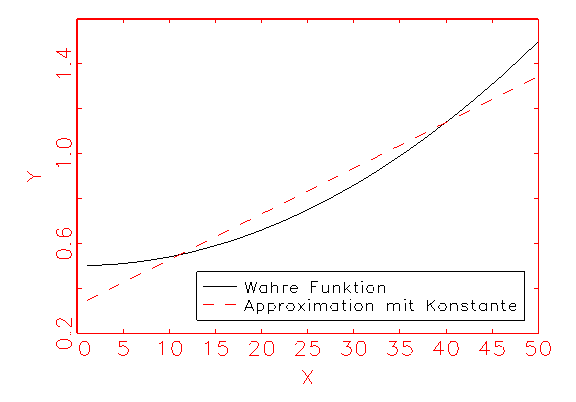
Untenstehende Tabelle gibt das grafisch gezeigte Ergebnis in metrischer Form wieder.
Als Gütemass für die Schätzung des Modells wurde dabei das in
der Statistik übliche R2-Kriterium herangezogen.
| |
Güte |
Varianz |
| Regression ohne Konstante |
0.66507531 |
0.0315136 |
| Regression mit Konstante |
0.93987136 |
0.0057754667 |