Diplomarbeit - Konstruktion von NN für Regressionsanalysen - Kapitel 2.2
von Daniel Schwamm (09.11.2000)
Ziel jeder ökonometrischen Untersuchung ist die Erklärung oder
Prognose von ökonomischen Variablen. Zu diesem Zweck unterstellt man
zwischen den Variablen einen unbekannten Zusammenhang, den es aufzudecken gilt.
In den wenigsten Fällen gelingt es dabei, die wahre Funktion zu finden,
die die funktional Beziehung exakt beschreibt. Im Rahmen der
Approximationstheorie, die diese Problematik mathematisch behandelt, werden
jedoch statistische Methoden angeboten, über die der gesuchte Zusammenhang
durch eine Näherungsfunktion beschreibbar gemacht werden kann.
Im folgenden wird eine Übersicht über die statistische Theorie
gegeben. Die dabei erläuterten Begriffe sind für das weitere
Verständnis der vorliegenden Arbeit nötig. Zur leichteren
Orientierung für den Leser erfolgt die Beschreibung gemäss der
hierarchischen Klassifizierung der statistischen Theorie, wie sie in Abbildung
2.4 vorgegeben ist. Auf die gebräuchlichsten Werkzeuge zur Erklärung
unbekannter Zusammenhänge zwischen Variablen, die Regressionsmodelle, wird
in Abschnitt 2.3 eingegangen. Für eine tiefer gehende Erklärung der
angesprochenen Punkte sei auf Hansen (1985), Rinne (1988) und Hochstädter
(1989) verwiesen.
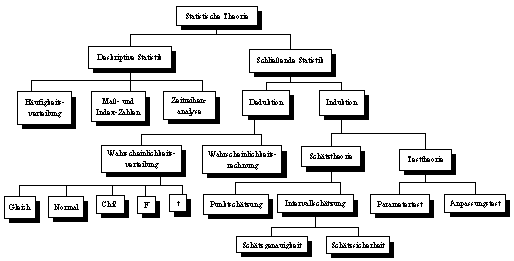
Abbildung 2.4: Hierarchische Klassifizierung der statistischen Theorie.
Quelle: Angelehnt an Hochstädter (1989), S. 409 ff.
Es ist die Aufgabe der deskriptiven Statistik, Informationen über die
Struktur von beobachtbaren Erscheinungen, zum Beispiel des Wirtschaftslebens und
Soziallebens, zu sammeln, aufzubereiten und zu charakterisieren. Die
betrachtete Grundgesamtheit erfährt durch die zu untersuchenden Merkmale
eine Abgrenzung in sachlicher, räumlicher und zeitlicher Hinsicht von
anderen Grundgesamtheiten. Merkmale einer Grundgesamtheit, deren
Ausprägung (in der Zeit qualitativ oder quantitativ) variieren, werden
auch Variablen genannt. Die Zuordnung von Häufigkeiten zu einer einzelnen
Variable beschreibt die eindimensionale Verteilung einer Grundgesamtheit. Sie
wird grafisch in Form von Histogrammen dargestellt. Besitzt eine Verteilung
zwei beziehungsweise mehr als zwei Maxima, so nennt man sie bimodal
beziehungsweise multimodal, werden mehrere Variablen simultan
berücksichtigt, so ist sie mehrdimensional.
Die Zentralwerte (arithmetisches Mittel, Median und Modus) geben eine
quantitative Beschreibung der durchschnittlichen (typischen) Leistung der
Grundgesamtheit bezüglich eines Merkmals wieder. Masszahlen der
Streuung (Rang und Standardabweichung) und Masszahlen der Schiefe
beziehungsweise Wölbung einer Verteilung ergänzen die
Charakterisierung der betrachteten Grundgesamtheit. Die Masszahlen werden
auch als Parameter der Grundgesamtheit bezeichnet.
Mithilfe von dimensionslosen Messzahlen kann man zwei oder mehrere
gleichartige Grundgesamtheiten untereinander vergleichen. Indexzahlen zum
Beispiel sind Messzahlen des zeitlichen Vergleichs komplexer
Grössen, wobei der Einfluss der den Vergleich störenden
Komponenten durch Konstanthaltung über die Zeit rechnerisch ausgeschaltet
wird. Die Messzahlen werden vor allem im Zusammenhang mit Zeitreihen
erhoben. Unter einer Zeitreihe versteht man eine zeitlich geordnete Folge von
Beobachtungen einer Variablen (univariate Zeitreihe) oder mehrerer Variablen
(multivariate Zeitreihe).
Man betrachte eine Grundgesamtheit, deren stochastische Eigenschaften
bezüglich einer oder mehrerer Variablen als bekannt vorausgesetzt werden.
Zieht man nach dem Zufallsprinzip aus dieser Grundgesamtheit eine Stichprobe,
so lassen sich a priori Aussagen über gewisse Stichprobenergebnisse
machen. Diese Vorgehensweise bezeichnet man als deduktiven Schluss in der
Statistik, wobei die Wahrscheinlichkeitsrechnung eine mathematische Beziehung
zwischen der Stichprobe und der Grundgesamtheit mit einer endlichen Anzahl von
Variablen herstellt. Für die praktische Anwendung ist jedoch die
umgekehrte Vorgehensweise interessanter, die man als induktiven Schluss in
der Statistik bezeichnet. Die Stichprobe wird dann benutzt, um
Rückschlüsse über die unbekannte Verteilung der betrachteten
Variablen in der Grundgesamtheit zu ziehen. Zentrale Aufgaben der induktiven
Statistik sind das Schätzen von Wahrscheinlichkeiten und das Testen von
Hypothesen.
Als Zufallsexperiment wird ein Versuch bezeichnet, dessen Ergebnis a priori nicht mit
Sicherheit voraussagbar ist. So ist zum Beispiel die Ziehung einer Stichprobe aus einer
Grundgesamtheit ein Zufallsexperiment, sofern jeder Wert der betrachteten Variablen
die gleiche Chance hat, in die Stichprobe einzugehen. Das mögliche Ergebnis eines
solchen Zufallsexperiments bezeichnet man als Ereignis. Zwei Ereignisse haben genau
dann die gleiche Chance gezogen zu werden, wenn sie voneinander stochastisch
unabhängig sind, d.h., wenn die Wahrscheinlichkeit für das Eintreten des
einen Ereignisses nicht davon abhängt, ob das andere Ereignis eingetreten ist
oder nicht. Eine eindimensionale Zufallsvariable ist eine Funktion,
die jedem Ereignis des Ereignisraums eine reelle Zahl zuordnet, sodass
für jede Realisation der Zufallsvariablen die Wahrscheinlichkeit definiert ist.
In gleicher Weise ist eine mehrdimensionale Zufallsvariable eine Funktion, die jedem
Ereignis des Ereignisraums mehrere reelle Zahlen zuordnet.
Wie für deterministische Merkmale, so lassen sich auch für
Zufallsvariablen Masszahlen aufstellen. Das gewogene arithmetische Mittel
der Beobachtungen einer stetigen Zufallsvariable wird zum Beispiel als
Erwartungswert bezeichnet. Es hat sich in empirischen Untersuchungen gezeigt,
dass die quantitativen Daten natürlicher/zufälliger Ereignisse
annähernd durch eine Normalverteilung beschrieben werden können. Nach
dem zentralen Grenzwertsatz lassen sich über die Masszahlen der
Stichprobe dadurch auch dann Wahrscheinlichkeitsaussagen machen, wenn man
über die Häufigkeitsverteilung der zugrunde liegenden Parameter in der
Grundgesamtheit nichts weiss. Voraussetzung ist allerdings, dass der
Stichprobenumfang ausreichend gross gewählt wurde.
Die Ableitung der Normalverteilung, die Normaldichte, ist symmetrisch, ihre
Zentralwerte sind identisch, und ihre beiden Minima nähern sind
asymptotisch der Abszisse. Man bezeichnet den geometrischen Abstand zwischen
einem der zwei Wendepunkte und dem Maximum der Normaldichte als
Standardabweichung vom Erwartungswert. Durch Angabe ihres ersten und zweiten
Moments kann jede (mehrdimensionale) Normalverteilung/-dichte vollständig
beschrieben werden.
Die mathematische Statistik kennt verschiedene Verteilungsgesetze für
diskrete und stetige Zufallsvariablen. Da in dieser Arbeit ausschliesslich
stetige (oder stetig gemachte) Merkmale betrachtet werden, beschränkt sich
die folgende Übersicht auf die Verteilungsgesetze diesen Typs. Die verbale
Darstellung des Aufbaus der einzelnen Zufallsvariablen wurde dabei an manchen
Stellen mathematisch geringfügig vereinfacht, um das Konstruktionsprinzip
transparenter zu machen.
Wird eine stetige, n-dimensionale und normalverteilte Zufallsvariable
quadriert, so ist die resultierende Zufallsgrösse
Chi-Quadrat-verteilt mit n Freiheitsgraden. Eine Zufallsvariable, die
sich aus einer stetigen normalverteilten Variable und der Wurzel einer
Chi-Quadrat-verteilten Zufallsvariablen mit n Freiheitsgraden als
Quotient berechnet, ist t-verteilt mit n Freiheitsgraden. Der
Quotient einer Zufallsvariable, der aus zwei Chi-Quadrat-verteilten
Zufallsvariablen mit n und m Freiheitsgraden gebildet wird,
ist F-verteilt mit n Zähler- und m
Nenner-Freiheitsgraden. Im Gegensatz zu den bisher beschrieben Zufallsvariablen
sind gleichverteilte Zufallsvariablen nicht asymptotisch normalverteilt.
Innerhalb eines offenen Intervalls besitzen sie eine konstante Dichte, d.h.
einen gleichbleibenden Erwartungswert, und ausserhalb davon eine
Häufigkeit von Null.
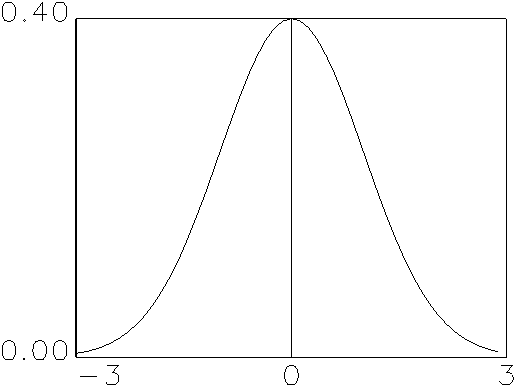
(a) Standardnormaldichte |
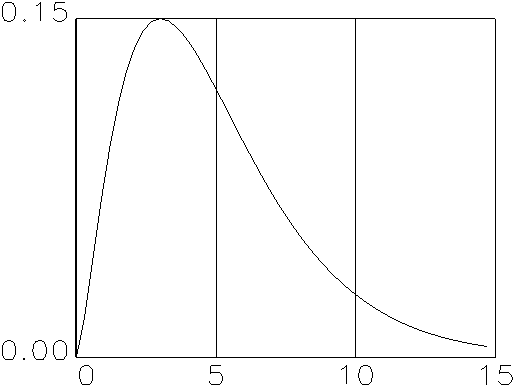
(b) Chi-Quadrat-Dichte mit 5 Freiheitsgraden |
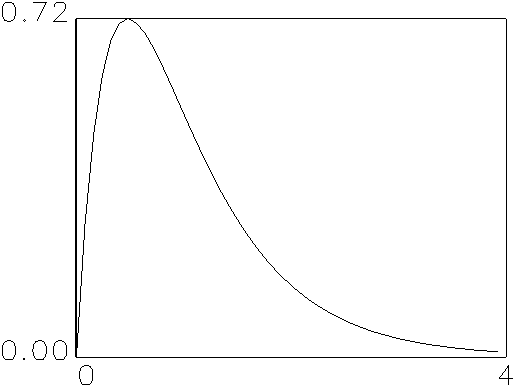
(c) F-Dichte mit 4 Zähler- und 40 Nenner-Freiheitsgraden |
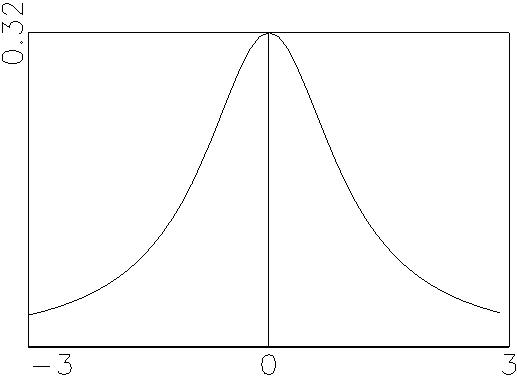
(d) t-Dichte mit 3 Freiheitsgraden |

(e) Histogramm einer Gleichverteilung (aus optischen Gründen diskret dargestellt)
Abbildung 2.5: Verschiedene stetige Dichten.
Quelle: Angelehnt an Bleymüller et al. (1988), S. 61 ff.
Leitet man die Verteilung einer stetigen Variable ab, so erhält man ihre
Dichte. Umgedreht kann durch Integration der Dichte jederzeit die Verteilung
einer stetigen Variable bestimmt werden. Abbildung 2.5 zeigt verschiedene
stetige Dichten.
Die induktive Schlussweise ist mit Unsicherheit behaftet, da die Stichprobe
(ausser im Fall einer Totalerhebung) nur einen Teil der Grundgesamtheit
überdeckt. Ihre Aussagen sind Wahrscheinlichkeitsaussagen. Aufgrund der
Stichprobenergebnisse kann man jedoch die unbekannten Parameter der
Wahrscheinlichkeitsverteilung in der Grundgesamtheit schätzen. Bei der
Punktschätzung wird hierzu aus einer Reihe von Schätzfunktionen
diejenige gewählt, die den besten Schätzwert für einen gesuchten
Parameter liefert. Eine Schätzfunktion ist erwartungstreu, wenn ihr
Erwartungswert mit dem wahren Parameter übereinstimmt. Sie gilt als umso
effizienter, je kleiner ihre Varianz ist. Als konsistent wird sie bezeichnet,
wenn sie wenigstens asymptotisch erwartungstreu ist und ihre Varianz
asymptotisch verschwindet. Zur Konstruktion von Schätzfunktionen mit
wünschenswerten Eigenschaften existieren in der Statistik verschiedene
Verfahren, zum Beispiel die sogenannte Maximum-Likelihood-Methode, die in
Abschnitt 3.2.3 behandelt wird.
Wahrscheinlichkeitsaussagen über die unbekannten Parameter einer
Grundgesamtheit lassen sich auch mithilfe einer Intervall-Schätzung
machen. Bei dieser Vorgehensweise wird ein Vertrauensintervall
(Konfidenzintervall) bestimmt, innerhalb dessen Grenzen ein betrachteter
Parameter mit einer vorher zu definierenden Sicherheit liegt. Die Genauigkeit
der Schätzung ist durch die Breite des Vertrauensintervalls
ausgedrückt.
Unter einer statistischen Hypothese versteht man Annahmen über die Form
der Wahrscheinlichkeitsverteilung eines Parameters in der Grundgesamtheit. Als
statistischen Test bezeichnet man eine Vorschrift, die Bedingungen angibt,
unter denen eine aufgestellte Hypothese abgelehnt werden muss
beziehungsweise nicht abgelehnt werden kann. Die durch eine Stichprobe auf
ihren Wahrheitsgehalt zu prüfende Hypothese nennt man Nullhypothese, und
die zu ihr logische Alternative nennt man Alternativhypothese.
Man unterscheidet in der Statistik zwei Arten von Tests. Der Parametertest
prüft eine Hypothese, die einen Wert(ebereich) für den betrachteten
Parameter festlegt. Durch die unterstellte theoretische Verteilung des
Parameters lässt sich ein kritischer Bereich definieren, innerhalb
dessen die empirische Prüfgrösse des Parameters als signifikant
abweichend von der Nullhypothese gilt. Beim Anpassungstest wird dagegen die
Nullhypothese geprüft, dass die Verteilung des unbekannten Parameters
in der Grundgesamtheit einer bestimmten theoretischen Verteilung entspricht,
etwa der Normalverteilung. Eine praktische Anwendung für diese
statistischen Methoden ist in Abschnitt 3.2.4 beschrieben.
In der Statistik und Ökonometrie arbeitet man mit drei Klassen von Modellen, die
alle dem Zweck dienen, einen vermuteten (funktionalen) Zusammenhang zwischen den
betrachteten Variablen abzubilden. Es sind dies zum einen parametrische Modelle, bei
denen dem gesuchten Zusammenhang eine bestimmte funktionale Form unterstellt wird, so
dass nur noch die Parameter dieser Funktion gefunden werden müssen. Wie in
Abschnitt 2.3 dargelegt wird, lässt sich die Approximation dabei als
Zufallsvariable interpretieren, wodurch ihre Parameter durch eine Punktschätzung
bestimmt werden können. Zum anderen werden nichtparametrische Modelle eingesetzt,
bei denen sich die Annäherung an die wahre Funktion alleine durch Anwendung von
Glättungsverfahren auf die zur Verfügung stehenden Beobachtungen ergibt.
Eine grösser werdende Stichprobe erhöht die Güte der
Approximation. Nichtparametrische Modelle eignen sich vor allem dann, wenn man
keine oder nur unzureichende Kenntnisse hinsichtlich der Struktur des gesuchten
Zusammenhangs besitzt. Es werden daneben auch semiparametrische Modelle
diskutiert, die eine Mischform aus parametrischen und nicht-parametrischen
Modellen darstellen.