Diplomarbeit - Konstruktion von NN für Regressionsanalysen - Kapitel 2.3

---

2.3 Neurometrie - ein synthetischer Ansatz

In Abschnitt 2.1 wurden neuronale Netzwerke als Systeme dargestellt, die sich aus relativ wenig verschiedenen, aber vielfältig kombinierbaren Bestandteilen zusammensetzen. Die sich ergebende Flexibilität in Struktur und Arbeitsweise legt nahe, sie nicht nach allgemeingültigen Prinzipien, sondern problemspezifisch zu konstruieren. Die Approximation unbekannter (funktionaler) Zusammenhänge zwischen Variablen wurde in Abschnitt 2.2 als das Hauptproblem der Ökonometrie herausgestellt. Ob sich neben den beschriebenen statistischen Methoden auch neuronale Netzwerke für die Approximation einsetzen lassen, wird im folgenden Abschnitt untersucht.

2.3.1 Approximation mit neuronalen Netzwerken

Durch die wissenschaftlichen Literatur wurde die Fähigkeiten neuronaler Netzwerke zur Approximation von beliebigen Funktionen mathematisch etabliert. Gallant/White (1988) demonstrierten, dass vorwärtsgekoppelte neuronale Netzwerke mit einer versteckten Schicht und einer Kosinus-Aktivierungsfunktion in der Lage sind, zu jeder Funktion den Wert der zugehörigen Fourierreihe als Ausgabesignal zu liefern. Eine Verallgemeinerung dieses Ansatzes gelang Hornik et al. (1989): Sie ordneten vorwärtsgekoppelte neuronale Netzwerke mit einer versteckten Schicht und sigmoider Aktivierungsfunktion in die Klasse der universellen Approximatoren ein, indem sie bewiesen, dass sich bei Verwendung unendlich vieler versteckter Neuronen jede beliebige Funktion mit der gewünschten Genauigkeit abbilden lässt. Die Ähnlichkeit zwischen Nadaraya-Watson-Kernschätzungsmodellen und neuronalen Netzwerken, die eine radiale Basisfunktion wie zum Beispiel die Gausssche Glockenkurve als Aktivierungsfunktion verwenden, wurde von Poggio/Girosi (1990) dargelegt. Auch Sarle (1994a) und Kuan/White (1994) zeigten, dass verschiedene statistische Methoden zur Approximation von unbekannten Zusammenhängen zwischen Variablen ebenso als neuronale Netzwerke implementiert werden können.

Die allgemeine Verwandtschaft zwischen neuronalen Netzwerken und statistischen Methoden wird in der wissenschaftlichen Literatur immer wieder auch durch Arbeiten mit interdisziplinärem Charakter verdeutlicht. Gish (1992) trainierte beispielsweise die Gewichte seines neuronalen Netzwerks mithilfe der in Abschnitt 3.2.3 beschriebenen Maximum-Likelihood-Methode, um ein binäres Klassifizierungsproblem zu bearbeiten. Das in der Statistik bekannte und hier im Folgenden erläuterte Bias-Varianz-Dilemma wurde von Geman et al. (1992) im Zusammenhang mit neuronalen Netzwerken diskutiert. Azoff (1994) beschrieb neuronale Netzwerke im Kontext herkömmlicher statistischer Methoden kurz als multivariate nichtlineare nichtparametrische Inferenztechniken, die sich insbesondere zur Analyse von Zeitreihen eignen. Eine deutschsprachige Einführung in die Statistik neuronaler Netzwerke wurde von Arminger (1994) gegeben. Kuan/White (1994) haben einen Literaturüberblick über aktuelle Forschungsergebnisse zusammengestellt. Auch von Cheng/Titterington (1994) werden neuronale Netzwerke aus einer statistischen Perspektive betrachtet und diskutiert. Die Veröffentlichungen von Anders (1995) sowie Anders/Korn (1996) beschreiben schliesslich die theoretischen Grundlagen und potenziellen Einsatzmöglichkeiten von neuronalen Netzwerken zur Approximation unbekannter Zusammenhänge zwischen Variablen unter statistischen Gesichtspunkten in einer Weise, an die die vorliegende Arbeit direkt anknüpfen kann.

Neuronales Netzwerk	(Nicht-)Parametrisches Modell
Topologie	Spezifikation
Ungeeignete Topologie	Über- oder Unterparametrisierung
Aktivierungsfunktion	Transformationsfunktion
Muster	Beobachtung
Inputs	Unabhängige (erklärende) Variablen
Output	Abhängige (zu erklärende) Variablen
Gewichte	Parameter (Regressionskoeffizienten)
Training	Schätzung
Trainingsmenge	in sample-Menge
Validierungsmenge	out of sample-Menge
Konvergenz	in sample-Qualität
Generalisierung	out of sample-Qualität
Klassifizierung	Diskriminanzanalyse
Überwachte Lernverfahren	Regression, Approximation
Soll-Ist-Abweichung	Residuen
Rauschen	Unsystematischer Fehler
Epoche	Numerischer Iterationsprozess

Tabelle 2.1: Vergleich der Terminologien.
Quelle: Angelehnt an Sarle (1994b).

Ohne an dieser Stelle die Begriffe der Tabelle 2.1 erläutern zu können, wird durch die Gegenüberstellung deutlich, dass die Verwandtschaft zwischen neuronalen Netzwerken und statistischen Methoden zum Teil nur durch die Verwendung einer unterschiedlichen Terminologie verschleiert wird. Die von de Groot (1993) geäusserte Kritik an der aktuellen Forschung bleibt jedoch trotz Kenntnis dieses Sachverhalts bestehen: "However, the method is still under development, being more like a heuristic framework rather than a statistical theory [...]"

2.3.2 Regressionsmodelle und neuronale Netzwerke

Es wurde in Abschnitt 2.2 bereits angedeutet, dass Regressionsmodelle das derzeit gebräuchlichste Instrument der Ökonometrie sind, um Beziehungen zwischen Variablen aufdecken und darstellen zu können. Wie oben beschrieben wurde, hat die Forschung inzwischen formal bewiesen, dass mehrschichtige, vorwärtsgekoppelte neuronale Netzwerken mit sigmoiden Aktivierungsfunktionen ebenfalls für diese Aufgabe heranziehbar sind. Dies legt einen Vergleich der beiden Vorgehensweisen nahe.

Ein Regressionsmodell liefert Ergebnisse zurück, die es ermöglichen, die Abhängigkeiten zwischen Variablen in mathematischer Form zu beschreiben. Im Modell der Einfachregression wird zum Beispiel angenommen, dass eine Variable Y von einer zweiten Variable X abhängig ist. Mithilfe der durch die Regression ermittelten Regressionsfunktion können aus den Werten der unabhängigen Variablen X Aussagen über die zugehörigen Werte der abhängigen Variable Y abgeleitet werden. Der Verlauf der Regressionsfunktion ist durch ihre Parameter (Korrelationskoeffizienten) determiniert, die die Beobachtungen der Eingabevariablen in spezifischer Weise gewichten. In den herkömmlichen Regressionsmodellen werden diese Parameter durch die Methode der kleinsten Quadrate bestimmt, indem die Summe der quadrierten Abweichungen zwischen den Werten der Regressionsfunktion und den Werten der Y-Variable minimiert wird. Durch Streuungsdiagramme, bei denen die Beobachtungen der Variable X und die Beobachtungen der Variable Y als Wertepaare in das kanonische Koordinatensystem eingetragen werden, kann dieser Sachverhalt grafisch dargestellt werden (vergleiche Abbildung 2.6 und Abbildung 2.7).

(a) Alternative Regressionsgeraden

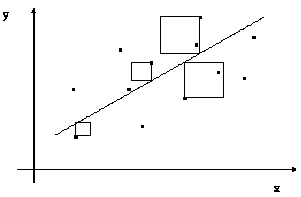
(b) Nach der Methode der kleinsten Quadrate entwickelte Regressionsgerade

Abbildung 2.6: XY-Streuungsdiagramme mit Regressionsgerade(n) durch eine Punktewolke.
Quelle: Angelehnt an Bleymüller et al. (1988), S. 140.

(a) Kein Zusammenhang zwischen X und Y

(b) Linearer Zusammenhang zwischen X und Y

(c) Nichtlinearer Zusammenhang zwischen X und Y

Abbildung 2.7: XY-Streuungsdiagramme mit Regressionsfunktion.
Quelle: Angelehnt an Bleymüller (1988), S. 139.

Wie man anhand der obigen Beispiele erkennen kann, erfasst die Regressionsfunktion nicht unbedingt alle beobachteten Wertepaare, sondern gibt nur die Grundtendenz des Zusammenhangs wieder. Eine Regressionsgerade ohne Steigung lässt vermuten, dass kein Zusammenhang zwischen den betrachteten Variablen besteht (Abbildung 2.7a). Abbildung 2.7b weist dagegen auf einen linearen Zusammenhang zwischen den Variablen hin: Je grösser X ist, desto grösser ist auch Y. In Abbildung 2.7c ist ein Beispiel für einen nichtlinearen Zusammenhang zwischen X und Y gegeben.

Im folgenden wird die Stellung neuronaler Netzwerke im Kontext der herkömmlichen statistischen Modelle erörtert. Dieser Teil der Arbeit stützt sich - wie in der Einleitung erwähnt - auf die theoretischen Untersuchungen von Anders (1995). Hier erfolgt die Darstellung jedoch in stärker verbalisierter und visualisierten Form, um die Intention hinter dieser Analyse für das Verständnis von Kapitel 3 hervorzuheben.

Man bezeichnet die Abweichungen zwischen den Beobachtungspunkten und den zugehörigen Regressionspunkten als Residuen, die quadrierte Summe aller Residuen als Sum of Squared Errors (SSE) und die gemittelte Summe aller quadrierten Residuen als Mean Squared Error (MSE). Durch mathematische Umformungen lässt sich der MSE in zwei Komponenten zerlegen, die als systematischer Fehler (Approximationsfehler) und als unsystematischer Fehler (Störterm) bezeichnet werden. Abbildung 2.8 zeigt die Zerlegung der zu erklärenden Einzelabweichungen, die sich durch Anwendung der Methode der kleinsten Quadrate ergibt, wobei x_i die i-te Beobachtung der unabhängigen Variable, y_i die i-te Beobachtung der abhängigen Variable, y_mu das arithmetische Mittel von y und yh_i den durch die Regressionsfunktion ermittelten Schätzwert für y_i darstellt.

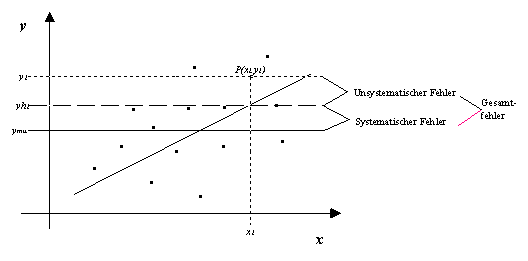
Abbildung 2.8: Zerlegung der zu erklärenden Einzelabweichungen.
Quelle: Angelehnt an Greene (1993), S. 148.

Die Güte einer Regression wird alleine mit dem Approximationsfehler gemessen, denn der Störterm ist rein zufälliger Natur und damit durch kein (Regressions-)Modell zu erklären. Interpretiert man darüber hinaus die abhängige Variablen als Zufallsvariable und die Regressionsfunktion als Schätzfunktion für die wahre Funktion, dann kann der Approximationsfehler dahin gehend aufgeschlüsselt werden, dass er sich aus der Summe des quadrierten Bias und der Varianz der Schätzfunktion zusammensetzt. Abbildung 2.9 verdeutlicht diesen Zusammenhang: Eine optimale Schätzfunktion würde die wahre Funktion ohne Bias und mit der kleinst möglichen Varianz approximieren.

Abbildung 2.9: Bias und Standardabweichung einer Schätzfunktion.
Quelle: Angelehnt an Anders (1995), S. 7.

Eine Theorie der statistischen Forschung besagt, dass unterparametrisierte Modelle generell keine erwartungstreuen Schätzfunktionen liefern können. Nichtparametrische Modelle hingegen bringen zwar biasfreie, aber mit hoher Varianz behaftete Schätzfunktionen hervor. Daraus lässt sich ableiten, dass man den Approximationsfehler der statistischen Modelle niemals bezüglich des Bias als auch der Varianz a priori ausschliessen kann. Geman et al. (1992) nennen dieses Dilemma das Bias-Varianz-Dilemma. Durch Vorgabe der zu modellierenden Struktur des gesuchten Zusammenhangs wird daher immer ein Kompromiss zwischen den beiden Komponenten des Approximationsfehlers getroffen. Die in Abbildung 2.10a gezeigte Schätzfunktion besitzt beispielsweise einen kleineren Bias, aber eine grössere Varianz als die in Abbildung 2.10b gezeigte Schätzfunktion, wobei sich die jeweils zugrunde liegenden linearen Regressionsmodelle in der Anzahl ihrer Eingabevariablen (und damit auch in der Anzahl ihrer Parameter) unterscheiden.

(a) Schätzfunktion mit Bias und Varianz

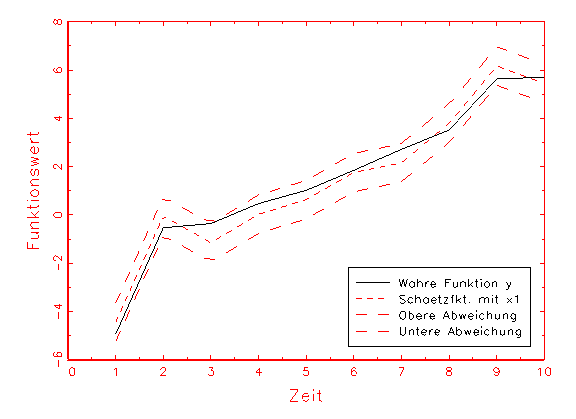
(b) Schätzfunktion mit etwas grösserem Bias, aber deutlich kleinerer Varianz als (a)

Abbildung 2.10: Kompromiss zwischen Bias und Varianz.
Die Grafiken wurden mit Neurometricus (vergleiche Abschnitt 3.1) erstellt.

Herkömmliche Regressionsmodelle sind parametrisch, d.h zur Bildung einer Regressionsfunktion muss dem gesuchten Zusammenhang zwischen den Variablen eine bestimmte funktionale Form unterstellt werden. In der Praxis bedeutet das, dass der Anwender die nötige Struktur der Regressionsfunktion im voraus "erahnen" muss. Wird zum Beispiel eine nichtlineare Abhängigkeit zwischen den Variablen vermutet, dann kann man auf ein Polynom höherer Ordnung als mögliche Regressionsfunktion zurückgreifen. Nicht jedes nichtlineare Problem ist jedoch polynomialer Natur. Wendet man dennoch diese Klasse von Funktionen an, so sind in der Regel übermässig viele Parameter zu allokieren, was - wie oben gezeigt wurde - eine Steigerung der Varianz der Schätzfunktion zur Folge hat.

Neuronale Netzwerke können, da sie der Klasse der universellen Approximatoren angehören, im Prinzip als nichtparametrische Modelle interpretiert werden. Nach Spezifizierung ihrer Modellparameter sind sie jedoch formal als parametrische Modelle anzusehen, denn ihnen wird implizit unterstellt, dass sie in der Lage sind, den gesuchten Zusammenhang zu approximieren. Neuronale Netzwerke präsentieren sich demnach als eine neuartige Klasse von statistischen Methoden, die sich im Gegensatz zu parametrischen und nicht-parametrischen Modellen frei auf dem in Abbildung 2.11 gezeigten Kontinuum bewegen können.

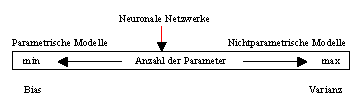
Abbildung 2.11: Kontinuum zwischen parametrischen und nicht-parametrischen Modellen.
Quelle: Angelehnt an Anders (1995), S. 8.

Aus den oben gemachten Ausführungen lässt sich - obgleich nur intuitiv - ableiten, dass mit neuronalen Netzwerken Regressionsmodelle grundsätzlich simuliert werden können. Auf einen formalen Beweis dieser Behauptung sei an dieser Stelle verzichtet. In Abbildung 2.12 findet der Leser stattdessen einige neuronale Netzwerkarchitekturen, unter denen jeweils die mathematische Gleichung der zugehörigen Regressionsfunktion angegeben ist.

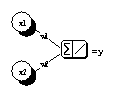
y=x1×w1+x2×w2

(a) Lineares Modell

y=g(x1× w1+x2× w3)× w5+g(x1× w2+x2× w4)× w6

(b) Nichtlineares Modell

y=g(x1× w1+x2× w2)× w3+x1× w4+x2× w5

(c) Erweitertes Modell

Abbildung 2.12: Neuronale Regressionsmodelle. Das g in den mathematischen
Gleichungen steht für eine beliebige nichtlineare Aktivierungsfunktion.
Quelle: Angelehnt an Anders (1995), S. 11.

Die Fähigkeiten und Grenzen dessen, was Regressionsmodelle zu leisten vermögen, sind gut erforscht. Jedoch sind nicht alle statistischen Methoden, die für parametrische Modelle gelten, auch auf neuronale Netzwerke anwendbar. Wie in Kapitel 3 anhand praktischer Beispiele demonstriert wird, liefert die Statistik dennoch eine Fülle von neuen Werkzeugen, die bei der Konstruktion und der Diagnose der Ergebnisse von neuronalen Netzwerken bisher keine oder nur eine formal unbegründete Verwendung gefunden haben. Im Übrigen wird der Einsatz von statistischen Methoden durch wohlbekannte Annahmenkataloge reglementiert, die asymptotisch gültige Ergebnisse garantieren. So können zum Beispiel alle Regressionsfunktionen, die auf der Methode der kleinsten Quadrate basieren, nur dann Gültigkeit für sich beanspruchen, wenn die im Folgenden aufgeführten Modellannahmen gelten.

1. Das Modell kann den gesuchten Zusammenhang zwischen den Variablen zumindest theoretisch approximieren.
2. Der Störterm besitzt einen Erwartungswert von Null.
3. Der Störterm ist homoskedastisch, d.h. seine Varianz ist für alle Beobachtungen konstant.
4. Der Störterm ist nicht autokorreliert, d.h. es herrscht keine Kovarianz zwischen den Beobachtungen.
5. Der Störterm korreliert nicht mit den unabhängigen Variablen.
6. Der Störterm ist normalverteilt.

Zusammenfassend lässt sich festhalten, dass neuronale Netzwerke im Kontext ökonometrischer Methoden gesehen werden können und deren Potenzial nicht unbeträchtlich erweitern. Anders (1995) attribuiert diese Perspektive mit neurometrisch. Durch diese Sichtweise wird auch deutlich, dass jener Ansatz nicht länger haltbar ist, der neuronale Netzwerke generell als Black-Boxes begreift, in die bedenkenlos Daten eingespeist werden dürfen, da sie die Qualität der Daten aufgrund ihrer "Intelligenz" eigenständig beurteilen könnten. Solchen Ansprüchen können sie nicht gerecht werden, aber es weckt beim Laien überzogene Hoffnungen, die zu der vielfach kritisierten Mythologisierung der Fähigkeit von neuronalen Netzwerken beigetragen haben.

2.3.3 Beispiele

Nachdem deutlich geworden ist, dass neuronale Netzwerke theoretisch gesehen nichts anderes sind als eine Oberklasse der Regressionsmodelle, wird dieser Anspruch noch anhand einiger Beispiele aus der Praxis erhärtet, die in den letzten Jahren in der wissenschaftlichen Literatur vorgestellt wurden.

Eine der ersten Untersuchungen, die neuronale Netzwerke zur Analyse von nichtlinearen Prozessen verwendete, wurde von Lapedes/Farber (1987) veröffentlicht. Eine tiefer gehende statistische Analyse der Ergebnisse fehlte hier aber. Das beobachtete Chaos in der Entwicklung der Marktpreise regte gleich vier Forscher zu einer neurometrischen Schätzung an: Casdagli (1989), Vaga (1990), Larrain (1991) und Peters (1991). In der Dissertationsschrift von de Groot (1993) wurden die Ergebnisse einer Zeitreihenanalyse mithilfe der in Abschnitt 2.2 vorgestellten statistischen Methoden diagnostiziert. Geliefert wurden sie von einem dreischichtigen, vorwärtsgekoppelten neuronalem Netzwerk mit einer Tangens Hyperbolicus-Aktivierungsfunktion, die auch die in dieser Arbeit favorisierte Aktivierungsfunktion ist (vergleiche Kapitel 3). Zuletzt sei noch eine Untersuchung von Refenes (1993) erwähnt, der ein neuronales Netzwerk mit 35 Neuronen über ein Jahr lang mit den stündlichen Wechselkursen trainierte, um auf diese Weise ökonomisch interessante Prognosedaten zu gewinnen.

Die obige Liste ist keineswegs vollständig. Es liessen sich leicht Beispiele finden, in denen neuronale Netzwerke zur Approximation von Funktionen herangezogen wurden. Aber die meisten Veröffentlichungen behandeln ausschliesslich binäre Probleme, während in der Ökonometrie auch reelwertige Zeitreihen relevant sind. Teilaspekte der aufgezeigten Zusammenhänge zwischen neuronalen Netzwerken und statistischen Methoden werden ebenfalls relativ häufig aufgeführt, meist aber nur theoretisch und nicht praktisch bedacht. Eine neurometrische Analyse von empirischen Daten in einer ähnlich umfassenden Form wie sie in Abschnitt 3.3 durchgeführt wird, hat der Verfasser nicht gefunden.