Diplomarbeit - Konstruktion von NN für Regressionsanalysen - Kapitel 3.2
von Daniel Schwamm (09.11.2000)
Bei der Analyse in Kapitel 2 hat sich ergeben, dass neuronale Netzwerke
als Modelle interpretiert werden können, die auf einem Kontinuum zwischen
parametrischen und nichtparametrischen Modellen liegen. Des Weiteren wurde
ausgeführt, dass durch Variation der Anzahl der Parameter des
neuronalen Netzwerks ein Kompromiss zwischen Bias und Varianz gefunden
werden kann. Mit diesem Zielansatz wird hier ein allgemeiner Prozess zur
problemspezifischen Konstruktion von neuronalen Netzwerken eingesetzt
(neurometrischer Modellbildungsprozess; vergleiche Abbildung 3.1). Seine
Vorgehensweise orientiert sich an dem klassischen Konzept der Modellbildung
für statistische Schätzungen, wie es Box und Jenkins (1976)
vorgeschlagen haben.

Abbildung 3.1: Neurometrischer Modellbildungsprozess.
Quelle: Angelehnt an Anders (1995), S. 27.
Die vier Hauptschritte des neurometrischen Modellbildungsprozesses -
Identifikation, Spezifikation, Schätzung und Diagnose - werden bei
Neurometricus durch ein oder mehrere Module repräsentiert. Thema der
nächsten Abschnitte wird die Funktionalität sein, die die Module dem
Anwender in jedem Modellierungsschritt anbieten. Die Beschreibung erfolgt
weitgehend in der statistischen Terminologie, da diese im Rahmen der
vorliegenden Arbeit eine Obermenge der neuroinformatischen Terminologie
darstellt.
Probleme, die im Zusammenhang mit Regressionsmodellen auftreten, müssen
bei neuronalen Netzwerken ebenfalls beachtet werden (vergleiche Abschnitt 2.3).
Da zum Beispiel beide Modelle auf mathematischen Gleichungen basieren, die
einen hohen Komplexitätsgrad annehmen können, reagieren ihre
Ergebnisse im hohem Masse empfindlich auf Fehler in den Eingabevariablen.
Um diesem als Konditionsproblem bezeichneten Phänomen entgegenzuwirken,
ist das zur Verfügung stehende Datenmaterial zu selektieren und einer
genauen Analyse zu unterziehen.
Zum Austesten des Verhaltens von statistischen Modellen lassen sich sogenannte
Designmatrizen bilden, die Eingabevariablen enthalten, die vom Prüfer
deterministisch vorgegeben werden. Die Auswahl der Daten ist in diesem Fall
unproblematisch. Bei der Verwendung empirischer Daten treten jedoch zahlreiche
kritische Situationen auf, wie die folgende - unvollständige -
Aufzählung zeigt:
-
Multikollinearität: Die unabhängigen Variablen korrelieren zu
stark, um eine Analyse ihrer individuellen Effekte zu erlauben.
-
Fehlende Beobachtungen: Die Ausprägungen einer Variable können
nicht immer zu allen Zeitpunkten erhoben werden. In diesem Fall wird bisweilen
versucht, den fehlenden Wert künstlich zu berechnen, was wiederum andere
Fehlerquellen birgt.
-
Gruppierte Daten: In der Statistik muss man häufig auf
gruppierte Durchschnittswerte einer Variablen zurückgreifen, da nicht
immer Einzelbeobachtungen möglich sind. Dadurch wird die Realität
jedoch bis zu einem gewissen Grad verzerrt wiedergeben.
-
Messfehler: Jede Messung der Ausprägung einer (stetigen)
Variable ist fehlerbehaftet. In den statistischen Modellen findet dieser
Umstand durch die Einführung von Störtermen Berücksichtigung,
denen man jedoch gewisse Annahmen unterstellen muss, die nicht immer
erfüllt sind (vergleiche Abschnitt 2.3).
-
Stetige Variablen: Zeitreihen sind natürlicherweise stetig. Aus
ihnen sind diskrete Zeitreihen erst zu entwickeln. Dazu wird ein
Sample-Schema benutzt, welches die Zeit in gleiche Intervalle einteilt.
Die Intervallgrösse ist aber meist nicht frei von menschlicher
Willkür.
-
Indikatoren: Sind Variablen unmessbar geartet, so werden
stattdessen ihre Indikatoren erhoben. Dadurch werden aber
gezwungenermassen nur Teilaspekte der Realität der Variablen
berücksichtigt.
-
Ausreisser: (Stochastische) Variablen unterliegen bisweilen
Schwankungen, die ihrem natürlichem Verhalten zuwiderlaufen. Dies
konkretisiert sich in Ausreissern, die vor einer Schätzung nach
Möglichkeit auszufiltern sind.
-
Nichtstationarität: (Stochastische) nichtstationäre Variablen
schwanken um keinen Gleichgewichtszustand. In diesem Fall wird den Variablen
durch sogenannte Schocks ein Trend vermittelt, der im Lauf der Zeit nicht
verloren geht. Dies bedingt Ausreisser in den Residuen einer
Schätzung.
In der statistischen Literatur werden verschiedene Verfahren erörtert, um
die oben genannten Datenprobleme zu mildern oder ganz zu verhindern. Die
Diskussion fällt zum Teil kontrovers aus. Azoff (1994) schlägt zum
Beispiel vor, fehlende Beobachtungen durch Interpolation der vorhandenen
Beobachtung zu gewinnen, während Greene (1993) darauf hinweist, dass
sich in Monte-Carlo-Studien abgezeichnet hat, dass diese Vorgehensweise
eher aufwendig als vorteilhaft ist. Es existieren jedoch allgemein anerkannte
Methoden, um Probleme in den Daten vor beziehungsweise nach einer
Schätzung zu erkennen und zu beheben. Einige von ihnen sind als Funktionen
in den Datenidentifikations-Modulen von Neurometricus integriert worden und
werden im Folgenden beschrieben.
Um sich über die Qualität des zur Verfügung stehenden
Datenmaterials zu informieren, kann man sich von Neurometricus wichtige
Statistiken (Median, Maximum, Summe, Schiefe, ...) der zur Verfügung
stehenden Variablen berechnen lassen. Eine grafische Analyse, die sich daran
anschliesst, hilft dem Anwender ebenfalls bei der Identifikation von
etwaigen Datenproblemen. Das Zeitreihen-Diagramm in Abbildung 3.2a zeigt
beispielsweise eine Variable, die ab der 50. Beobachtung nicht mehr um Null
streut, d.h. nichtstationär wird. In Abbildung 3.2b ist ein
XY-Streuungs-Diagramm zu sehen, welches verdeutlicht, dass 5
Ausreisser bei 100 Beobachtungen genügen, um die lineare
Regressionsgerade zu verzerren. Anhand des in Abbildung 3.2c gegebenen
Histogramms erkennt man, dass die betrachtete Variable nicht
normalverteilt ist und Ausreisser besitzt.
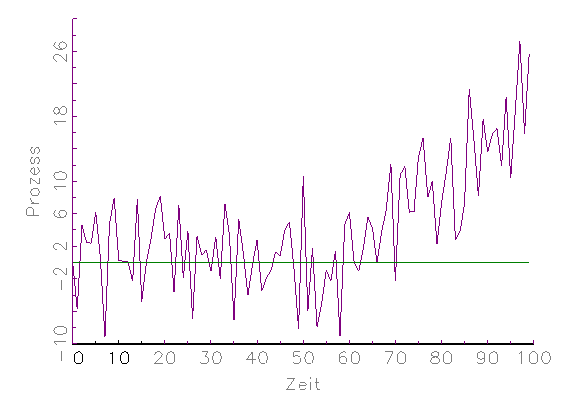
(a) Zeitreihen-Diagramm
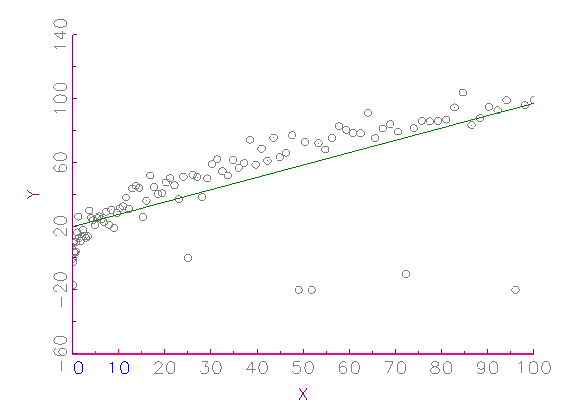
(b) XY-Streuungs-Diagramm mit Regressionsgerade
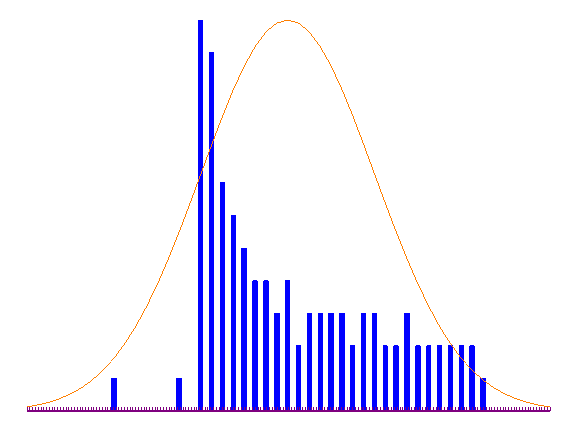
(c) Histogramm
Abbildung 3.2: Grafische deskriptive Analyse der Daten.
Nichtstationäre Prozesse können auf relativ einfache Weise durch
sogenannte Differenzfilter erster (oder höherer) Ordnung in
stationäre Prozesse transformiert werden, deren Momente invariant sind,
und deren durch Schocks verursachte Trends asymptotisch verschwinden. Dadurch
wird verhindert, dass sich gute Approximationen zwischen zwei Variablen
alleine aufgrund eines gemeinsamen Zeittrends ergeben.
Ausreisser kann man beseitigen, indem man zum Beispiel nur diejenigen
Beobachtungen zulässt, die sich innerhalb der Standardabweichung
bewegen, oder indem man die Daten nichtlinear in ein beschränktes
Intervall transformiert (Glättung der Daten). Besitzt man vergleichbare
Zeitreihen früherer Erhebungen, so kann man die Ausreisser eventuell
auch durch dazu adäquate Werte ersetzen.
Zeigt eine Variable nicht die gewünschte Verteilung, so kann sie unter
Umständen durch Bildung neuer Klassen oder Hinzunahme zusätzlicher
Effekte nachträglich dahin gehend angepasst werden. In einigen
Untersuchungen hat es sich beispielsweise als vorteilhaft erwiesen, die
abhängigen Variablen mit einem künstlichen Störterm zu versehen,
der die für ein Regressionsmodell nötigen Bedingungen erfüllt
(vergleiche Abschnitt 2.3).
Annähernde lineare Abhängigkeiten (Kollinearitäten) zwischen
unabhängigen Variablen sind vor einer Schätzung zu verhindern, da sie
sich negativ auf die Stabilität ihrer Ergebnisse auswirken. Typische
Symptome der (Multi-)Kollinearität sind zum Beispiel signifikante, aber
mit unglaubwürdig grossen Standardabweichungen versehene Parameter.
Im Fall von exakter linearer Abhängigkeit ist aus mathematischen
Gründen überhaupt keine Schätzung möglich; die
Kovarianzmatrix der unabhängigen Variablen ist dann singulär
Neurometricus beinhaltet mehrere Verfahren, mit denen Kollinearität
zwischen den unabhängigen Variablen festgestellt werden kann. Aus
Platzgründen werden hier nur die Methoden der Eigenwertberechnung und der
grafischen Kollinearitätsanalyse vorgestellt.
Die Korrelationsmatrix wird aus den Beobachtungen der unabhängigen
Variablen
gebildet. Ihre Komponenten beschreiben, wie stark die Variablen untereinander
zusammenhängen. Positive Korrelation zwischen der Variable x1 und
der Variable x2 ist zum Beispiel gegeben, wenn bei grösser
beziehungsweise kleiner werdenden Werten von x1 auch tendenziell
grösser beziehungsweise kleiner werdende Werte von x2
beobachtet werden. Die Eigenvektoren einer Matrix besitzen die Eigenschaft,
dass sie orthogonal zueinander sind. Im Falle der Korrelationsmatrix der
unabhängigen Variablen liefern sie die Richtung der jeweils
grössten Streuung der Beobachtungen der einzelnen Variablen.
Multipliziert man sie mit den zugehörigen Eigenwerten, so
erhält man die Hauptachsen des sogenannten Eigenraums. Da die Eigenwerte
umso grösser ausfallen, je weniger die unabhängigen Variablen
untereinander zusammenhängen, sind sie ein geeignetes Kriterium, um
Kollinearität feststellen zu können.
Bei der grafischen Kollinearitätsanalyse werden zunächst die n
unabhängigen Variablen orthonormalisiert, wodurch ihre
Beobachtungsvektoren
senkrecht zueinanderstehen und eine Länge von Eins besitzen. Auf Basis
der sich
daraus ergebenden Korrelationsmatrix werden im nächsten Schritt die
Hauptachsen
des n-dimensionalen Eigenraums berechnet. In Form von zwei- und
dreidimensionalen
Kollinearitätsanalyse-Schaubildern lassen sich dann jeweils
Untereigenräume grafisch darstellen. Hierbei gilt, dass der
Untereigenraum umso besser aufgespannt wird, je unabhängiger die
beteiligten Variablen voneinander sind. Abbildung 3.3a zeigt zum Beispiel ein
Kollinearitätsanalyse-Schaubild von drei Variablen, die offenbar nicht
korreliert sind, da die Hauptachsen des Eigenraums alle gleichlang sind. Im
Gegensatz dazu ist in Abbildung 3.3b ein Kollinearitätsanalyse-Schaubild
gegeben, dessen Variablen x1 und x2 mit x3 korrelieren,
weswegen die x3-Hauptachse des Eigenraums kaum ausgeprägt ist.
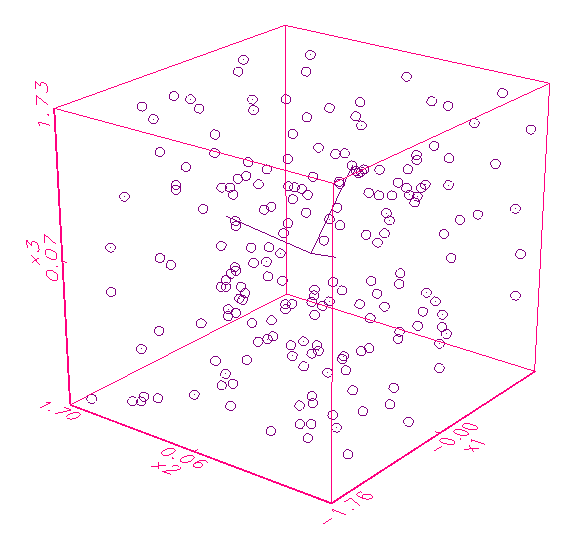
(a) Dreidimensionales Kollinearitätsanalyse-Schaubild
mit voll aufgespanntem Eigenraum
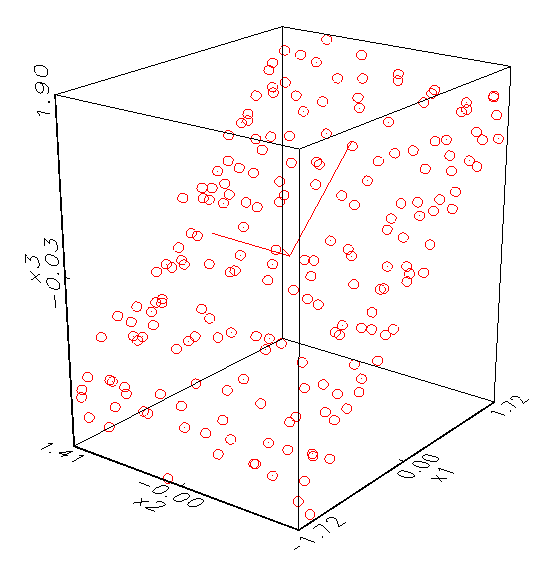
(b) Dreidimensionales Kollinearitätsanalyse-Schaubild
mit annähernd zweidimensionalem Eigenraum
Abbildung 3.3: Grafische Kollinearitätsanalyse der Daten.
Probleme mit Multikollinearität lassen sich unterbinden, indem die am
stärksten korrelierten Variablen von der Betrachtung ausgeschlossen
werden. Durch die Reduzierung der Dimension der Eingabevariablen erhält
man den positiven Nebeneffekt, dass das zu schätzende Modell weniger
Parameter allokiert, wodurch die Varianz der Schätzung abnimmt. Wenn die
Eingabevariable aber nicht zu 100% korreliert ist mit einer anderen
Eingabevariable und einen signifikanten Erklärungsbeitrag zur
Approximation liefern kann, wird durch ihre Entnahme immer auch ein Bias in der
Schätzung verursacht.
Ein neuronales Netzwerk gilt als generalisierungsfähig, wenn mit seiner
Hilfe aus einer ungeschätzten Eingabemenge eine sinnvolle Ausgabemenge
generiert werden kann. Um die Leistungsfähigkeit eines geschätzten
neuronalen Netzwerks unter realen Bedingungen adäquat beurteilen zu
können, muss es mit Beobachtungen überprüft werden, die bei
der Schätzung nicht verwendet wurden. Dieses Testverfahren macht es
erforderlich, dass das zur Verfügung stehende Datenmaterial auf
verschiedene Mengen aufgeteilt wird. In Neurometricus werden insgesamt vier
Mengentypen unterschieden:
-
Trainingsmenge: Die Parameter des neuronalen Netzwerk werden in der
Regel ausschliesslich mithilfe dieser Menge geschätzt. Sie
lässt sich unterteilen in die Eingabe- und Ausgabemenge, deren
Dimension jeweils durch die Anzahl der Eingabe- beziehungsweise
Ausgabevariablen definiert ist. Jede Variable wird durch einen Spaltenvektor
von n Beobachtungen repräsentiert.
-
Validierungsmenge (optional): Um während der Schätzung die
Generalisierungsfähigkeit des neuronalen Netzwerks überprüfen zu
können (und um dadurch gegebenfalls einen Abbruch der Schätzung zu
erwirken), wird diese Menge benötigt. Ihre Grösse, d.h. die
Anzahl der enthaltenen Beobachtungen, kann vom Benutzer bestimmt werden.
Kerling/Poddig (1994) empfehlen 15% der Trainingsmenge.
-
Prüfmenge (optional): Mithilfe der Prüfmenge testet man die
Generalisierungsfähigkeit des neuronalen Netzwerks nach der
Schätzung. Ihre Grösse ist optional; 50% der Trainingsmenge
schlagen Kerling/Poddig (1994) vor.
-
Realmenge (optional): Ist ein neuronales Netzwerk geschätzt und
geprüft, kann es unter Verwendung von empirischem Datenmaterial praktisch
eingesetzt werden. Die Realmenge besteht aus den tatsächlichen
Beobachtungen der Eingabevariablen.
Die Aufteilung der originalen Eingabemenge lässt sich durch die
Funktionen von Neurometricus auf mehrere Arten realisieren. Im folgenden wird
nur die analytische Methode des (erweiterten) Duplex-Verfahrens von
Kennard/Stone (1969) und Snee (1977) vorgestellt.
Das Teilungsverfahren muss sicherstellen, dass die mit ihm gebildeten
Mengen
über ähnliche statistische Eigenschaften verfügen, da den
zugehörigen Variablen implizit eine gemeinsame Grundgesamtheit unterstellt
wird.
Um dieses Ziel zu erreichen, berechnet das Duplex-Verfahren im ersten Schritt
die
euklidischen Distanzen der orthonormalisierten Zeilenvektoren der Matrix, die
die
Beobachtungen der Eingabevariablen bilden. Als Spezialfall der
Minkowski-Q-Metriken beschreiben die euklidischen Distanzen die geometrischen
Abstände der Beobachtungspunkte in einem n-dimensionalen Raum mit
kanonischer Basis. Euklidische Distanzen besitzen die Eigenschaft, dass
sie transformations- und skaleninvariant sind, d.h sie sind
unabhängig von den (verschiedenen) Masseinheiten der Eingabevariablen
und ändern sich nicht durch Drehung/Spiegelung des Koordinatensystems. Aus
ihnen lässt sich eine sogenannte Distanzmatrix generieren, aus der
wiederum sukzessive die am weitesten voneinander entfernten Beobachtungspunkte
bestimmt und auf zwei verschiedene Mengen verteilt werden können. Da die
statistischen Eigenschaften einer Menge vor allem durch ihre Extrema
beeinflusst werden, erfüllt man auf diese Weise das angestrebte Ziel.
Wie beschrieben, muss sichergestellt sein, dass die
Neurometricus-Mengen
derselben Grundgesamtheit entstammen. Das Duplex-Verfahren stellt dies durch
eine
analytisch-deterministische Berechnungen sicher. Neurometricus bietet dem
Anwender
jedoch auch einige stochastische Teilungsverfahren an, deren resultierende
Mengen mit
Hilfe einer einfachen Varianzanalyse auf Ähnlichkeit überprüft
werden
sollten. Bei diesem Verfahren wird die Nullhypothese "die Mengen
verfügen über den gleichen Mittelwert" getestet. Es wird dazu
eine Prüfgrösse berechnet, die hypothetisch F-verteilt ist.
Erfolgt unter dieser Annahme keine signifikante Ablehnung der Nullhypothese, so
können die beteiligten Mengen bzgl. ihres arithmetischen Mittels als aus
der gleichen Grundgesamtheit entstammend angenommen werden. Der Anwender sollte
die Mengenteilung unter Umständen mehrfach wiederholen, bis dieses
Ergebnis erreicht ist. Zu überprüfen sind dabei immer auch die
Annahmen, die die einfache Varianzanalyse voraussetzt, um gültige Aussagen
treffen zu können: Alle betrachteten Variablen müssen normalverteilt
und homoskedastisch sein, d.h. die gleiche Varianz besitzen.
Liegen den Beobachtungen der Eingabevariablen verschiedene Masseinheiten
zugrunde, so kann dies dazu führen, dass die Variablen mit den
grösseren Zahlenwerten unverhältnismässig stark die
Ergebnisse der Schätzung beeinflussen. Solche Skalenvarianz kann auch im
Zusammenhang mit den Aktivierungsfunktionen der Neuronen zu Problemen
führen, selbst wenn deren Definitionsbereich unbegrenzt sein sollte. Bei
Verwendung des Tangens hyperbolicus ist beispielsweise darauf zu achten,
dass diese Funktion für Eingabevariablen mit Beobachtungen kleiner -3
beziehungsweise grösser +3 nur die Werte -1 beziehungsweise 1
zurückliefert. Durch eine Einschränkung des Definitionsbereichs kann
das nichtlineare Transformationspotenzial des Tangens hyperbolicus effizienter
genutzt werden.
Neurometricus bietet dem Anwender derzeit zwei Verfahren an, um multivariate
Eingabemengen auf einen gemeinsamen numerischen Rang zu transformieren: Die
Mittelwert-Varianz-Normierung und die Intervall-Normierung. Ihre jeweilige
Wirkung auf die Variablen kann mit den Zeitreihen-Diagrammen von Neurometricus
grafisch demonstriert werden (vergleiche Abbildung 3.4).
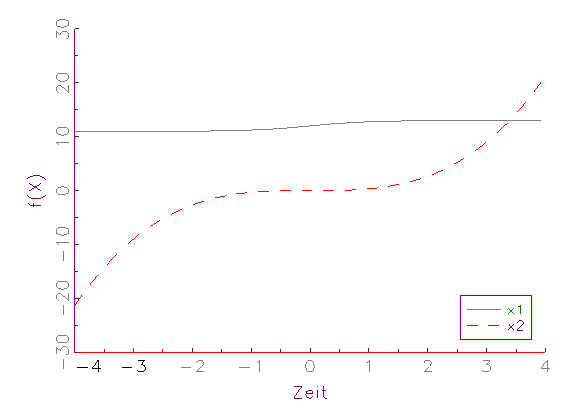
(a) Zeitreihen-Diagramm von nichtnormierten Variablen
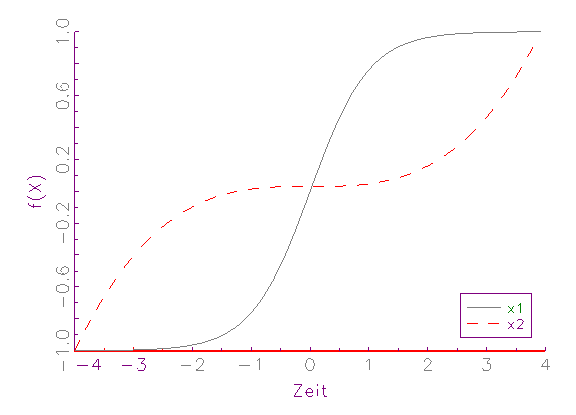
(b) Zeitreihen-Diagramm von [-1,1]-Intervall-normierten Variablen
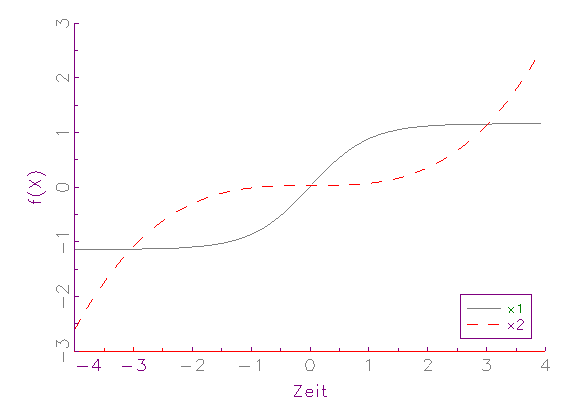
(c ) Zeitreihen-Diagramm von Mittelwert-Varianz-normierten Variablen
Abbildung 3.4: Normierung der Daten.
Vor der Normierung (vergleiche Abbildung 3.4a) besitzt die Variable x2
einen deutlich grösseren Streuungs- und Wertebereich als die Variable
x1. Bei einer nichtlinearen Schätzung (vergleiche Abschnitt 3.2.3)
würde dieser Sachverhalt aus den oben genannten Gründen dazu
führen, dass der Einfluss von x2 über x1
dominiert. Nach der [-1,1]-Intervall-Normierung (vergleiche Abbildung 3.4b)
beziehungsweise Mittelwert-Varianz-Normierung (vergleiche Abbildung 3.4c)
befinden sich die Variablen dagegen auf demselben numerischem Rang, weswegen
sie zu gleichen Teilen bei der Schätzung berücksichtigt werden.
Durch die Normierung ergeben sich weitere Vorteile, zum Beispiel im
Zusammenhang mit den später beschriebenen Gradienten- und
Diagnoseverfahren, worauf hier nicht näher eingegangen wird. Zu
erwähnen ist jedoch, dass nach einer Normierung der Trainingsmenge
immer auch eine Normierung der anderen Mengentypen zu erfolgen hat. Nur so kann
die (implizite) Annahme bestehen bleiben, dass alle Mengen der gleichen
Grundgesamtheit entstammen. Damit dem neuronalen Netzwerk dabei keine
Informationen zugeleitet werden, die es unter realen Bedingungen nicht zur
Verfügung hätte, müssen die Normierungsstatistiken der
Trainingsmenge (Mittelwerte, Varianzen, Minima und Maxima) jeweils auch die
Basis für die Normierung der restlichen Mengen bilden.
Die Festlegung der Eigenschaften des neuronalen Netzwerks stellt den zentralen
Schritt im neurometrischen Modellbildungsprozess dar. Die Suche nach der
optimalen Spezifikation zur Approximation einer wahren Funktion ist nicht
trivial, und in der Literatur der Neuroinformatik lassen sich nur wenige
Kriterien und Verfahren finden, die eine automatisierte, problembezogene
Konstruktion derselben ermöglichen. In den meisten Fällen behilft man
sich stattdessen mit Methoden von eher heuristischer Natur, die zumindest
allgemeine Anhaltspunkte zur Modellbildung beisteuern können. Wie weiter
unten beschrieben wird, bietet Neurometricus im Gegensatz dazu eine Reihe von
Strategien zur Modell-Selektion an, die auf statistischen Methoden basieren.
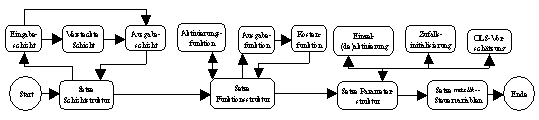
Abbildung 3.5: nn_Spec-Funktion von Neurometricus.
Mit der nn_Spec-Funktion von Neurometricus, die auf diverse, vom
Benutzer
gesetzte globale Variablen zurückgreift, lässt sich eine
beliebige
Spezifikation in Form eines vorwärtsgekoppelten, (mehrschichtigen)
neuronalen
Netzwerks implementieren. Wie Abbildung 3.5 zeigt, wird zuerst die
Schichtstruktur
aufgebaut. Während die Anzahl der Neuronen in der Eingabe- und
Ausgabeschicht durch die Anzahl der Eingabe- beziehungsweise Ausgabevariablen
determiniert ist, kann die Anzahl der versteckten Schichten und der versteckten
Neuronen frei gestaltet werden. Danach wird die Funktionsstruktur definiert:
Jede versteckte Schicht bekommt eine Aktivierungsfunktion, die Ausgabeschicht
eine Ausgabefunktion, und das Lernverfahren eine Kostenfunktion zugewiesen. Zu
diesem Zweck stehen mehrere lineare und nichtlineare Aktivierungs-
beziehungsweise Ausgabefunktionen, sowie derzeit eine Kostenfunktion zur
Verfügung. Anschliessend findet die (Zufalls-)Initialisierung der
Gewichte-/Parameterstruktur statt, wobei zwischen den folgenden drei
Parametertypen unterschieden wird:
-
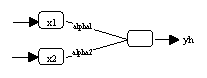
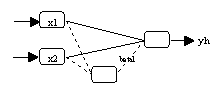
Gamma-Typ: Die Parameter dieses Typs gewichten die Signale, die von den
Eingabeneuronen beziehungsweise versteckten Neuronen zu den versteckten
Neuronen geleitet werden.
-
Beta-Typ: Die Parameter dieses Typs gewichten die Signale, die von den
versteckten Neuronen zu den Ausgabeneuronen geleitet werden.
-
Alpha-Typ: Die Parameter dieses Typs gewichten die Signale, die von den
Eingabeneuronen zu den Ausgabeneuronen geleitet werden.
Alle Parametertypen können, müssen aber nicht gleichzeitig in einem
neuronalen Netzwerk aktiv sein (vergleiche Abbildung 3.6). Ihre Werte sind
entweder fest vorgegeben oder werden zufällig aus einen Intervall gezogen,
dessen Grenzen durch den jeweiligen Parametertyp vorgegeben sind. Man kann die
Alpha-Parameter alternativ dazu auch mit denjenigen Parametern belegen, die ein
linearen Regressionsmodell aus den Eingabe- und Ausgabevariablen berechnet
(Ordinary Least Squares- beziehungsweise OLS-Vorschätzung). Alle
allokierten Parameter lassen sich durch einen Dimmfaktor zusätzlich
verstärken oder bis auf null herabsetzen, wodurch sehr individuelle
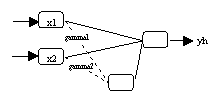
Spezifikationen kreierbar sind. Das Beispiel in Abbildung 3.6c zeigt, dass
Neurometricus auch eine Spezifikation von neuronalen Netzwerken mit mehreren
Ausgabevariablen ermöglicht.
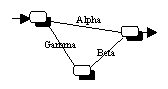
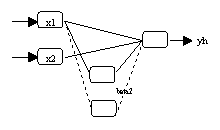
(a) Neuronales Netzwerk mit Bezeichnung der Parameter
(b) Neuronales Netzwerk mit einer
Ausgabevariable |
(c) Neuronales Netzwerk mit mehreren
Ausgabevariablen |
Abbildung 3.6: Neurometricus-Spezifikationen.
Zuletzt werden durch die nn_Spec-Funktion wichtige Steuervariablen
für das maxlik.src-Modul gesetzt, welches für die in Abschnitt
3.2.3 beschriebene Schätzung der Parameter zuständig ist. Durch die
Steuervariablen wird unter anderem festgelegt, nach welchem Gradientenverfahren
die Parameter zu optimieren sind, wie viele Schätzschritte maximal
durchgeführt werden sollen, welche Verbesserung des Kostenfunktionswerts
je Iterationsschritt erreicht werden muss usw.
Mit jeder Festlegung der Modelleigenschaften, die der Benutzer oder ein
entsprechendes
Verfahren trifft, wird das Approximationspotenzial des zugrunde liegenden
neuronalen
Netzwerks eingeschränkt. Es gilt generell, dass sich die Güte
der
Approximation durch die Allokierung von zusätzlichen Parametern beliebig
verbessern lässt. Wie in Abschnitt 2.3 im Zusammenhang mit dem
Bias-Varianz-Dilemma erläutert wurde, korreliert jedoch die Anzahl der
Parameter positiv mit der Varianz der Schätzung. Neben den in der
Statistik üblichen Gütemassen wie zum Beispiel SSE, MSE,
R2 etc., können mit Neurometricus deshalb auch sogenannte
Informations- und Selektionskriterien bestimmt werden. Hierbei handelt
es sich um spezielle Gütemasse, die bei ihrer Berechnung die
Komplexität des geschätzten Modells bestrafen, indem sie die
quadrierten Residuen zu der Anzahl der Parameter in Beziehung setzen. Die
Informationskriterien (IC), die auch bei den später erläuterten
Strategien zur statistischen Modell-Selektion von Neurometricus Verwendung
finden, sind unter anderem von Akaike (1973), Schwarz (1978) und Murata et al.
(1994) entwickelt worden.
An dieser Stelle werden zwei weitere Verfahren zur Bestimmung der optimalen
Spezifikation vorgestellt, die derzeit nicht als Funktionen in Neurometricus
implementiert sind. Durch eine geringügige Erweiterung des Lernverfahrens
können sie jedoch nachträglich realisiert werden. Bei der
Regularisierung wird die Kostenfunktion um einen Term erweitert, der die
Komplexität des neuronalen Netzwerks (d.h. die Anzahl der Parameter)
bestraft. Das Lernverfahren kann dann dahin gehend modifiziert werden, dass
es kleinen Parametern die Tendenz gibt, auf null hin abzunehmen. Zum anderen
werden Pruning-Techniken diskutiert, bei denen versucht wird, nach der
Schätzung durch Deaktivierung einzelner Parameter ihre Redundanz zu
beweisen.
Die bisher vorgestellten Strategien zur Modell-Selektion verlangen die
Festlegung der Spezifikation, mit dem die wahre Funktion approximiert werden
soll, durch den/die Benutzer. Neurometricus enthält jedoch auch
Strategien, die zu einer automatisierten, statistischen Modell-Selektion
eingesetzt werden können, wenn maximal eine versteckte Schicht mit
beliebig vielen versteckten Neuronen und eine Ausgabevariable produziert werden
soll. Die im Folgenden beschriebenen Strategien zur statistischen
Modell-Selektion basieren auf den theoretischen Arbeiten von White (1988),
Teräsvirta et al. (1993) sowie Anders/Korn (1996). Durch Neurometricus ist
erstmals die Möglichkeit gegebene, die dort gemachten theoretischen
Erkenntnisse in die Praxis umzusetzen (vergleiche Abschnitt 3.3).
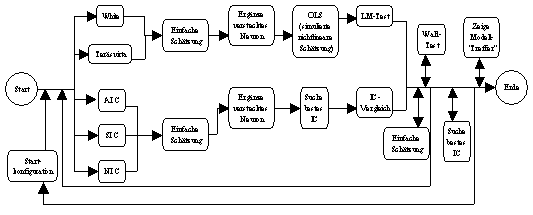
Abbildung 3.7: nn_MS-Funktion von Neurometricus.
Obwohl im Detail verschieden, sind die prinzipiellen Vorgehensweisen der White-
und der Teräsvirta-Strategie ähnlich zueinander (vergleiche Abbildung
3.7):
-
Basismodell: Der Benutzer muss ein erstes Schätzmodell
"von Hand" spezifizieren. Üblicherweise handelt es sich dabei um
ein neuronales Netzwerk, welches ausschliesslich aus Alpha-Parametern
besteht (vergleiche Abbildung 3.8a).
-
Schätzung des aktuellen Neuronalen Netzwerks: Nachdem die Parameter
des aktuellen neuronalen Netzwerks geschätzt worden sind, werden die
resultierenden Residuen und der SSE1 bestimmt.
-
Modellerweiterung: Das neuronalen Netzwerk wird um ein verstecktes
Neuron erweitert. Nur diejenigen Eingabeneuronen, die mit allen vorherigen
versteckten Neuronen verbunden sind, werden auch mit dem zusätzlichen
versteckten Neuron verbunden (vergleiche Abbildung 3.8b und Abbildung 3.8d).
-
Simulation einer nichtlineare Schätzung: Um das gesamte
nichtlineare Potenzial der originalen Eingabemenge in Form neuer Variablen zu
simulieren, wird durch die White- beziehungsweise Teräsvirta-Strategie
eine neue Eingabemenge gebildet. Es wird mit ihr eine lineare Schätzung
der Residuen aus (2) durchgeführt und dadurch der SSE2 bestimmt.
-
Hypothesen-Prüfung: Aus dem SSE1 und dem SSE2 wird eine
Prüfgrösse gebildet, die einer hypothetischen
Chi-Quadrat-Verteilung gehorcht. Es wird danach die Nullhypothese "die
Verbesserung des SSE2 gegenüber dem SSE1 rechtfertigt die
Modellerweiterung nicht" bei einem gegeben Sicherheitsniveau getestet. Bei
Ablehnung der Nullhypothese ist der neue Beta-Parameter signifikant
identifiziert, und es wird mit (6) fortgefahren, sonst bei (8) abgebrochen
(vergleiche Abbildung 3.8c). Man bezeichnet die Schritte von (3) bis (5) als
Langrange-Multiplier-Test (LM-Test). Um gültige Ausagen zu
erhalten, muss eine (asymptotische) Normalverteilung der geschätzten
Parameter angenommen werden.
-
Schätzung des erweiterten Modells: Nachdem der zusätzliche
Beta-Parameter als signifikant von Null abweichend angenommen werden kann und
damit die Notwendigkeit des versteckten Neurons gezeigt wurde, wird das
erweiterte Modell neu geschätzt.
-
Wald-Test: Die Modellerweiterung von (3) allokierte neben einem
Beta-Parameter auch ein oder mehrere Gamma-Parameter, deren Signifikanz nicht
überprüft wurde. Durch die Schätzung des erweiterten Modells in
(6) müssen zudem auch die Signifikanzen der alten Gamma-Parameter neu
überprüft werden. Der Wald-Test prüft hierzu die Nullhypothese
"der betrachtete Parameter hat einen Wert von Null" mit einer
chi-quadrat-verteilten Prüfgrösse. Wird der Wald-Test so
häufig angenommen, dass ein verstecktes Neuron eingespart werden
kann, wird mit (8) abgebrochen, sonst mit (2) fortgefahren (vergleiche
Abbildung 3.8d).
-
Abbruch: Es ist ein Modell spezifiziert worden, bei dem alle Parameter
als signifikant abweichend von Null angenommen werden dürfen und dessen
MSE sich alleine aus einem Störterm zusammensetzt.
(a) Lineares Basismodell
(b) Ergänzung eines versteckten Neurons
(c) Prüfung der Signifikanz der Gamma-Parameter
(d) Resultierendes erweitertes Modell
Abbildung 3.8: Statistische Modell-Selektion bei der White-
beziehungsweise Teräsvirta-Strategie.
In Abbildung 3.8 wird an einem Beispiel die statistische Modell-Selektion durch
Anwendung der White- beziehungsweise der Teräsvirta-Strategie
demonstriert. Das Basismodell besteht zunächst ausschliesslich aus
Alpha-Neuronen (vergleiche Abbildung 3.8a). Es wird ein verstecktes Neuron
ergänzt, und die Signifikanz des beta1-Parameters durch einen
LM-Test geprüft (vergleiche Abbildung 3.8b). Durch Anwendung des
Wald-Tests wird anschliessend festgestellt, dass im Beispiel der
gamma1-Parameter signifikant von Null abweicht, nicht aber der
gamma2-Parameter (vergleiche Abbildung 3.8c). Die Strategie wird mit dem
jeweils resultierenden erweiterten Modell (vergleiche Abbildung 3.8d) so lange
wiederholt, bis die Ergänzung versteckter Neuronen keine Verbesserungen
des Approximationsfehlers mehr erbringt.
Der "Trick" hinter der White- und der Teräsvirta-Strategie
besteht darin, dass zwischen betrachteten Variablen nicht einfach ein
nichtlinearer Zusammenhang vermutet wird, da dies dazu führen könnte,
dass das zugrunde liegende Modell überparametrisiert wird. Stattdessen
wird schon vorab geprüft, ob die Nullhypothese "der wahre
Zusammenhang zwischen den Variablen ist linear" abgelehnt wird. Dadurch
können unnötige und zeitraubende Schätzungen der Parameter des
neuronalen Netzwerks verhindert werden. Darüber hinaus wird durch den
LM-Test sichergestellt, dass nur Verbesserungen bezüglich des
Approximationsfehlers (und nicht des Störterms) zur Erweiterung des
neuronalen Netzwerks führen. Im Zusammenhang mit der
Teräsvirta-Strategie ist zu erwähnen, dass die den versteckten
Neuronen zugeordnete Aktivierungsfunktion hinsichtlich ihrer Eignung für
den LM-Test zu untersuchen ist.
Strategien zur statistischen Modell-Selektion können auch durch die in
Abschnitt 3.2.2.1 erläuterten IC realisiert werden. Möglichkeiten
hierzu
stellen Anders/Korn (1996) vor: Ähnlich wie bei der White- und der
Teräsvirta-Strategie werden ausgehend von einem Basismodell sukzessive
versteckte Neuronen zu einem neuronalen Netzwerk hinzugeschaltet. Die
Signifikanz
der Parameter wird jedoch nicht mit einem LM-Test überprüft.
Stattdessen wird für das Ausgangsmodell zunächst ein
ausgewähltes IC berechnet. Anschliessend wird getestet, ob sich durch
Aktivierung beziehungsweise Deaktivierung der Parameter, die in Verbindung mit
dem neuen versteckten Neuron stehen, eine Verbesserung des IC erreichen
lässt. Ein zusätzlicher Parameter wird nur dann in das Modell
aufgenommen, wenn dadurch das IC einen geringeren Wert annimmt. Die IC, die
Neurometricus für die IC-Strategien zur statistischen Modell-Selektion
anbietet, sind das Akaike (1973) Informationskriterium (AIC), das Schwarz
(1978) Informationskriterium (SIC) und das Netzwerk-Informationskriterium (NIC)
von Murata et al. (1994).
Wie in Abschnitt 3.2.2 beschrieben, bekommen die Parameter des Modells bei der
Spezifikation üblicherweise Zufallswerte zugewiesen, die aus einem
Intervall um Null gezogen werden. Um die wahre Funktion zu approximieren,
müssen die Parameter geschätzt werden. In diesem Abschnitt werden die
in Neurometricus integrierten Methoden beschrieben, durch die sich
(annähernd) optimale Parameter bestimmen lassen.
Durch die Kostenfunktion von Neurometricus wird der MSE (vergleiche Abschnitt
2.3) in Abhängigkeit von den n Parametern des zugrunde liegenden
neuronalen Netzwerks berechnet. Werden im Rahmen der grafischen
Kostenfunktionsanalyse n-2 Parameter auf einem konstantem Niveau
gehalten und die restlichen zwei Parameter diskret innerhalb eines vorher
angegebenen Intervalls variiert, so kann das abstrakt gegebene,
(n+1)-dimensionale Fehlergebirge der MSE-Kostenfunktion in
dreidimensionale Unterräume aufgespalten und in grafischer Weise
dargestellt werden (vergleiche Abbildung 3.9).
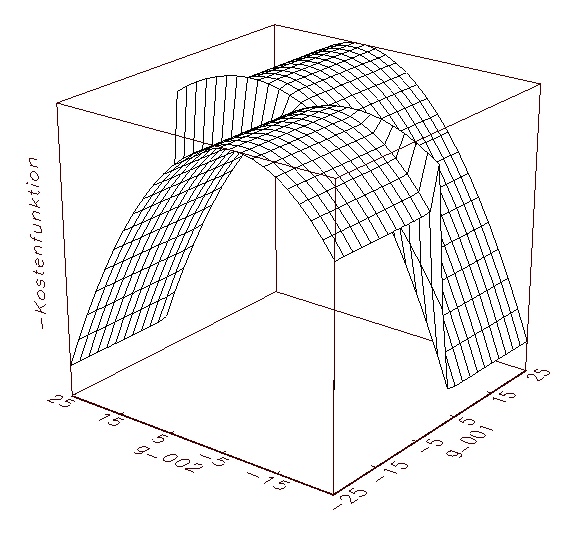
(a) Kostenfunktionsanalyse-Schaubild mit negiertem MSE-Gebirge
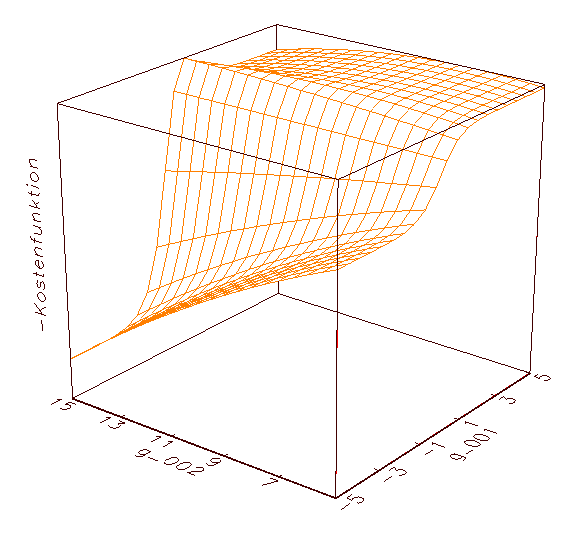
(b) Erste Annäherung an eines der beiden globalen Maxima von (a)
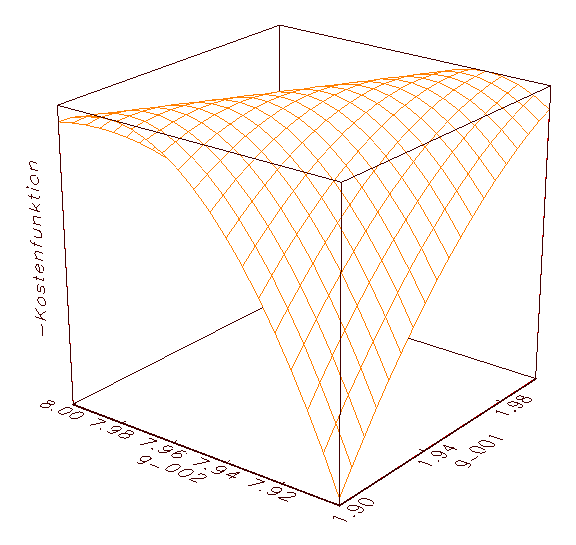
(c) Zweite Annäherung an eines der beiden globalen Maxima von (a)
Abbildung 3.9: Grafische Kostenfunktionsanalyse. Aus optischen
Gründen wurde das MSE-Gebirge negiert dargestellt.
Auf diese Weise lässt sich der Einfluss einzelner Parameter auf
die Kostenfunktion des zugrunde liegenden Modells analysieren. Anhand obiger
Abbildung 3.9 wird deutlich, dass die optimalen Parameter jeweils die
höchste Erhebung im Fehlergebirge der negierten MSE-Kostenfunktion
kennzeichnen (in diesem Fall ergeben sich für die Parameter g_001
und g_002 die optimalen Werte 1.95 und 7.95; vergleiche 3.8c). Die
Ergebnisse der grafischen Kostenfunktionsanalyse können zum Beispiel
verwendet werden, um die Zufallsinitialisierung der Parameter für die im
folgenden beschriebenen numerischen Schätzverfahren effektiver zu
gestalten.
Zur automatisierten Bestimmung der (annähernd) optimalen Parameter eines
Modells
wird in Neurometricus die sogenannte Maximum-Likelihood-Methoden eingesetzt
(vergleiche Abschnitt 2.2). Dabei handelt es sich um ein Verfahren zur
Gewinnung von Punktschätzungen für die Parameter einer
Grundgesamtheit. Die Schätzer sind unter ziemlich allgemeinen Bedingungen
konsistent und asymptotisch normalverteilt, jedoch nicht immer erwartungstreu.
Unter den Annahmen, dass die Störterme der gesuchten, wahren Funktion
multivariat normalverteilt sind und eine konstante Kovarianz, sowie einen
Erwartungswert von Null besitzen, kann die Maximum-Likelihood-Methode
mathematisch in die Methode der kleinsten Quadrate (vergleiche Abschnitt 2.3)
überführt werden. Die letztgenannte Methode basiert auf der
Minimierung des MSE, der - wie oben beschrieben - mithilfe der Kostenfunktion
berechnet werden kann. Durch die Maximierung der negierten Kostenfunktion
werden daher Schätzer für die Parameter der wahren Funktion bestimmt.
Die Extrema der Kostenfunktion können nur in wenigen Fällen
analytisch bestimmt werden. Zum überwiegenden Teil muss die
Maximierung daher iterativ auf numerischem Weg erfolgen, zum Beispiel durch die
sogenannten Gradientenverfahren. Im folgenden sind die wesentlichen vier
Schritte beschrieben, in die sich diese Verfahren gliedern lassen.
-
Wahl der Startwerte für die Parameter: Die Parameter werden in der
Regel mit einem Zufallswert belegt, der möglichst in der Nähe ihres
optimalen Wertes liegen sollte. Zur Zufallsinitialisierung der Parameter kann -
wie oben ausgeführt - die grafische Kostenfunktionsanalyse eingesetzt
werden.
-
Bestimmung der Abstiegs-/Aufstiegsrichtung: Um den MSE zu verkleinern
beziehungsweise um die negierte Kostenfunktion zu vergrössern,
müssen die Parameter entweder vergrössert oder verkleinert
werden. Diese Änderung wird in jedem Iterationsschritt durch eine
Richtungsmatrix festgelegt (vergleiche Abbildung 3.10d).
-
Bestimmung der Schrittlänge: Der Vektor der Schrittlängen gibt
an, wie stark sich die einzelnen Parameter in der berechneten Richtung
ändern sollen, um die grösste Minimierung des MSE zu erreichen.
-
Überprüfung der Abbruchkriterien: Numerische Verfahren
konvergieren unter bestimmten Umständen nur asymptotisch oder
überhaupt nicht. Um in jedem Fall einen Abbruch des numerischen
Iterationsprozesses zu erzwingen, müssen bestimmte Abbruchkriterien
gesetzt und überprüft werden, zum Beispiel eine maximale Anzahl von
Iterationsschritten, eine minimale Änderung des MSE je Iterationsschritt
usw. Wurde eines dieser Kriterien erfüllt, bricht das
Gradientenverfahren ab, sonst wird mit Schritt 2 fortgefahren.
Um die Vorgehensweise der Gradientenverfahren zu verdeutlichen, ist in
Abbildung 3.10 eine univariate negierte Kostenfunktion mit ihrer ersten und
zweiten Ableitungen sowie ihrer Richtungsfunktion gegeben. Durch Bestimmung der
Nullstellen der ersten Ableitung werden die Extrema gefunden (vergleiche
Abbildung 3.10b). Ist die zweite Ableitung an dieser Stelle kleiner als Null,
so liegt ein Maximum vor (vergleiche Abbildung 3.10c). Im multivariaten Fall
wird in dazu analoger Weise der Gradienten und die Hessematrix betrachtet.
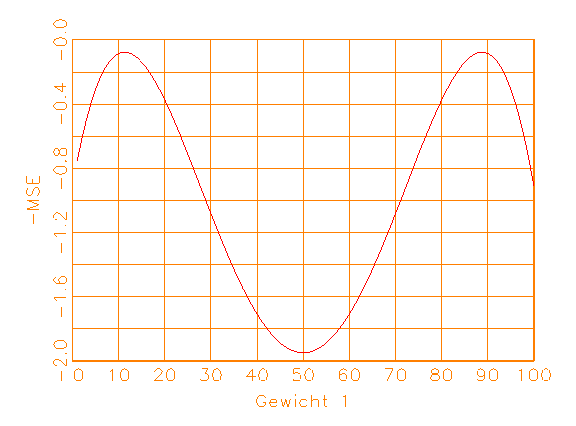
(a) Negierte MSE-Kostenfunktion |
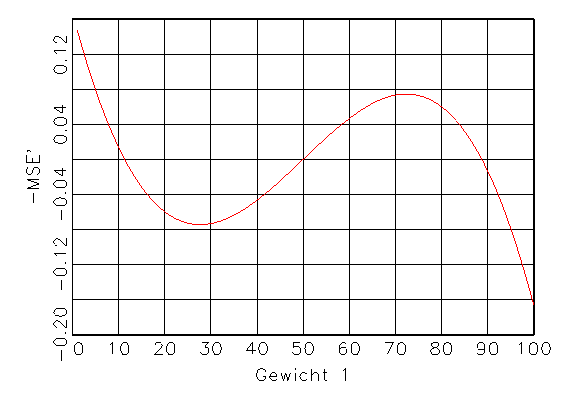
(b) Erste Ableitung von (a) |
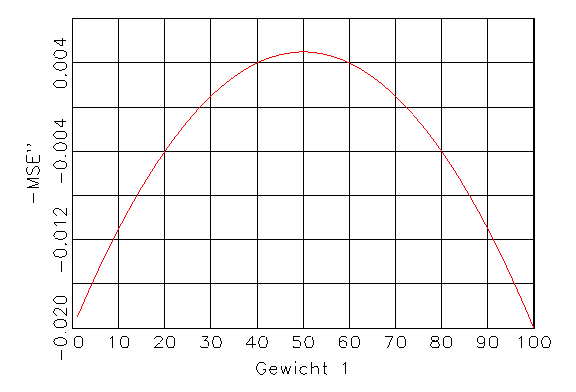
(c) Zweite Ableitung von (a) |
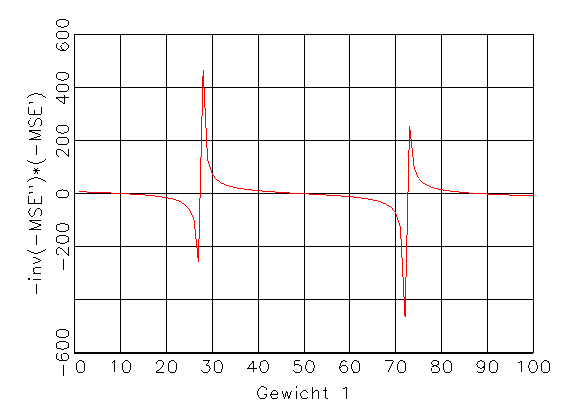
(d) Richtungsfunktion, die sich durch
(b) und (c) ergibt |
Abbildung 3.10: Funktionen für das Gradientenverfahren.
In Neurometricus stehen mehrere Gradientenverfahren zur Verfügung. Sie
sind in den nnestim.src- und maxlik.src-Modulen definiert worden
(vergleiche Abbildung 3.11).
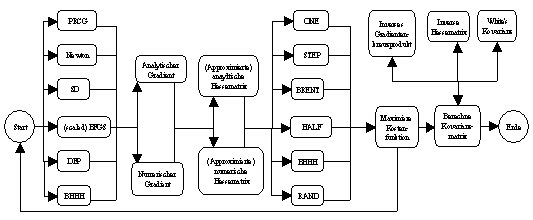
Abbildung 3.11: maxlik-Funktion von Neurometricus.
Als das fundamentalste der Gradientenverfahren präsentiert sich das
Newton-Verfahren. Hier wird in jedem Iterationsschritt die Hessematrix an der
Stelle der aktuellen Parameter neu bestimmt, und dieselbe dann zur Berechnung
der Richtungsmatrix benutzt. In Anhang D wird das Taylor-Verfahren beispielhaft
durchgeführt.
Die sogenannten Verfahren zweiter Ordnung, zu denen das BFGS- (Broyden,
Fletcher, Goldfarb und Shannon) und das DFP-Verfahren (Davidon, Fletcher
und Powell) gehören, berechnen die Hessematrix nur im ersten
Iterationsschritt und approximieren sie danach. Sie benötigen in der Regel
mehr Iterationsschritte als das Newton-Verfahren. Durch den verringerten
Rechenaufwand der approximativen Hessematrix-Bestimmung finden sie das Minimum
der Kostenfunktion jedoch im Allgemeinen schneller. Mit einem Substitut der
Hessematrix wird dagegen beim BHHH-Verfahren (Berndt, Hall, Hall und
Hausman) gearbeitet. Die Richtungsmatrix berechnet sich hier aus dem Gradienten
und dem sogenannten Gradientenkreuzprodukt, was bei relativ kleinen
Eingabemengen weitere Geschwindigkeitsvorteile mit sich bringt.
Die Verfahren erster Ordnung, bestehend aus dem SD- (Steepest
Descent) und PRCG-Verfahren (Polak-Ribiere-type Conjugate Gradient),
verzichten bei der Berechnung der Richtungsmatrix auf die Hessematrix
beziehungsweise einem Substitut von ihr, wodurch sie vergleichsweise wenig
Speicher- und Rechenressourcen beanspruchen. Bei ungünstig gewählten
Startwerten der Parameter eignen sie sich damit besonders zu einer ersten,
schnellen Annäherung an ein Maximum. In der Region um das Maximum herum
konvergieren sie jedoch schlecht.
Um das Kovergenzverhalten den jeweiligen Umständen anpassen zu
können, hat der Anwender die Möglichkeit, während des
numerischen Iterationsprozesses zwischen den gezeigten Gradientenverfahren
interaktiv zu wechseln. Die für die Berechnung der Richtungsmatrix
benötigte Invertierung der Hessematrix beziehungsweise ihres Ersatzes
erfolgt im Übrigen durch die besonders schnelle und numerisch stabile
Methode der Cholesky-Dekomposition.
Während des numerischen Iterationsprozesses kann der Gradient und die
Hessematrix der Kostenfunktion wahlweise auf numerischem oder analytischem Weg
bestimmt werden (vergleiche Abbildung 3.11). Die numerische Vorgehensweise hat
den Vorteil, dass sie auf beliebige (Schätz-)Funktionen angewendet
werden kann, und den Nachteil, dass sie rechenintensiv und damit langsam
ist. Im Vergleich dazu erfolgt die analytische Berechnung im Schnitt schneller.
Wie die analytischen ersten und zweiten partiellen Ableitungen der
Kostenfunktion für beliebige Spezifikationen innerhalb von Neurometricus
funktional gebildet wurden, ist in Anhang C beschrieben.
Bei allen Gradientenverfahren besteht die Gefahr, dass der Abstiegsweg
(beziehungsweise Aufstiegsweg) im Zickzack verläuft, und dadurch nie ein
Extrema erreicht wird. Um ein solches Fehlverhalten zu verhindern, stehen in
Neurometricus eine Reihe von Schrittlängen-Berechnungsverfahren zur
Verfügung, die sich wie folgt beschreiben lassen:
Das One-Verfahren setzt die Schrittlänge auf eine konstante
Grösse von Eins, wodurch das oben beschriebene Problem jedoch nicht
verhindert wird. Alle anderen Verfahren variieren daher die Schrittlänge
in Abhängigkeit von dem sich ergebenden Kostenfunktionswert. Ohne hier
näher auf die Unterschiede der Stepbt-, Brent-, Half- und
BHHHStep-Verfahren einzugehen, kann durch sie in jedem Fall
sichergestellt werden, dass die Parameter in der zuvor berechneten
Richtung nur so stark modifiziert werden, dass der Kostenfunktionswert in
jedem Iterationsschritt kleiner wird. Lässt sich auf diese Weise kein
kleinerer Kostenfunktionswert mehr finden, wird - automatisch oder interaktiv -
durch das Random Search-Verfahren innerhalb eines bestimmten
Zufallsradius nach einer alternativen Schrittlänge gesucht. Versagt auch
dieser Versuch, bricht das Gradientenverfahren ab.
Gradientenverfahren sind lokale Optimierungsalgorithmen, da sie das
globale Minimum einer (Schätz-)Funktion nicht generell finden können.
Der Grund für dieses Verhalten sei durch die in Abbildung 3.12 gegebenen
Grafik einer bivariaten Kostenfunktion veranschaulicht: Man kann sich den von
den Gradientenverfahren im Laufe des numerischen Iterationsprozesses
veränderten Parameterpunkt nämlich als einen Ball vorstellen, der
zufällig über dem Fehlergebirge fallen gelassen wird, in das
nächstgelegen Tal rollt und dort liegen bleibt, unabhängig davon, ob
es sich dabei um die tiefste Stelle handelt oder nicht.
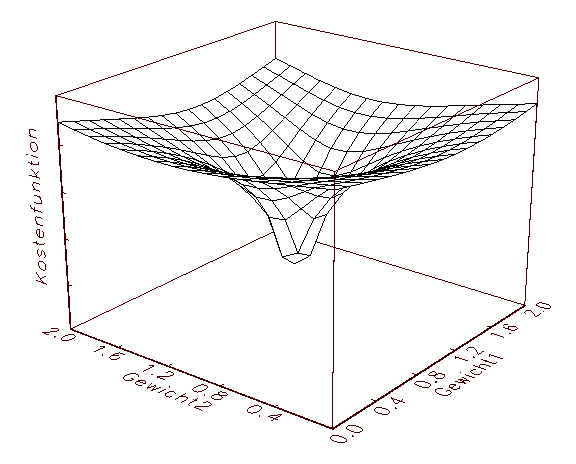
(a) Bivariate Kostenfunktion mit einem globalen Minimum
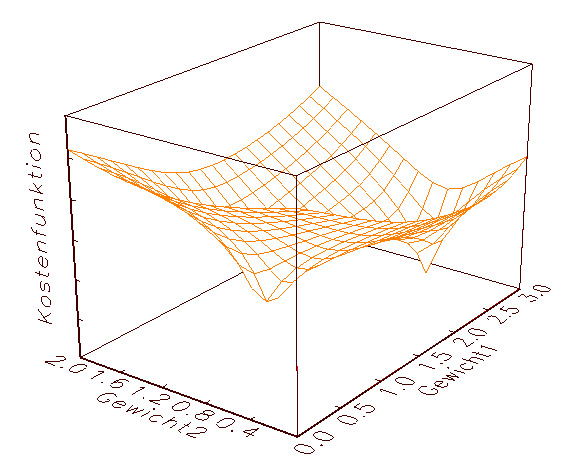
(b) Bivariate Kostenfunktion mit einem lokalen und einem globalen Minimum

(c) Bivariate Kostenfunktion mit einer grossen Anzahl von Minima
Abbildung 3.12: Fehlergebirge von bivariaten Kostenfunktionen.
In der Literatur werden verschiedentlich auch globale Optimierungsalgorithmen
diskutiert, mit denen auch bei schlecht gewählter Zufallsinitialisierung
der Parameter die globalen Extrema der Kostenfunktion bestimmt werden
können. Beispiele hierfür sind die genetischen Algorithmen, das
"simulierte Ausglühen" und der Sintflut-Algorithmus. Für
die vorliegende Arbeit sind sie jedoch nicht weiter von Interesse, denn der mit
ihnen verbundene Aufwand steht offenbar in keinem Verhältnis zu dem
Ertrag, den sie erbringen.
Um den zu erwartenden Approximationsfehler eines neuronalen Netzwerks
bezüglich unbekannter Daten zu prognostizieren, wurden in Neurometricus
das Bootstrap-, Jackknife- und Cross Validation-Verfahren
integriert. Bei jedem dieser Resampling-Verfahren wird die einfache
Schätzung n-mal hintereinander durchgeführt, wobei jeweils
individuelle Stichproben betrachtet werden (vergleiche Abbildung 3.13).
Interessant sind Resampling-Verfahren vor allem im Zusammenhang mit der
Analyse von Variablen mit grossen Störtermen (wie zum Beispiel
Finanzmarktdaten).
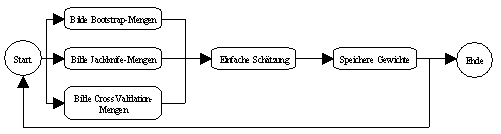
Abbildung 3.13: Resampling-Verfahren von Neurometricus.
Eine Bootstrap-Menge wird durch zufälliges
Ziehen-mit-Zurücklegen aus der ursprünglichen Stichprobe generiert.
Dadurch besitzt jede Bootstrap-Menge zwar den gleichen Umfang, aber
andere Beobachtungen als das Original. Mithilfe der n
Bootstrap-Mengen und der n Schätzungen können dann
interessierende Statistiken berechnet und hinsichtlich ihrer Verteilung
analysiert werden. Das Bootstrap-Verfahren ermöglicht es, die
Varianzen einzelner Parameter auch dann korrekt zu bestimmen, wenn das
zugrunde liegende Modell fehlspezifiziert wurde.
Zur Bildung der n Jackknife-Menge werden vor jeder Schätzung
v Beobachtungen aus der ursprünglichen Stichprobe entnommen. Dabei
ist n beziehungsweise v so gewählt, dass dem neuronalen
Netzwerk alle verfügbaren Beobachtungen mindestens einmal zur
Schätzung präsentiert werden. Danach können interessierende
Statistiken in gleicher Weise wie beim Bootstrap-Verfahren analysiert
werden. Gegenüber dem Bootstrap-Verfahren besitzt das
Jackknife-Verfahren den Vorteil, dass durch die deterministische
Mengenbildung weniger Zufall in die Schätzungen eingeht. Jedoch sind die
Schätzungen dafür in der Regel mit grösseren
Standardabweichungen behaftet.
Auch die Cross-Validation-Mengen werden durch Teilung der
ursprünglichen Stichprobe in n disjunkte Mengen gebildet. Im
Gegensatz zum Jackknife-Verfahren werden interessierende Statistiken
jedoch mit den v Beobachtungen der jeweiligen Restmengen
(Validierungsmengen) berechnet. Auf diese Weise kann zum Beispiel über den
Mittelwert des MSE der zu erwartende Approximationsfehler einer Vorhersage des
zugrunde liegenden Modells berechnet werden.
Zufall wirkt sich in zweierlei Hinsicht auf die Modellbildung aus: Durch die
stochastische Datenteilung beziehungsweise Datenbildung und durch die
Zufallsinitialisierung der Parameter. Es gilt im Allgemeinen, dass zum
Beispiel bei Anwendung des Bootstrap-Verfahrens die Varianz einer
Schätzung stärker durch die dort gegebenen stochastischen
Mengenbildung beeinflusst wird als durch die Zufallsinitialisierung der
Parameter. Das setzt aber eine spezielle Behandlung der Parameter voraus, wie
im Folgenden anhand eines Beispiels demonstriert wird.
In Neurometricus gibt es eine globale Variable, durch die sich festlegen
lässt, ob vor jeder Resampling-Schätzung eine neue
Zufallsinitialisierung der Parameter vorgenommen wird oder ob die jeweils
letzten Parameter beibehalten werden. Wie in den Abbildungen 3.14 und 3.15
anhand der grafischen Parameteranalyse von Neurometricus veranschaulicht wird,
streuen die Parameter des in Abbildung 3.16 gezeigten Modells nach 50
Bootstrap-Schätzungen im ersten Fall (vergleiche Abbildung 3.14)
erheblich stärker als nach Deaktivierung der Zufallsinitialisierung der
Parameter (vergleiche Abbildung 3.15).
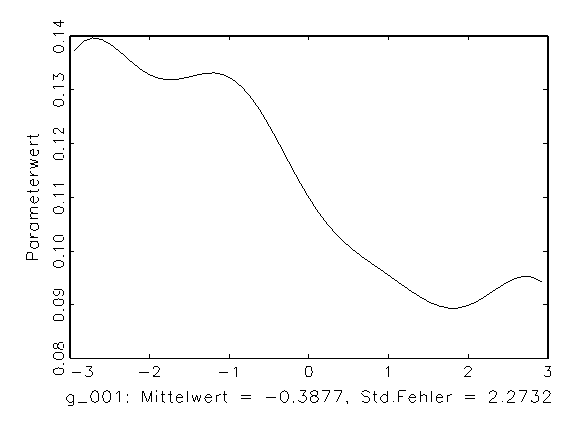
(a) Histogramm von Parameter g_001 |
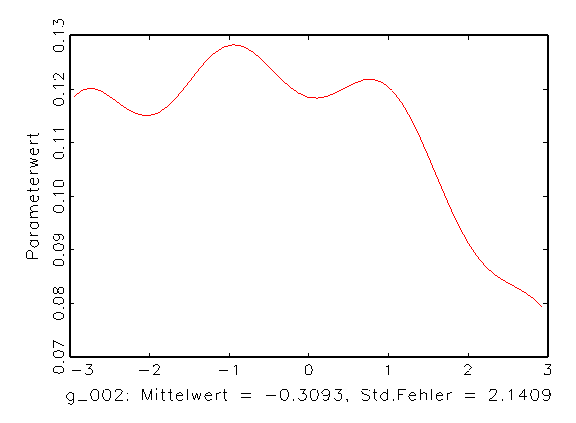
(b) Histogramm von Parameter g_002 |
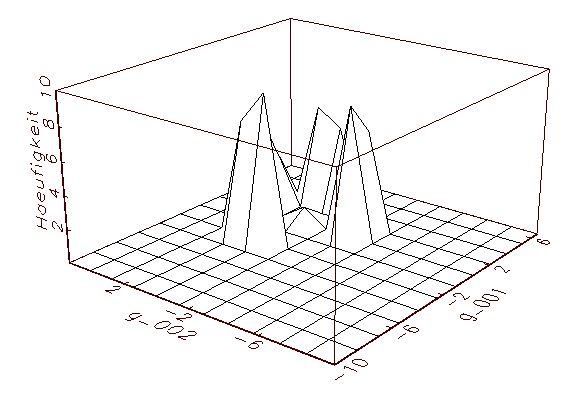
(c) Parameteranalyse-Schaubild mit gemeinsamer
Häufigkeit der Parameter g_001 und ag002
Abbildung 3.14: Grafische Parameteranalyse nach einer
Bootstrap-Schätzung mit aktivierter Zufallsinitialisierung
der Parameter.

(a) Dichte von Parameter g_001 |

(b) Dichte von Parameter g_002 |
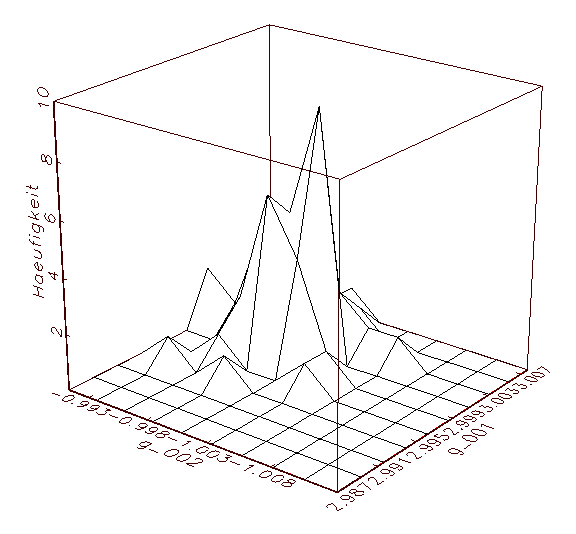
(c) Parameteranalyse-Schaubild mit gemeinsamer
Häufigkeit der Parameter g_001 und ag002
Abbildung 3.15: Grafische Parameteranalyse nach einer
Bootstrap-Schätzung mit deaktivierter
Zufallsinitialisierung der Parameter.
Der Grund für die allgemein gegebene stärkere Streuung der Parameter bei
aktivierter Zufallsinitialisierung lässt sich grösstenteils auf
Symmetrien zurückführen, die durch den Aufbau der neuronalen Netzwerke, die
quadratische Natur der MSE-Kostenfunktion und den mathematischen Eigenschaften einiger
Aktivierungsfunktionen begründet sind. Wie in Abbildung 3.16 gezeigt wird,
können nämlich die Parameter unter Umständen die Positionen und das
Vorzeichen wechseln, ohne dass sich dadurch die von einem neuronalen Netzwerk
zurückgelieferte Ausgabemenge ändert. Durch alleiniges Deaktivierung der
Zufallsinitialisierung der Parameter während der Resampling-Verfahren
werden Permutationen der Parameter jedoch nicht völlig verhindert. Einen
effektiveren Weg schlagen Rüger/Ossen (1995) vor: Sie empfehlen, die
Parameter des Modells nach jeder Schätzung in einer bestimmten Weise zu
sortieren und bezüglich ihrer Vorzeichen zu behandeln.. Zunächst
werden hierzu alle negativen Beta-Parameter positiv gemacht und die Vorzeichen
der zugehörigen Gamma-Neuronen invertiert. Anschliessend werden die
Beta-Neuronen der Grösse nach sortiert und im neuronalen Netzwerk
replatziert, wobei auch die zugehörigen Gamma-Neuronen ihre Position im
neuronalen Netzwerk ändern müssen. In Abbildung 3.16a sieht man
beispielsweise ein geschätztes Modell, welches durch den
Sortieralgorithmus von Rüger/Ossen (1995) in die einheitliche Form von
Abbildung 3.16 gebracht wird. Beide Modelle liefern eine identische
Ausgabemenge zurück.
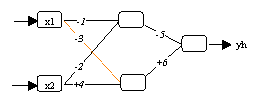
(a) Neuronales Netzwerk mit geschätzten Parametern
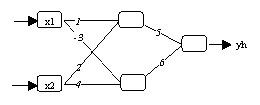
(b) Wie (a), aber nach der Sortierung der Parameter
Abbildung 3.16: Probleme mit Symmetrien.
Ein weiteres Problem bei den Resampling-Verfahren ergibt sich dadurch,
dass
der Verlauf der Kostenfunktion nicht nur von den Parametern des
zugrunde liegenden
Modells abhängt, sondern auch von der Menge der Beobachtungen der
Variablen, die
dem neuronalen Netzwerk zur Schätzung jeweils zur Verfügung stehen.
Die
lokal optimalen Parameter des Modells nach der i-ten
Resampling-Schätzung müssen nicht mit den lokal optimalen
Parametern
der (i+1)-ten Resampling-Schätzung übereinstimmen. Man
muss daher die variierenden Parameter jeweils einem lokalen Optimum
zuordnen, um
daraus das globale Optimum des gegebenen neuronalen Netzwerks identifizieren zu
können. Rüger/Ossen (1995) verwenden hierzu ein Verfahren der
partitionierenden Cluster-Analyse, durch das sich die von den
Resampling-Verfahren ermittelten "guten" Parameter von den
"schlechten" Parametern trennen lassen. Auf diese Weise lassen sich
Modelle mit kleinerer Varianz bilden.
Die n Schätzungen der Resampling-Verfahren können zur
Bildung von speziellen Vertrauensintervalle herangezogen werden. Kennt man
beispielsweise die zukünftigen Beobachtungen der unabhängigen
Variablen X, dann können die Beobachtungen der abhängigen
Variable Y durch diese Vertrauensintervalle mit bestimmter Genauigkeit
prognostiziert werden. Abbildung 3.17 zeigt dies anhand eines schematischen
Beispiels: Die senkrecht eingezeichneten Verteilungen von Y ergeben sich
durch jeweils n Berechnungen von Y für einen bestimmten
Zeitpunkt in der Zukunft; die durchgezogene Linie verläuft durch die
zugehörigen Erwartungswerte von Y.
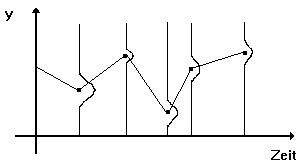
Abbildung 3.17: Resampling-Vertrauensintervalle einer Prognose.
Quelle: Angelehnt an Weigend/LeBaron (1995), S. 8.
In den vorherigen drei Schritten der Modellbildung wurden die Daten
identifiziert, das Modell spezifiziert und die Parameter des jeweils
zugrunde liegenden neuronalen Netzwerks geschätzt. Eine eingehende Diagnose
der Schätzung, der Parameter, der Residuen und der verwendeten Variablen
bilden den Abschluss jeden Durchgangs dieses Prozesses. Auf Basis vor
allem dieser Untersuchung ist ein relativ objektiver Vergleich zwischen
mehreren zur Auswahl stehenden Modellen gegeben.
Alle Funktionen von Neurometricus, die sich zur Diagnose der Ergebnisse des
geschätzten Modells einsetzen lassen, greifen auf globale Variablen
zurück, deren Inhalte durch die nn_CalcGlobals-Funktion gesetzt
werden. Hierdurch werden die folgenden Voraussetzungen geschaffen:
-
Typ der zugrunde liegenden Menge: Geschätzt wird das Modell in der
Regel ausschliesslich mit der Trainingsmenge. Die mit diesem Mengentyp
diagnostizierten Ergebnisse sagen jedoch nichts über die Fähigkeit
des Modells aus, auch mit anderen Beobachtungen der Variablen sinnvolle
Ergebnisse produzieren zu können. Zu diesem Zweck kann der Mengentyp, auf
den sich die Diagnose bezieht, gewechselt werden.
-
Analytische oder numerische Ergebnisse: Durch Aktivierung
beziehungsweise Deaktivierung der globalen Variable nn_anaok werden alle
Ergebnisse der Diagnose entweder auf Basis analytischer oder numerischer
Funktionen berechnet. Dies dient in erster Linie der Kontrolle der Korrektheit
der analytischen Funktionen. Zum Teil muss jedoch auf die numerische
Variante zurückgegriffen werden, da entsprechende analytische Funktionen
(noch) nicht implementiert worden sind.
-
Einfache oder mehrfache Schätzungen: Jede neue Schätzungen
bildet eine Matrix aus alternativen Parametern. Der Inhalt der globalen
Variable nn_basenr legt fest, ob eine Schätzung oder alle
vorhandenen Schätzungen bei der Diagnose betrachtet werden sollen. Dabei
gilt, dass auf Basis der einfachen Schätzungen je Statistik nur ein
Ergebnis berechnet wird, während es bei n Schätzungen auch
n Statistiken sind. In Abschnitts 3.2.4.6 wird darauf näher
eingegangen.
-
Typ der Kovarianzmatrix der Parameter: Viele Diagnoseergebnisse, zum
Beispiel die Varianz und die Korrelationsmatrix der Parameter, basieren auf der
Kovarianzmatrix der Parameter. Sie kann durch Setzung der globalen Variable
nn_covnr auf drei Arten geschätzt werden. Erwähnenswert ist
vor allem, dass es nach einem von White (1980) entwickelten Verfahren
möglich ist, eine heteroskedastie-konsistente Kovarianzmatrix der
Parameter zu berechnen, die eine konsistente Schätzung der Kovarianzmatrix
der Parameter erlaubt, auch wenn die a priori getroffene Annahme der
varianzkonstanten Residuen einer Überprüfung nicht standhält.
Neurometricus bietet grundsätzlich zwei Möglichkeiten, um das
gebildeten Modell hinsichtlich seiner Fähigkeit zur Approximation eines
gesuchten Zusammenhangs zwischen unabhängigen und abhängigen
Variablen zu diagnostizieren. Zum einen werden Masszahlen berechnet, die
den Fehler des Modells gegen die Anzahl seiner Parameter abwägt. Neben den
Informations- und Selektionskriterien gibt es auch Statistiken, die den Fehler
im Erwartungswert von Prognosen quantifizieren
(Prognosequalitätsmasse), denn die Güte jedes
ökonometrischen Modells muss sich daran messen, wie gut es
zukünftige Entwicklungen vorhersagen kann. Zum anderen können
Grafiken ausgegeben werden, die eine anschauliche Interpretation der Ergebnisse
des neurometrischen Modellbildungsprozesses gestatten, wie der Vergleich der
zwei Modelle in den Abbildungen 3.18 und 3.19 verdeutlichen mag.
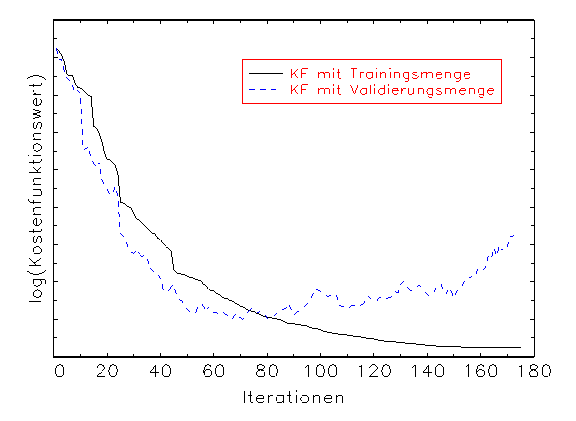
(a) Kostenfunktionswertanalyse-Diagramm
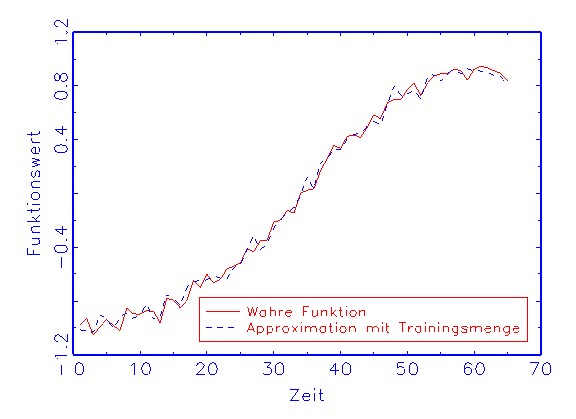
(b) Regressions-Diagramm für die Trainingsmenge
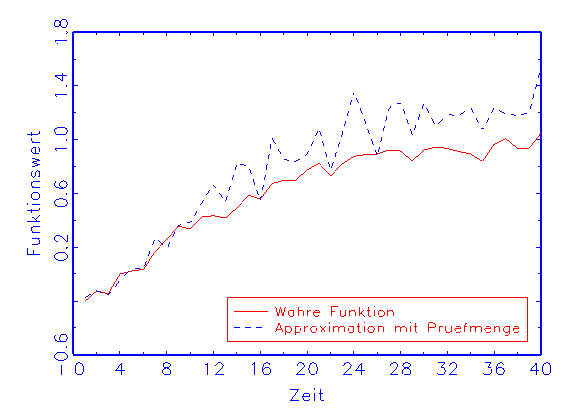
(c) Regressions-Diagramm für die Prüfmenge
Abbildung 3.18: Grafische Diagnose der Schätzung eines
überparametrisierten Modells.
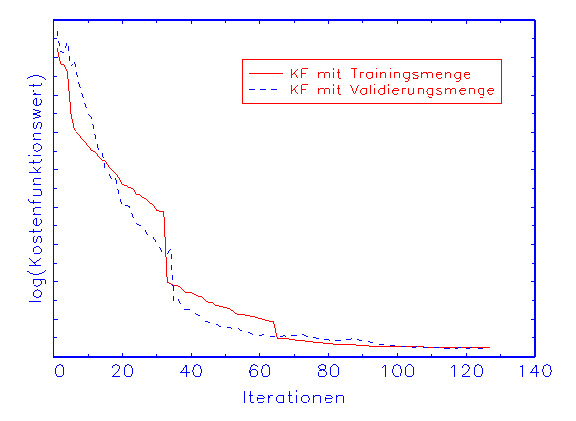
(a) Kostenfunktionswertanalyse-Diagramm
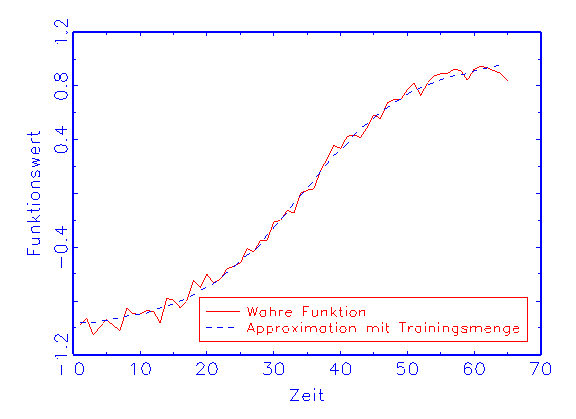
(b) Regressions-Diagramm für die Trainingsmenge
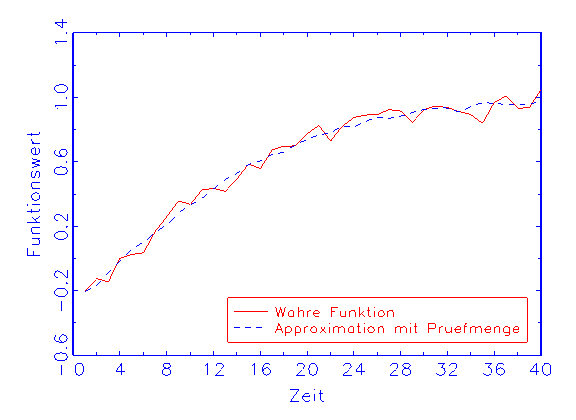
(c) Regressions-Diagramm für die Prüfmenge
Abbildung 3.19: Grafische Diagnose der Schätzung eines
korrekt spezifizierten Modells.
Eine mögliche Interpretation der oben gezeigten Ergebnisse ist, dass
das erste Modell überparametrisiert wurde, weswegen seine Benutzung zu
einer Approximation des Störterms der wahren Funktion geführt hat.
Dies macht sich durch Steigerung des Kostenfunktionswerts während der
Schätzung mit der Validierungsmenge bemerkbar, was durch eine grafische
Kostenfunktionswertanalyse angezeigt wird (vergleiche Abbildung 3.18a). Obwohl
in diesem Fall die Approximation mit der Trainingsmenge biasfrei ist
(vergleiche Abbildung 3.18b), trifft die Prüfmenge die wahre Funktion
nicht (vergleiche Abbildung 3.18c). Beim zweiten Modell dagegen nähern
sich die Kostenfunktionswerte von Trainings- und Validierungsmenge während
der Schätzung einander an (vergleiche Abbildung 3.19a). In diesem Fall
wird die wahre Funktion mit der Trainings- und der Prüfmenge ohne Bias
approximiert (vergleiche Abbildung 3.19b/c).
Wie Davidson/MacKinnon (1993), Fahrmeir/Schell (1975) und Greene (1993)
ausführen, lassen sich die Diagnoseverfahren für die Parameter
linearer
Regressionsmodelle auch auf nichtlineare Modelle anwenden. Voraussetzung dazu
ist,
dass anstelle der unabhängigen Variablen der Gradient der
Kostenfunktion,
und anstelle des Kreuzprodukts aus unabhängigen Variablen die Hessematrix
der
Kostenfunktion betrachtet werden. Alle Wahrscheinlichkeitsaussagen, die sich
über
die Parameter treffen lassen, besitzen dann asymptotische Gültigkeit. Ihre
Bedeutung ist jedoch gegenüber linearen Modellen schwächer zu
bewerten, denn die Parameter sind in den nichtlinearen Modellen nicht in
eindeutiger Weise bestimmten Eingabevariablen zuweisbar (vergleiche Abschnitt
3.2.4.5). Darüber hinaus besitzen die Parameter der nichtlinearen Modelle
eine andere hypothetische Verteilung als die Parameter der linearen Modelle,
weshalb die Tests der linearen Modelle keine gültigen Aussagen
bezüglich der Signifikanz der Parameter von nichtlinearen Modellen
garantieren können. Für statistisch saubere Parameteranalysen
müssen daher Wald- und Lagrange-Multiplier-Tests herangezogen
werden, wie sie in Abschnitt 3.2.3 im Zusammenhang mit den Strategien zur
statistischen Modell-Selektion beschrieben wurden.
Durch die Funktionen von Neurometricus kann man für jeden Parameter
einzeln die Standardabweichung, das Vertrauensintervall und die Signifikanz
bestimmen. Dazu werden statistische Methoden eingesetzt, wie sie in Abschnitt
2.2 vorgestellt wurden. Ihre Vorgehensweise wird hier anhand eines für
nichtlineare Modelle modifizierten sogenannten Pseudo-t-Tests
beispielhaft vorgeführt:
-
Nullhypothese und Signifikanzniveau: Die zu prüfende Nullhypothese
des t-Tests ist "der Parameter i hat den Wert Null".
Das Sicherheitsniveau Alpha wird mit 0.05 vorgegeben, das bedeutet,
dass von 100 signifikanten Ablehnungen der Nullhypothese maximal 5 falsch
sein werden.
-
Prüfgrösse und Testverteilung bei Gültigkeit der
Nullhypothese: Als Prüfgrösse T dient beim
t-Test der Quotient des Parameters i und der Standardabweichung
des Parameters i. Durch diese Zusammensetzung ist T hypothetisch
t-verteilt mit v Freiheitsgraden, wobei v der um Eins
verringerten Anzahl der Beobachtungen der Eingabevariablen entspricht.
-
Kritischer Bereich: Beim t-Test liegt eine zweiseitige
Fragestellung vor, denn es wird geprüft, ob T in negativer oder
positiver Richtung signifikant von Null abweicht. Mithilfe der Tabelle der
t-Verteilung erkennt man bei v Freiheitsgraden und einem
Sicherheitsniveau von 0.05 für den kritischen Bereich den oberen Grenzwert
tcu auf negativer Seite, und den unteren Grenzwert tco auf
positiver Seite (vergleiche Abbildung 3.20).
-
Wert der Prüfgrösse: Anhand der Ergebnissen der
Schätzung kann der Wert der empirischen Prüfgrösse T
rechnerisch bestimmt werden.
-
Entscheidung und Interpretation: Die Nullhypothese wird abgelehnt, wenn
sich T innerhalb des kritischen Bereichs befindet, d.h. wenn T
kleiner als tcu oder grösser als tco ist. Man sagt in
diesem Fall, der Parameter i weicht signifikant von Null ab.
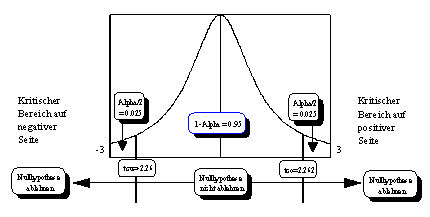
Abbildung 3.20: Testverteilung und kritischer Bereich
bei einem (Pseudo-)t-Test.
Quelle: Angelehnt an Bleymüller et al. (1988), S. 110.
Eine Möglichkeit, die Verteilung jedes einzelnen Parameters nach
mehrfacher Schätzung zu analysieren, ist mit der grafischen
Parameteranalyse von Neurometricus gegeben. Ein Beispiel hierfür wurde
bereits in Abschnitt 3.2.3 dargestellt. Dort wurden auch die damit eventuell
auftretenden Probleme beschrieben. Da die mit der Methode der kleinsten
Quadrate geschätzten Parameter jedoch unter bestimmten Annahmen
(vergleiche Abschnitt 3.2.4.4) biasfrei sind, stimmen ihre Erwartungswerte mit
den Parametern der Grundgesamtheit überein.
Die Robustheit eines einfach geschätzten Modells ergibt sich aus der
Streuung seiner Parameter. Um Aussagen über die Modellstabilität bei
Variation der Parameter treffen zu können, existiert in Neurometricus eine
Funktion namens nn_SW. Dabei werden die Parameter des neuronalen
Netzwerks in mehreren Durchgängen "geschüttelt", d.h.
zufällig innerhalb eines Vielfachen ihrer Standardabweichung modifiziert.
Anschliessend werden die ursprünglichen Ergebnisse der Approximation
und der Residuen mit den sich daraus ergebenden gemittelten Ergebnissen
grafisch überlagert.
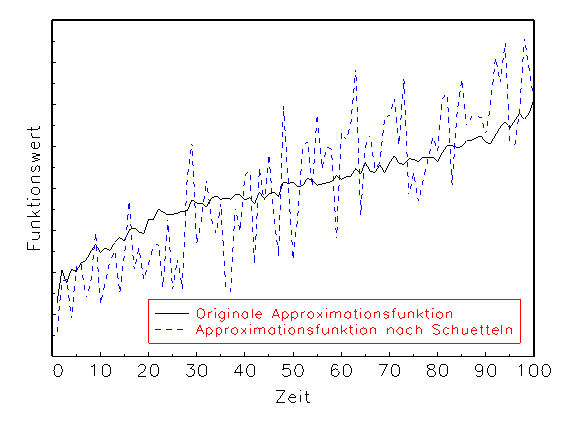
(a) Robustheitsanalyse-Diagramm der Approximation
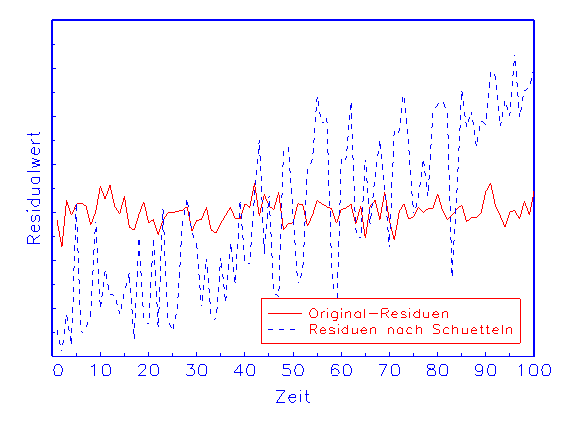
(b) Robustheitsanalyse-Diagramm der Residuen
Abbildung 3.21: Grafische Diagnose der Parameter bezüglich der Robustheit.
Das in Abbildung 3.21 gezeigte Ergebnis legt beispielsweise den Schluss
nahe, dass das betrachtete Modell bei gegebener Spezifikation und
Schätzung keine robusten Ergebnisse vorzuweisen hat, denn die Approximation
ändert sich durch die Modifikation der Parameter in unabsehbarer Weise.
Grosse Standardabweichungen der Parameter und die dadurch bedingten
Modellinstabilitäten sind häufig auf Kollinearitäten in den
Eingabevariablen zurückzuführen.
Wie in Abschnitt 2.3 erwähnt, besitzen die Ergebnisse einer linearen oder
nichtlinearen Schätzung, die auf der Methode der kleinsten Quadrate
basiert, nur dann Gültigkeit, wenn dem Modell bestimmte Annahmen
unterstellt werden können. Die Diagnose der Residuen ist eine
ex-post-Überprüfung dieser Modellannahmen. Sie kann in Form
statistischer Tests und grafischer Analysen (vergleiche Abbildung 3.22)
realisiert werden.
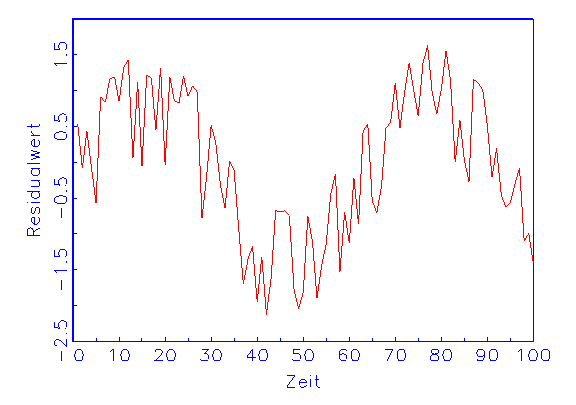
(a) Zeitreihen-Diagramm der Residuen |

(b) Histogramm der Residuen |
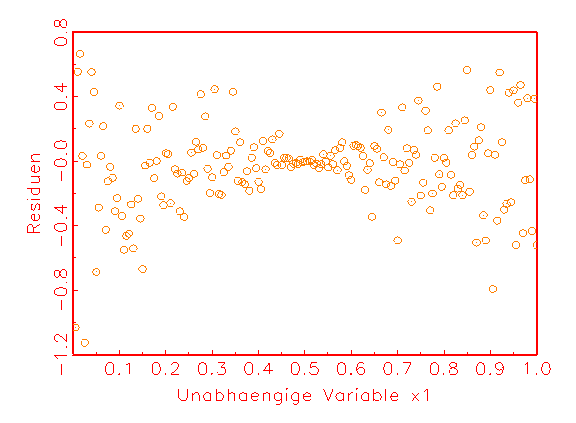
(c) Heteroskedastizitätsanalyse-
Diagramm der Residuen |
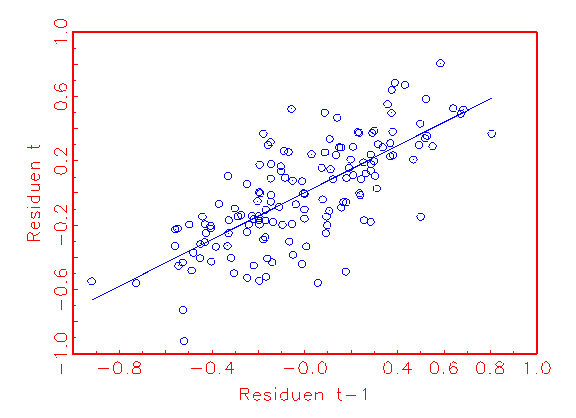
(d) Autokorrelationsanalyse-
Diagramm der Residuen |
Abbildung 3.22: Grafische Diagnose der Residuen verschiedener Modelle.
Grafische Zeitreihen von Residuen lassen eventuell vorhandene Strukturen
erkennen, die den Modellannahmen widersprechen (vergleiche Abbildung 3.22a).
Durch die Darstellung der Häufigkeitsverteilung der Residuen kann
geprüft werden, ob die Fehler in der geforderten Weise normalverteilt sind
mit einem Erwartungwert von Null. Diese Annahme ist bei dem in Abbildung 3.22b
gezeigten Beispiel nicht erfüllt.
Heteroskedastizitätsanalyse-Diagramme, die sich aus den Residuen und den
Beobachtungen der einzelnen Eingabevariablen zusammensetzen, kann man
verwenden, um das Bestehen von Heteroskedastizität in den Residuen
aufzudecken (vergleiche Abbildung 3.22c). Ob eine Korrelation der Residuen
untereinander vorliegt, lässt sich mithilfe von
Autokorrelationsanalyse-Diagrammen kontrollieren. Da die Regressionsgerade in
Abbildung 3.22d eine Steigung ungleich Null besitzt, liegt hier zum Beispiel
Autokorrelation vor.
Das Vorhandensein von Heteroskedastizität und/oder Autokorrelationen in
den Residuen führt zu einer beträchtlichen Unterschätzung der
tatsächlichen Standardabweichungen der Parameter. Wie sich mathematisch
beweisen lässt, sind in diesem Fall die geschätzten
Maximum-Likelihood-Parameter zwar immer noch erwartungstreu, aber nicht mehr
effizient.
In linearen Regressionsmodellen sind die einzelnen Parameter jeweils einer
bestimmten Eingabevariable zuweisbar. Die Grösse und
t-Statistik eines Parameters liefert einen Hinweis darauf, welche
Bedeutung die ihm zugeordneten Variable für die Güte der Regression
besitzt. Bei Einsatz von nichtlinearen Modellen ist die Möglichkeit einer
solchen Diagnose der Einflussgrössen nicht mehr gegeben, da hier
die Parameter eventuell Funktionswerte gewichten, die sich durch Summierung
mehrerer Eingabevariablen ergeben (vergleiche Abbildung 3.23).
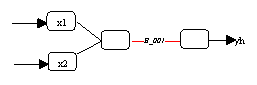
Abbildung 3.23: Zuordnung mehrerer Variablen zu einem Parameter.
Um dennoch Aussagen über die Bedeutung jeder einzelnen Eingabevariable
für die Güte der Approximation treffen zu können, wurden in
Neurometricus die folgenden zwei grafischen Analyseverfahren integriert:
Die Sensitivitätsanalyse liefert die schlüssigsten Ergebnisse, wenn
eine
Mittelwert-Varianz-Normierung der Variablen vorausgesetzt werden kann. Dadurch
variieren alle Beobachtungen der Eingabevariablen in einem Intervall von
ungefähr [-3,3]. Man kann dann jede Eingabevariable durch eine Sequenz von
Beobachtungen ersetzen, die sich gleichmässig über dieses
[-3,3]-Intervall erstrecken. Indem die restlichen, nicht betrachteten
Eingabevariablen konstant auf ihrem Mittelwert gehalten werden, lässt
sich die Approximation jeweils in Abhängigkeit der Beobachtungssequenz
berechnen und darstellen. Auf diese Weise gewinnt man einen Eindruck davon, wie
sensitiv die abhängige Variable auf eine Änderung der betrachteten
unabhängigen Variablen reagiert. Abbildung 3.24 zeigt dies an einem
Beispiel, bei dem eine Eingabevariable einen linearen Einfluss auf die
Approximation besitzt, während die zwei restlichen Eingabevariablen
nichtlinear in die Schätzung eingehen.
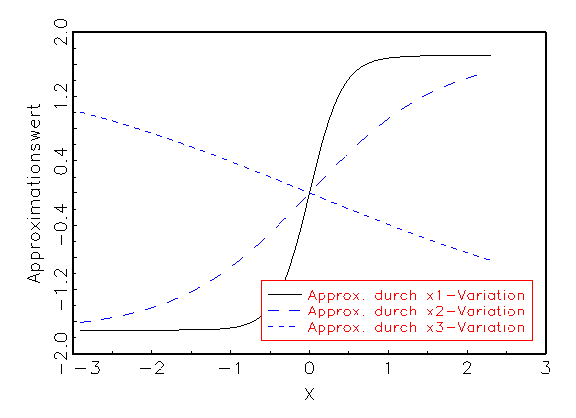
Abbildung 3.24: Grafische Diagnose der Variablen mithilfe
der Sensitivitätsanalyse.
Bei der Sensitivitätstrendanalyse wird die Approximation in
Abhängigkeit von nur einer Eingabevariable berechnet, indem diese
unverändert, die restlichen Variablen aber konstant auf dem Mittelwert
ihrer Beobachtungen gehalten werden. Man kann dann beobachten, ob der Verlauf
der sich daraus ergebenden Funktion tendenziell dem der wahren Funktion
entspricht. Auf diese Weise lassen sich zum Beispiel diejenigen
Eingabevariablen des Modells identifizieren, die die Güte der
Approximation eher mindern als verbessern. Ein Beispiel für den zuletzt
geschilderten Fall zeigt Abbildung 3.25b.
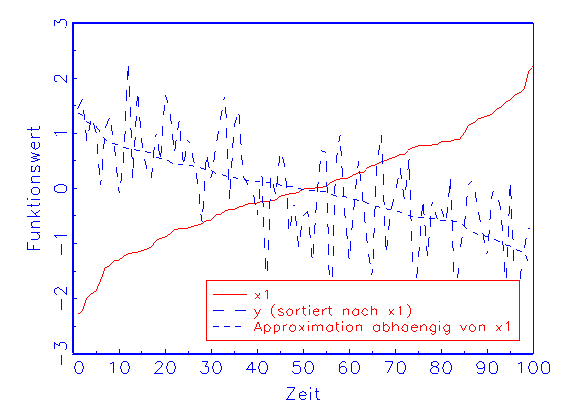
(a) Sensitivitätstrendanalyse-Diagramm für Variable x1
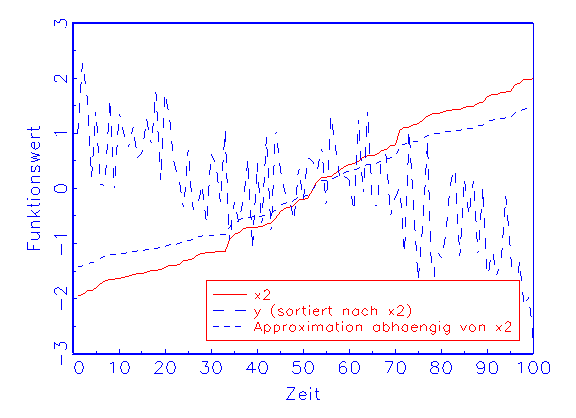
(b) Sensitivitätstrendanalyse-Diagramm für Variable x2
Abbildung 3.25: Grafische Diagnose der Variablen mithilfe
der Sensistivitätstrendanalyse.
Wie am Anfang des Abschnitts erwähnt, kann die Diagnose der Modellbildung
auf Basis einer einfachen Schätzung als auch auf Basis mehrfacher
Schätzungen erfolgen. Während im ersten Fall je Parameter nur ein
geschätzer Wert generiert wurde, steht im zweiten Fall je Parameter eine
Anzahl variierender Werte zur Verfügung (gesampelte Parameter). Die
gesampelten Parameter können zur Bildung von Häufigkeitsverteilungen
der Diagnose-Statistiken (vergleiche Abbildung 3.26), sowie zur Schätzung
von speziellen Vertrauensintervallen und speziellen Kovarianzmatrizen der
Parameter herangezogen werden.
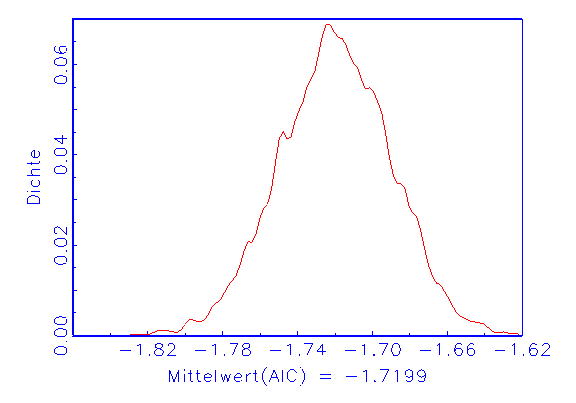
(a) AIC-Dichte
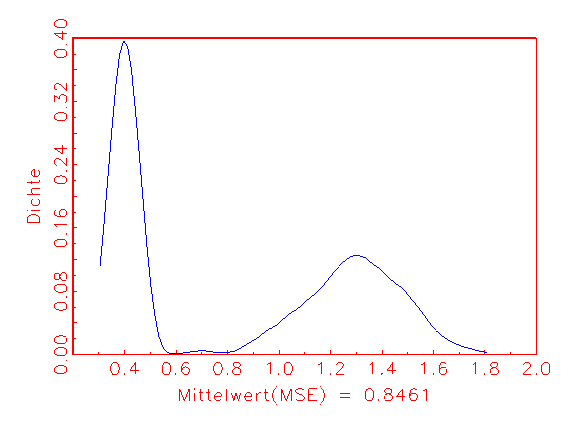
(b) MSE-Dichte
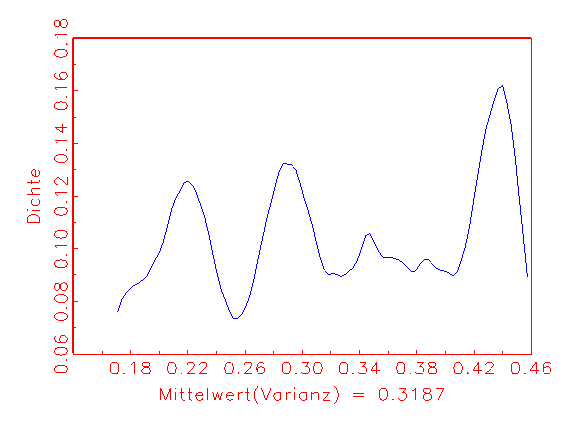
(c) Varianz-Dichte
Abbildung 3.26: Grafische Diagnose der Verteilung der Modellstatistiken.
Abbildung 3.26a zeigt die normalverteilte AIC-Dichte. Die bimodale MSE-Dichte
in Abbildung 3.26b verweist auf eine Kostenfunktion, deren Minima
bezüglich der Parameter relativ nahe beieinanderliegen. Durch
Einschränkung des Intervallbereichs bei der Zufallsinitialisierung der
Parameter kann eventuell ein konsistenteres Bild erzeugt werden. Der chaotische
Verlauf der Varianz-Dichte in Abbildung 3.26c lässt ein
fehlspezifiziertes Modell vermuten, da der Erwartungswert der Varianz nicht in
einem Punkt kollabiert.