Diplomarbeit - Konstruktion von NN für Regressionsanalysen - Kapitel 3.3
von Daniel Schwamm (09.11.2000)
In diesem Abschnitt wird die Leistungsfähigkeit des neurometrischen
Ansatzes anhand einer real gegebenen ökonomischen Problemstellung
demonstriert. Untersucht wird ein vermuteter Zusammenhang zwischen mehreren
empirisch erhobenen Variablen, wie er sich aus der Theorie der Insolvenz
ableiten lässt. Als Vergleichsbasis dient die herkömmliche
multiple lineare Diskriminanzanalyse.
Seit drei Jahren wird vom Statistischen Bundesamt ein Anstieg der Konkurse und
Vergleiche in West- und Ostdeutschland beobachtet. Die Insolvenzen haben
inzwischen ein Ausmass angenommen, bei dem nicht mehr von einem
"gesunden" Ausleseprozess für die Marktwirtschaft
gesprochen werden kann, der leistungsfähige Betriebe erhält und
weniger leistungsfähige aus dem Markt auscheiden lässt. Der
gesamtwirtschaftliche Schaden wird alleine für das erste Halbjahr 1995 auf
14 Milliarden DM beziffert. In diesem Klima meiden Banken zunehmend Risiken bei
der Vergabe von Krediten, worunter vor allem kleine und mittelständische
Unternehmen zu leiden haben. Es ist daher notwendig, Analyseverfahren zu
entwickeln, die es ermöglichen, die Kreditwürdigkeit von Kunden
anhand ihrer Überlebenswahrscheinlichkeit zu überprüfen.
In der Literatur werden als wichtige Einflussgrössen der
Insolvenz häufig die Grösse und das Alter von Unternehmen
genannt. Aus evolutionstheoretischen Ansätzen lassen sich die folgenden
hypothetischen Zusammenhänge konstruieren: Neugegründete Unternehmen
haben Legitimationsprobleme gegenüber ihrer Umwelt, weswegen sie
vergleichsweise oft aus dem Markt ausscheiden
(Liability-of-Newness-Hypothese). In der
Liability-of-Aging-Hypothese wird behauptet, dass die
Inflexibilität eines Betriebs mit steigendem Alter zunimmt, was das
Sterberisiko erhöht. Auch der Verbrauch der Gründungsressourcen kann
dazu führen, dass das Insolvenzrisiko eines Unternehmens steigt
(Liability-of-Adolescene-Hypothese). Der Sachverhalt, dass kleine
Unternehmen mit grösserem Sterberisiko behaftet sind als grosse
Unternehmen, wird mit der Liability-of-Smallness-Hypothese
ausgedrückt.
Die folgende empirische Untersuchung wurde von A. Szczesny, O. Korn und dem
Verfasser im Rahmen einer Projektarbeit im ZEW durchgeführt. Dabei wurde
auf die in Abschnitt 3.1 vorgestellte Software und den in Abschnitt 3.2
erläuterten neurometrischen Modellbildungsprozess
zurückgegriffen. Die Ergebnisse sind im ZEW Newsletter Nr. 2, Dezember
1995, unter dem Titel "Insolvenzanalyse mit Neuronalen Netzwerken"
veröffentlicht worden.
Bei der Datenidentifikation stand ein Datensatz mit Informationen von rund
10.000 Unternehmen aus dem MUP des ZEW zur Verfügung. Beim MUP handelt es
sich um ein von der Stiftung Volkswagenwerke gefördertes Projekt, dessen
Ziel es ist, die Entwicklung bundesdeutscher Unternehmen über die Zeit zu
verfolgen. Die Unternehmensdaten sind dem Datensatz der deutschen
Kreditauskunftei Verband der Vereine Creditreform (VVC) entnommen worden. Als
unabhängige Variablen wurden die Grösse und das Alter, als
abhängige Variable die Insolvenzwahrscheinlichkeit der Unternehmen
definiert. Ziel war die Erklärung eines Zusammenhang zwischen diesen
Grössen. Nach Selektion und Gruppierung der betrachteten Daten ergab
sich die in Abbildung 3.27 angegebene dreidimensionale Verteilung der realen
Beobachtungen der Variablen.

Abbildung 3.27: Relative Häufigkeit der reale Beobachtungen
je Variablen- und Klasseneinteilung.
Quelle: Szczesny/Korn (1995), S. 14.
Als erstes Modell wurde das aus der Statistik bekannte Logit-Modell
spezifiziert. Es handelt sich hierbei um ein multiples, lineares
Regressionsmodell mit einer Konstanten als zusätzlicher
Einflussgrösse (vergleiche Abbildung 3.28a). Die
Wahrscheinlichkeiten der Insolvenz der betrachteten 27 Klassen sind in
sogenannte Logits umgerechnet worden. Nach Schätzung der Parameter des
Modells wurde die in Abbildung 3.28b gezeigte Approximation des gesuchten
Zusammenhangs zurückgeliefert. Man erkennt, dass der beobachtete
Anstieg der Insolvenzen nach 30 bis 40 Jahren bei kleineren Unternehmen nicht
korrekt wiedergegeben wird.
(a) Spezifikation des Logit-Modells
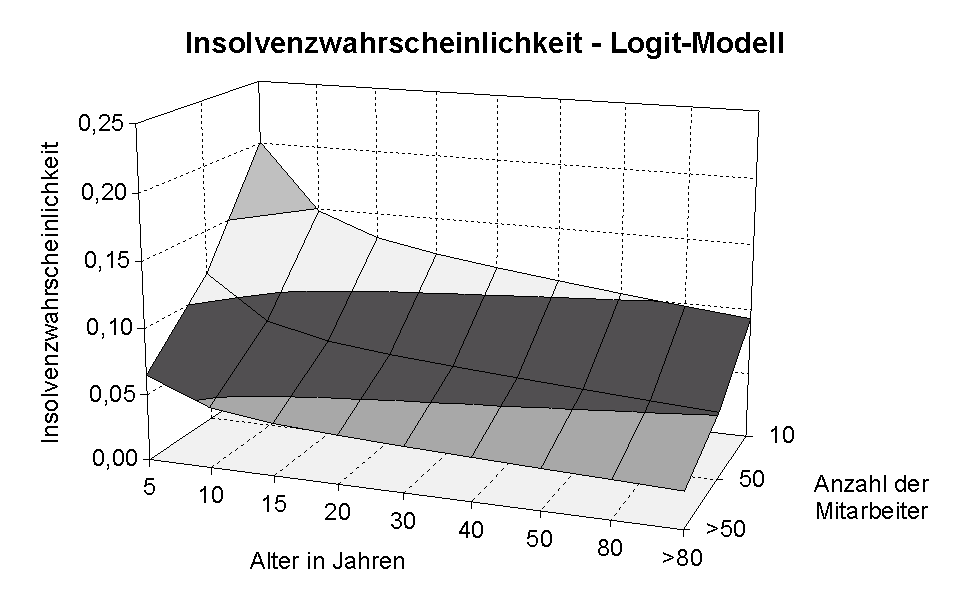
(b) Approximation des Logit-Modells
Abbildung 3.28: Herkömmliche Diskriminanzanalyse.
Quelle: Szczesny/Korn (1995), S. 14.
Danach wurden vom Verfasser mithilfe der Funktionen, die Neurometricus
bereitstellt, eine neurometrische Untersuchung des unbekannten Zusammenhangs
zwischen den betrachteten Variablen durchgeführt. Die Ergebnisse werden im
folgenden beschrieben.
Im Rahmen der Datenidentifikation wurde zunächst eine grafischen Analyse
der
betrachteten Variablen vorgenommen. Wie in Abbildung 3.29 gezeigt wird, wurden
dabei
keine der in Abschnitt 2.3.1 beschrieben Datenprobleme beobachtet. Es steht
y_001 für die Logits, x_001 für die Grösse
und x_002 für das Alter der Unternehmen. Das Zeitreihen-Diagramm
weist
die betrachteten Variablen als stationär aus, da sie um einen Mittelwert
streuen (vergleiche Abbildung 3.29a). Wie dem
Kollinearitätsanalyse-Schaubild in Abbildung 3.29b zu entnehmen ist, wird
der Eigenraum vollständig aufgespannt, weswegen die unabhängigen
Variablen als linear unabhängig voneinander angenommen werden können.
Es lassen sich ausserdem auch keine Ausreisser in den Histogrammen
der betrachteten Variablen erkennen (vergleiche Abbildung 3.29c/d/e). Auf eine
Teilung und Normierung der Datensätze wurde verzichtet, da hierfür
zuwenig Beobachtungen zur Verfügung standen und die numerischen Ränge
der Beobachtungen der Variablen relativ ähnlich zueinander sind.

(a) Zeitreihen-Diagramm der
betrachteten Variablen |

(b) Zweidimensionales Kollinearitätsanalyse-Schaubild der unabhängigen Variablen |

(c) Histigramm der Logits
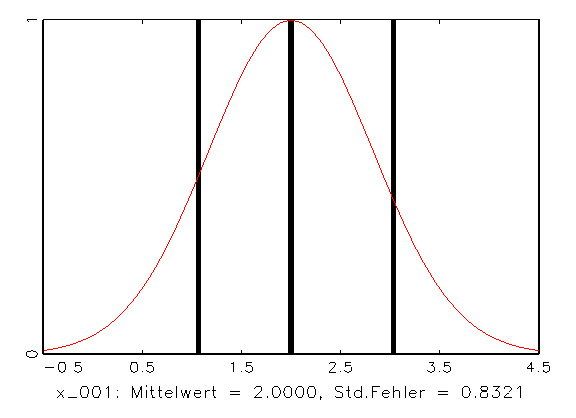
(d) Histogramm der Grösse |

(e) Histogramm des Alters |
Abbildung 3.29: Datenidentifikation der Insolvenzanalyse.
Gemäss der in Abschnitt 3.2.2 beschrieben Vorgehensweisen der
Strategien
zur statistischen Modell-Selektion wurde danach im Rahmen der Spezifikation
zunächst ein Basismodell gebildet. Dessen Struktur orientierte sich an dem
Logit-Modell der Diskriminanzanalyse, jedoch wurde auf die lineare konstanten
Einflussgrösse verzichtet. Anschliessend wurden alle in
Neurometricus integrierten Strategien zur statistischen Modell-Selektion
jeweils zehnmal hintereinander ausgeführt. Dabei ergaben sich die in
Abbildung 3.30 gezeigten Spezifikationen von neuronalen Netzwerken mit den in
Tabelle 3.1 angegebenen Häufigkeiten. Als Aktivierungsfunktion wurde in
jedem Fall der Tangens hyperbolicus verwendet. Auf die abhängige Variable
wurde ein zusätzlicher normalverteilter Störterm gegeben, um einer
singulären Kovarianz der Parameter vorzubeugen. Die nichtlineare
Konstante, die in Modells 3 eingeht, war bei jeder Schätzung aktiviert,
wurde aber nur dort als signifikant anerkannt.
(a) Spezifikation von Modell 1
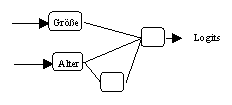
(b) Spezifikation von Modell 2
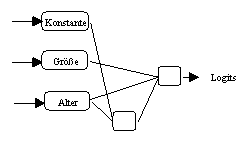
(c) Spezifikation von Modell 3
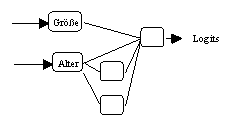
(d) Spezifikation von Modell 4
Abbildung 3.30: Spezifikationen der selektierten Modelle.
| Strategien zur statistischen Modell-Seketion |
Häufigkeit Modell 1 |
Häufigkeit
Modell 2 |
Häufigkeit Modell 3 |
Häufigkeit
Modell 4 |
| White-Strategie |
0 |
6 |
4 |
0 |
| Teräsvirta-Strategie |
2 |
4 |
4 |
0 |
| AIC-Strategie |
2 |
5 |
3 |
0 |
| SIC-Strategie |
3 |
5 |
2 |
0 |
| NIC-Strategie |
1 |
5 |
3 |
1 |
| Summe |
8 |
25 |
16 |
1 |
Tabelle 3.1: Häufigkeit der selektierten Modelle.
Aufschlussreich an den selektierten Modellen ist vor allem der
Sachverhalt, dass alleine für das Alter ein nichtlinearer
Einfluss auf die Wahrscheinlichkeiten der Insolvenz als statistisch
gesichert festgestellt worden ist. Dieses Ergebnis lässt sich im
Rahmen der Theorie der Insolvenz plausibel durch die oben aufgeführten
Liability-of-...-Hypothese erklären, von denen es bezüglich
der Grösse nur eine und bezüglich des Alters insgesamt drei
gibt.
Bei der anschliessenden Diagnose wurden die Ergebnisse des
herkömmlichen Logit-Modell mit denen des neurometrischen Modells 2
verglichen. Zuvor wurde der Störterm der abhängigen Variable
entnommen und das Modell 2 neu geschätzt. Abbildung 3.31 zeigt die
Regressions-Diagramme der diagnostizierten Modelle, wobei jeweils mit
yhat_001 die Approximation der abhängigen Variable y_001
gekennzeichnet wurde. Wie zu erkenne ist, besitzt die Approximation in
Abbildung 3.31b einen kleineren Bias und eine kleinere Varianz als die
Approximation in Abbildung 3.31b.
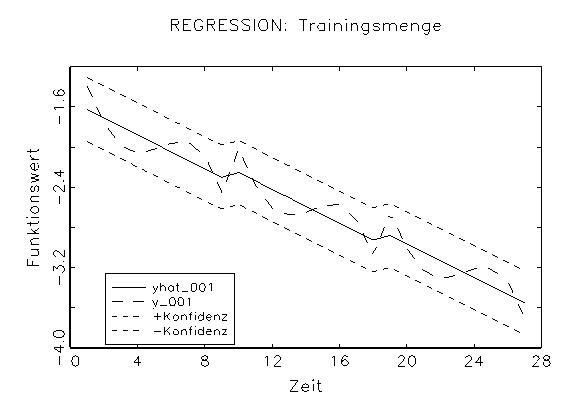
(a) Regressions-Diagramm des Logit-Modells
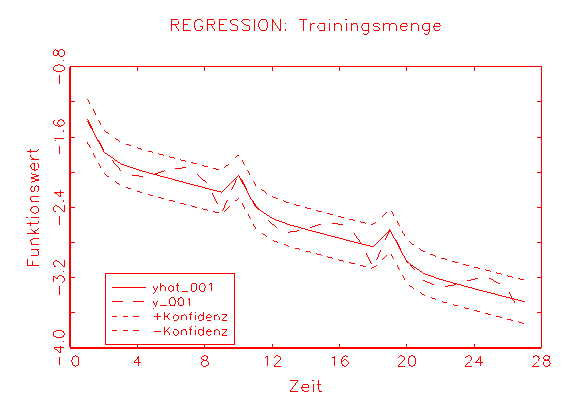
(b) Regressions-Diagramm des Modells 2
Abbildung 3.31: Regressions-Diagramme der diagnostizierten Modelle.
Mithilfe von XY-Streuungs-Diagrammen, bei denen die Beobachtungen von
y_001 gegen die Beobachtungen von yhat_0001 in das kanonische
Koordinatensystem eingetragen wurden, kann die höhere Qualität der
Approximation des Modells 2 gegenüber der Approximation des Logit-Modells
ebenfalls demonstriert werden: In Abbildung 3.32a streuen die
(y_001/yhat_001)-Punkte stärker um die gestrichelt eingezeichnete
Regressionsgerade als in Abbildung 3.32b.

(a) XY-Steuungsdiagramm mit
Regressionsgerade des Logit-Modells |
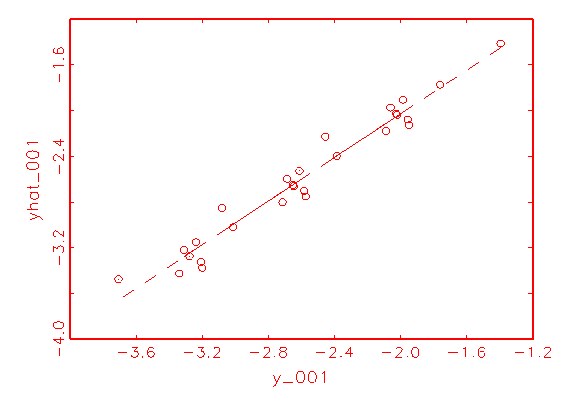
(b) XY-Streuungsdiagramm mit
Regressionsgerade des Modells 2 |
Abbildung 3.32: (y_001/yhat_001)-Streuungs-Diagramme der betrachteten Modelle.
Abbildung 3.33 zeigt die Ergebnisse der grafischen Diagnose der Residuen der
betrachteten Modelle. Die Zeitreihen-Diagramme der Residuen und die Histogramme
der
Residuen weisen aus, dass die Residuen in beiden Fällen einen
Erwartungswert
von Null besitzen, jedoch ist die Varianz der Residuen des Modells 2 kleiner
als die
Varianz der Residuen des Logit-Modells (vergleiche Abbildung 3.33c/d und
Abbildung
3.33a/b). In Abbildung 3.33e und Abbildung 3.33f ist zu erkennen, dass die
Autokorrelation der Residuen in beiden Fällen nicht beseitigt wurde, da
die eingezeichnete Regressionsgerade eine Steigung ungleich Null besitzt. Im
Fall des Modells 2 ist dies wohl darauf zurückzuführen, dass mit
27 Beobachtungen je betrachteter Variable zuwenig Daten zur Verfügung
standen, um eine Spezifikation zu finden, die keine Autokorrelation der
Residuen mehr besitzt. Denn wie in Abschnitt 3.2.2.3 beschrieben wurde,
können die Strategien zur statistischen Modell-Selektion nur dann
statistisch gesicherte Ergebnisse hervorbringen, wenn die geschätzten
Parameter einer (asymptotischen) Normalverteilung gehorchen. Als Faustregel
gilt jedoch, dass bei unabhängigen, identisch verteilten
Zufallsvariablen wie den Parametern erst ab Stichprobenumfänge
grösser 30 eine asymptotische Normalverteilung ihres arithmetischen
Mittels angenommen werden kann.
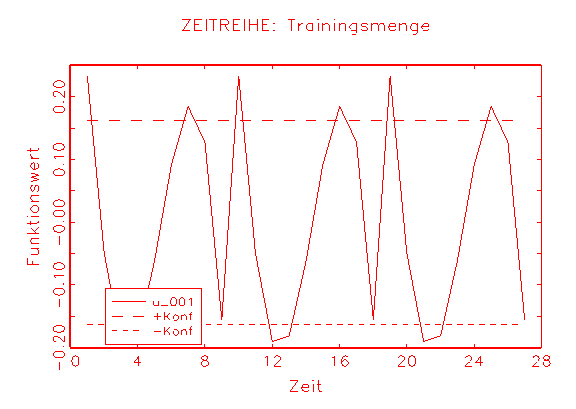
(a) Zeitreihen-Diagramm der Residuen
des Logit-Modells |

(b) Zeitreihen-Diagramm der Residuen
des Modells 2 |

(c) Histogramm der Residuen des Logit-Modells |
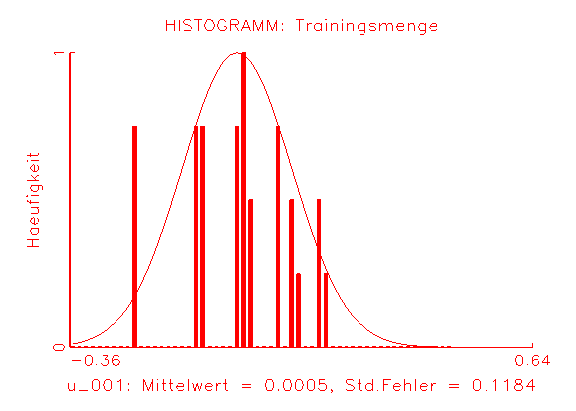
(d) Histogramm der Residuen des Modells 2 |
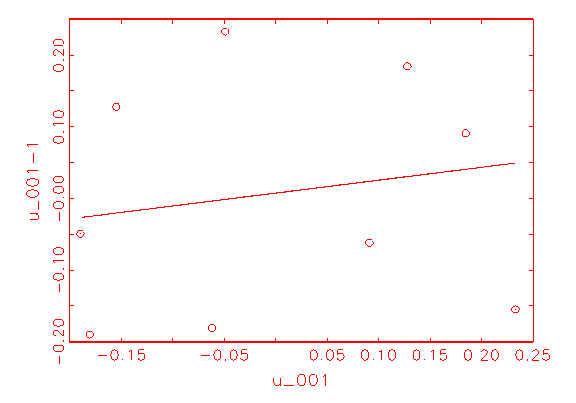
(e) Autokorrelationsanalyse-Diagramm
des Logit Modells |

(f) Autokorrelationsanalyse-Diagramm
des Modells 2 |
Abbildung 3.33: Grafische Diagnose der Residuen der betrachteten
Modelle.
Durch die Diagnose des Einflusses der unabhängigen Variablen auf die
Approximation des zugrunde liegenden Modells kann noch einmal der nichtlineare
Einfluss der Grösse auf die Logits hervorgehoben werden.
Abbildung 3.34a zeigt das Sensitivitätsanalyse-Diagramm des Logit-Modells,
wobei x__001 die Konstante, x_002 die Grösse und
x_003 das Alter kennzeichnen, und Abbildung 3.34b zeigt das
Sensitivitätsanalyse-Diagramm des Logit-Modells, wobei x__001 die
Grösse und x_002 das Alter kennzeichnen. Anhand der
Sensitivitätsanalyse-Diagramme wird dagegen erkennbar, dass die
unabhängigen Variablen in beiden Fällen die Approximation tendenziell
fördern und daher nicht ohne eine unnötige Biaserzeugung aus den
Modellen entnommen werden können (vergleiche Abbildung 3.34c/e und
Abbildung d/f).

(a) Sensitivitätsanalyse-Diagramm
des Logit-Modells |
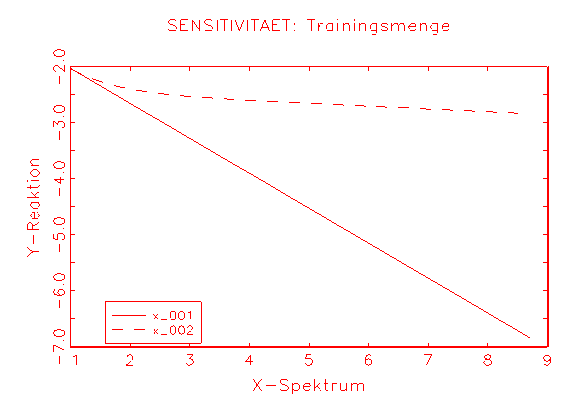
(b) Sensitivitätsanalyse-Diagramm
des Modells 2 |
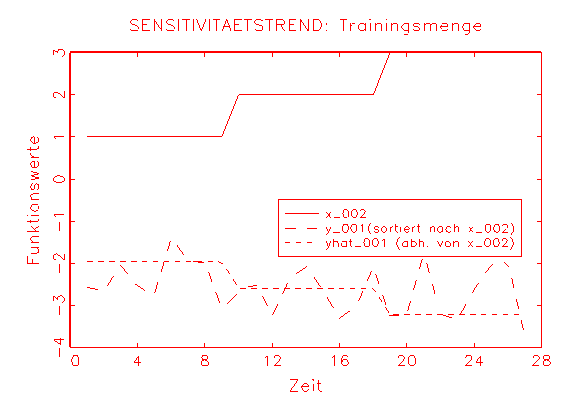
(c) Sensitivitätstrendanalyse-Diagramm
des Alters des Logit-Modells |

(d) Sensitivitätstrendanalyse-Diagramm
des Alters des Modells 2 |
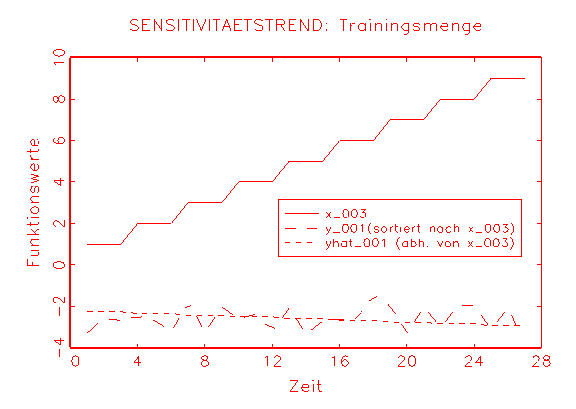
(e) Sensitivitätstrendanalyse-Diagramm
der Grösse des Logit-Modells |

(f) Sensitivitätstrendanalyse-Diagramm
der Grösse des Modells 2 |
Abbildung 3.34: Grafische Diagnose des Einflusses der unabhängigen
Variablen auf die Approximation der betrachteten Modelle.
Die grafische Diagnose der Verteilung der von den betrachteten Modellen
erbrachten Statistiken wurde am Beispiel des MSE vorgenommen. Dazu wurden
jeweils 25 Bootstrap-, 25 Jackknife- und 25 Cross
Validation-Schätzungen durchgeführt. Die so gebildeten
MSE-Dichten zeigen in allen Fällen, dass die MSE-Varianzen des
Modells 2 etwas grösser, aber die MSE-Erwartungswerte annähernd
um die Hälfte kleiner sind als beim Logit-Modell (vergleiche Abbildung
3.35b/d/f und Abbildung 3.35a/c/e).
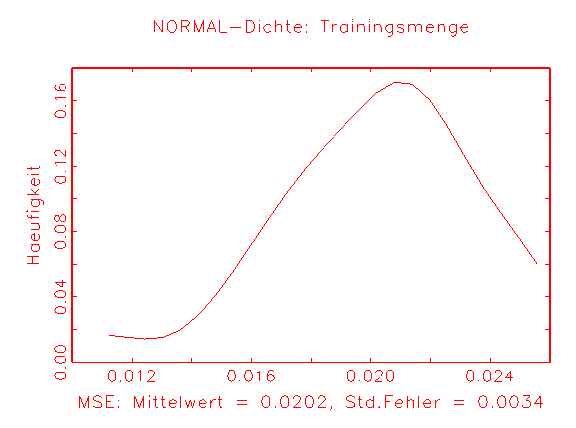
(a) MSE-Dichte des Logit-Modells nach
25 Bootstrap-Schätzungen |
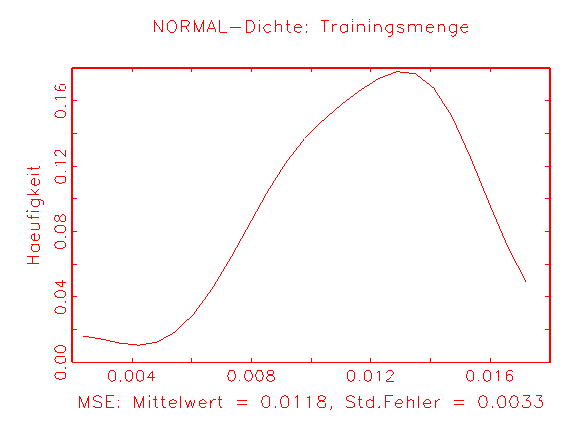
(b) MSE-Dichte des Modells 2 nach
25 Bootstrap-Schätzungen |
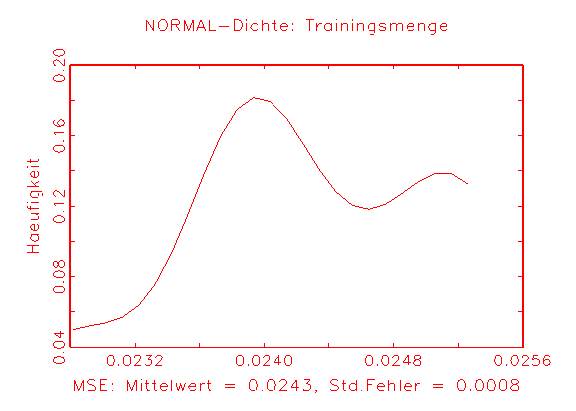
(a) MSE-Dichte des Logit-Modells nach
25 Jackknife-Schätzungen |

(b) MSE-Dichte des Modells 2 nach
25 Jackknife-Schätzungen |
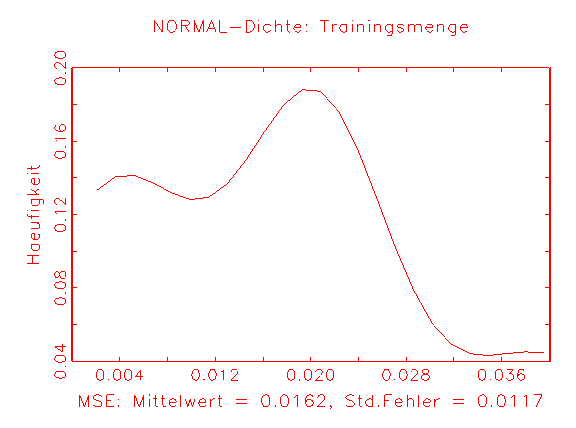
(a) MSE-Dichte des Logit-Modells nach
25 Cross Validation-Schätzungen |

(b) MSE-Dichte des Modells 2 nach
25 Cross Validation-Schätzungen |
Abbildung 3.35: Grafische Diagnose der Verteilung des MSE der
betrachteten Modelle.
Als letztes Diagnoseverfahren wurde noch eine grafische Analyse der Robustheit
des Modells 2 vorgenommen. Auf eine Robustheitsanalyse des Logit-Modells wurde
verzichtet, da ein Vergleich beider Modelle in diesem Punkt nicht
"fair" sein würde, denn die Stabilität eines Modells
hängt nicht nur von der Standarabweichung seiner Parameter ab, sondern
auch von der Anzahl der Parameter. Abbildung 3.36 zeigt, dass das Model 2
nach Variation der Parameter innerhalb ihrer Standardabweichung kaum
Änderungen bezüglich der Approximation und den sich dadurch
ergebenden Residuen aufweist. Dieses Ergebnis deutet auf ein robustes Modell
hin.
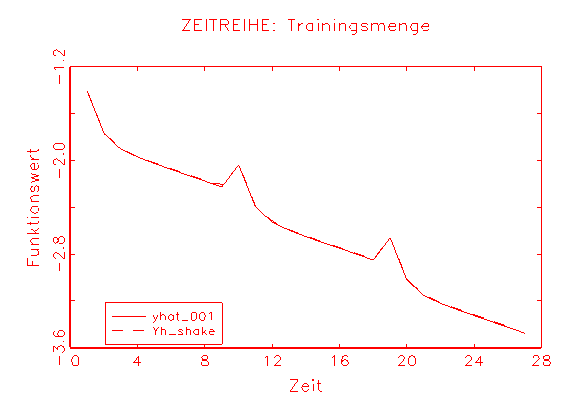
(a) Robustheitsanalyse-Diagramm
der Approximation |

(b) Robustheitsanalyse-Diagramm
der Residuen |
Abbildung 3.36: Grafische Diagnose der Robustheit des Modells 2.
Bei der obigen Untersuchung wurden bisher nur die grafischen Ergebnisse
wiedergegeben, die sich durch den Vergleichs des herkömmlichen
Logit-Modells mit dem neurometrischen Modell 2 ergeben haben. Aber auch
gemessen an den Gütemassen, Informationskriterien,
Prognosequalitätsmassen usw., die von Neurometricus berechnet
wurden, ging das Modell 2 gegenüber dem Logit-Modell als
"Punktesieger" hervor. Der Vollständigkeit halber werden einige
der berechneten Statistiken in Tabelle 3.2 aufgeführt. Da sich die aus den
Statistiken ableitbaren Informationen mit denen der grafischen Ergebnisse
decken, wird hier auf ihre separate Interpretation verzichtet.
| Modellstatistik |
Wert des Logit-Modells |
Wert des Modells 2 |
| AIC |
-0.6889 |
-1.1705 |
| SIC |
-0.5644 |
-0.9785 |
| 2×NIC |
-0.8728 |
-1.4204 |
| R2 |
0.9291 |
0.9593 |
| R2 justiert |
0.9231 |
0.9540 |
| Prediction Criterion |
0.9706 |
0.9818 |
| Final Prediction Error |
0.0294 |
0.0182 |
| SSE |
0.6356 |
0.3646 |
| MSE |
0.0235 |
0.0135 |
| Root MSE |
0.1534 |
0.1162 |
| Mean Absolute Error |
0.0141 |
0.0905 |
| Mean Absolute Percent Error |
5.8521 |
3.4634 |
Tabelle 3.2: Gegenüberstellung der Statistiken der betrachteten Modelle.
Abbildung 3.37 zeigt noch einmal, dass der wahre Zusammenhang zwischen den
betrachteten Variablen mithilfe des neuronalen Netzwerks besser approximiert
worden ist als mit dem linearen Logit-Modell: Insbesondere der beobachtete
Anstieg der Insolvenzen nach 30 bis 40 Jahren bei kleineren Unternehmen wird
von der neurometrischen Approximation korrekt wiedergegeben. Damit erweisen
sich neuronale Netzwerke, die über eine statistisch fundierte
Spezifikation verfügen, als geeigneter zur Prognose von Insolvenzen und
Kreditausfallrisiken als statistische Standardverfahren wie das Logit-Modell.
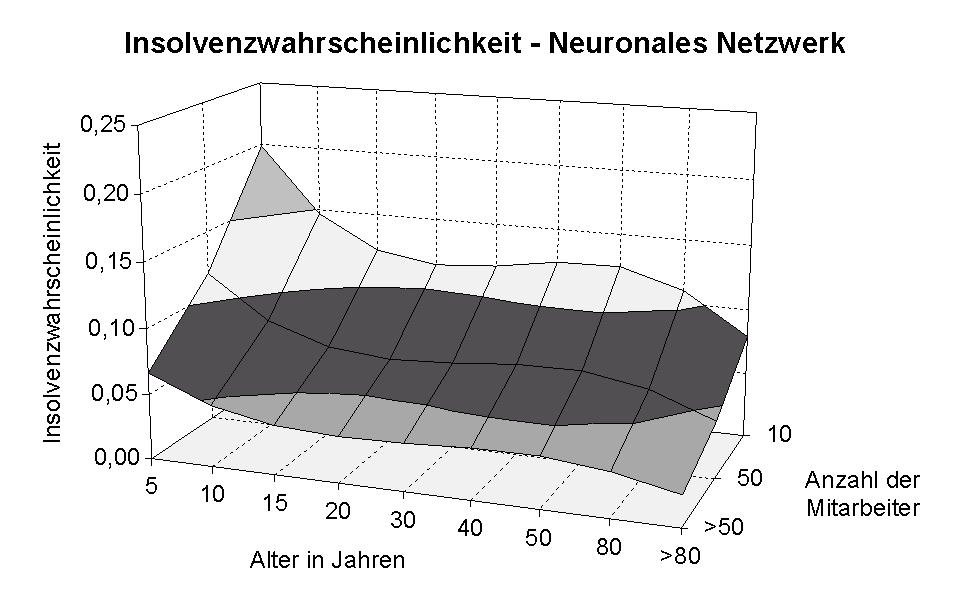
Abbildung 3.37: Approximation des neuronalen Netzwerks.
Quelle: Szczesny/Korn (1995), S. 14.