Diplomarbeit - Konstruktion von NN für Regressionsanalysen - Kapitel 2.1
von Daniel Schwamm (09.11.2000)
In diesem Abschnitt wird der Begriff neuronales Netzwerk definiert und ein
Schema vorgeschlagen, mit dessen Hilfe sich die verschiedenen Typen von
neuronalen Netzwerken voneinander abgrenzen lassen. Auf diese Weise können
diejenigen Modelle durch Nennung der Klassifizierungskriterien charakterisiert
werden, die für die Problemstellung der vorliegenden Arbeit relevant
erscheinen. Eine vertiefte Betrachtung der Thematik, insbesondere die
Beschreibung der Stärken und Schwächen der einzelnen Modelltypen
sowie die Darstellung der Analogien zwischen neuronalen Netzwerken und
(menschlichen) Gehirnen, findet bei Niedereichholz/Mechler (1992), Lawrence
(1992) und Kruse et al. (1991) statt.
Als neuronale Netzwerke bezeichnet man aus einfachen (adaptiven) Bausteinen
zusammengesetzte, massiv parallele Verbundnetzwerke, deren Struktur und
Arbeitsweise dem natürlichen Vorbild des Nervensystems angelehnt ist. Ihre
Architektur soll dadurch zur Nachbildung biologischer Intelligenz in
künstlichen Systemen potenziell besser geeignet sein, als die sequenziell
organisierte von-Neumann-Architektur herkömmlicher Computer. Die
Neuroinformatik verfolgt das Ziel, so komplexe menschliche Fähigkeiten wie
"Intelligenz" und "selbstständige Problemlösung" in
neuronalen Netzwerken zu implementieren. Diesen Anspruch erfüllen
neuronalen Netzwerke (bisher) nicht. Wie sie auch heute schon leistungsstark
eingesetzt werden können, wird in Kapitel 3 vorgeführt werden.
Es gibt eine Vielzahl verschiedener Typen von neuronalen Netzwerken. Wie im
folgenden gezeigt wird, können sie zur Vereinfachung durch die drei
Kriterien Neuronentyp, Topologie und Lernverfahren klassifiziert und
charakterisiert werden.
Die Neuronen eines künstlichen neuronalen Netzwerks haben die Aufgabe, in
spezifischer Weise Eingabesignale zu Ausgabesignale zu verarbeiten. Der
Transformationsprozess innerhalb eines Neurons ist in Abbildung 2.1
schematisch veranschaulicht: Die Eingabesignale werden beim Eintritt in das
Neuron jeweils gewichtet, zu einem Gesamtsignal aufsummiert, danach
(nicht-)linear transformiert und schliesslich als Ausgabesignal wieder
nach aussen abgegeben. Da das beschriebene Verarbeitungsprinzip
Allgemeingültigkeit für alle künstlichen Neuronen besitzt, ist
durch die Anzahl der vorgeschalteten Gewichte, die Propagierungsfunktion und
die Aktivierungsfunktion der Typ eines Neurons vollständig determiniert.
Die verwendeten Begriffe werden im Folgenden definiert.
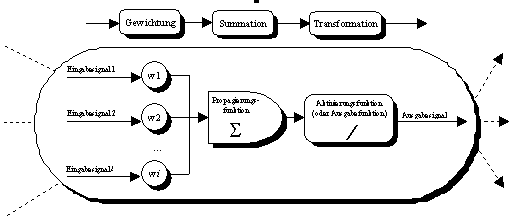
Abbildung 2.1: Transformationsprozess innerhalb eines (versteckten) Neurons.
Quelle: Angelehnt an Niedereichholz/Mechler (1992), S. 9.
Durch sogenannte Gewichte werden Signale, die zwischen den Neuronen eines
künstlichen neuronalen Netzwerks ausgetauscht werden, gezielt
verstärkt oder geschwächt. Neuronen, die über keine
vorgeschalteten Gewichte verfügen, bezeichnet man als Eingabeneuronen.
Analog dazu bezeichnet man Neuronen ohne nachgeschaltete Gewichte als
Ausgabeneuronen. Alle anderen Neuronen sind versteckte Neuronen. Der
beschriebene Transformationsprozess innerhalb eines Neurons wird im hohen
Masse durch die vorgeschalteten Gewichte beeinflusst.
Die Propagierungsfunktion berechnet (in der Regel durch einfache Summation) den
Nettoinput eines Neurons aus den gewichteten inhibitorischen und exitatorischen
Signalen. Der Nettoinput wird (je nach zugrunde liegendem Neuronenmodell mit dem
aktuellen Aktivierungszustand des Neurons aufaddiert) an die
Aktivierungsfunktion übergeben, wodurch der neue Aktivierungszustand des
Neurons bestimmt wird. Gegebenenfalls muss der Aktivierungszustand einen
vorher festgelegten Schwellenwert übertreffen, um als Ausgabesignal nach
aussen abgegeben zu werden. Man sagt, ein Neuron "feuert", falls
es ein Ausgabesignal liefert. In der Literatur wird der Begriff Ausgabefunktion
nicht einheitlich definiert, aber in dieser Arbeit wird darunter die
Aktivierungsfunktion der Ausgabeneuronen verstanden.
Eine Auswahl möglicher Aktivierungsfunktionen zeigt Abbildung 2.2.
Unterschieden werden unter anderem lineare und nichtlineare, analoge und
diskrete, differenzierbare und nicht-differenzierbare, mit und ohne Schwellwert
behaftete, sowie deterministische und stochastische Funktionen. Sie besitzen
jeweils typische Eigenschaften, die sich in spezifischer Weise auf den
Transformationsprozess innerhalb des Neurons auswirken. Welche
Aktivierungsfunktion die beste ist, hängt von der Art des durch das
neuronale Netzwerk zu lösenden Problems ab.

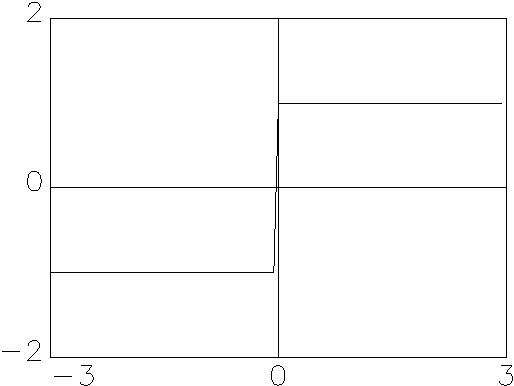
| (a) Lineare Funktion |
(b) Signum-Funktion |

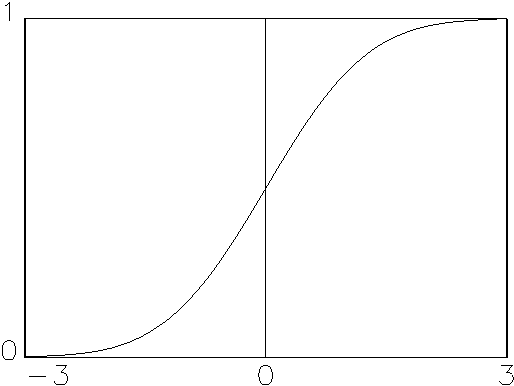
| (c) Tangens Hyperbolicus |
(d) Logistische Funktion |

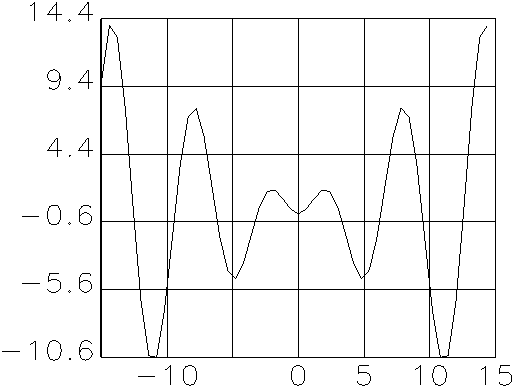
| (e) Quadratische Funktion |
(f) X×Sinus-Funktion |
Abbildung 2.2: Auswahl möglicher Aktivierungsfunktionen.
Quelle: Angelehnt an Anders (1993), S. 3.
Ohne darauf an dieser Stelle näher eingehen zu können, sei
erwähnt, dass auch die zur Verfügung stehenden Daten und das
später erläuterte Lernverfahren die Wahl der Aktivierungsfunktion
einschränken. Im Prinzip gilt, dass jede Aktivierungsfunktion ein
eigenes theoretisches Modell des Neurons darstellt.
Die Topologie eines neuronalen Netzwerks gibt an, wie die Verbindungsstruktur
zwischen den Neuronen aufgebaut ist. Typ-gleiche Neuronen lassen sich zu
sogenannten Schichten zusammenfassen. In Analogie zum Typ der Neuronen, aus
denen eine Schicht besteht, unterscheidet man die Eingabeschicht, die
Ausgabeschicht und die versteckten Schichten. Neuronen innerhalb
derselben Schicht tauschen untereinander keine Signale aus. Von schichtlosen
neuronalen Netzwerk spricht man, wenn jedes Neuron mit jedem anderen verbunden
ist.

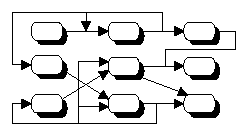
(a) Vorwärtsgekoppeltes Netzwerk
mit drei Schichten |
(b) Rückwärtsgekoppeltes Netzwerk
ohne Schichten |
Abbildung 2.3: Topologien von neuronalen Netzwerken.
Quelle: Angelehnt an Niedereichholz/Mechler (1992), S. 10.
Die Topologie legt auch fest, ob die Aktivierungsausbreitung innerhalb des
neuronalen Netzwerk in nur eine Richtung oder in mehreren Richtungen erfolgen
kann. Bei Verwendung einer vorwärtsgekoppelten Topologie wird das
Ausgabesignal eines Neurons ausschliesslich an die nachgeschalteten
Neuronen weitergeleitet (vergleiche Abbildung 2.3a). Soll das Ausgabesignal
eines Neurons an jedes andere Neuron gesendet werden können, muss
eine rückwärtsgekoppelte Topologie implementiert werden. Im Falle
einer rückwärtsgekoppelten Topologie kann jedes Neuron sogar
das eigene Ausgabesignale als Eingabesignal wiederverwenden (vergleiche
Abbildung 2.3b).
Neuronale Netzwerke haben grundsätzlich die Aufgabe, eine gegebene Menge
von Eingabesignalen (Ist-Eingabemenge) auf eine bestimmte Menge von
Ausgabesignalen (Soll-Ausgabemenge) abzubilden. Die gewünschte
Langzeitdynamik des neuronalen Netzwerks wird durch die Spezifizierung der
Schichtstruktur, der Funktionsstruktur und der Gewichtestruktur erreicht. In Bezug
auf das Lernverfahren ist der letzte Punkt von Interesse, denn man kann die Gewichte
nur bei sehr einfachen neuronalen Netzwerken auf analytische Weise rechnerisch
konstruieren, weswegen man sie üblicherweise durch einen numerischen
Trainingsprozess bestimmen lässt. Dabei kommen verschiedene
Lernverfahren für neuronale Netzwerke zum Einsatz, die alle auf der
hebbschen Hypothese (1949) basieren:
Der Übertragungswiederstand einer Synapse (Gewicht) verändert sich
jedes Mal, wenn gleichzeitig vor und nach der Synapse eine neuronale
Aktivität besteht.
Ein neuronales Netzwerk "lernt", indem es in Abhängigkeit von
den eingespeisten Signalen die Verbindungsstruktur zwischen den Neuronen
ändert. Wie diese Modifikation während des Trainingsprozesses konkret
vor sich geht, wird in Abschnitt 3.2.3 anhand eines Lernverfahrens beschrieben,
welches auf dem Gradientenverfahren basiert. Allgemein gilt, dass
der Trainingsprozess so lange ausgeführt wird, bis ein
zufriedenstellendes Eingabe-Ausgabe-Verhalten des neuronalen Netzwerks erreicht
ist. Im normalen Arbeitsmodus findet dann keine Änderung der
Gewichte mehr statt.
Man unterscheidet zwei Kategorien von Lernverfahren:
-
Überwachte Lernverfahren: Hier werden die Ist-Ausgabesignale des
neuronalen Netzwerks nach jedem Schritt mit den zu erbringenden Soll-Ausgabesignalen
verglichen. Die Differenz wird jeweils zur Berechnung neuer Gewichtswerte benutzt,
die den Fehler auf der Ausgabeseite reduzieren, der durch eine sogenannte
Kostenfunktion ermittelt wird. In diese Kategorie ist auch das oben erwähnte
Gradientenverfahren einzuordnen.
-
Nicht-überwachte Lernverfahren: Diese Verfahren setzen
im Gegensatz zu den überwachten Lernverfahren keine Kenntnis der
Soll-Ausgabesignale voraus. Ein neuronales Netzwerk, welches auf diese Weise
trainiert wird, erkennt in den Eingabesignalen quasi selbstständig
Regelmässigkeiten. Die Gewichte können dadurch derart geändert
werden, dass ähnliche Eingabesignale gleiche Ausgabesignale produzieren.
Bei den nicht-überwachten Lernverfahren ist somit nur noch das Anspruchsniveau
der Abbruchkriterien durch Experten vorzugeben.